Basic Geometry

This is a short review of the geometric concepts and formulae that you will need for your Introductory Astronomy Course.

Contents:

1. Angles
2. Angles & Lines
3. Circles
4. Small Angle Formula
5. Angular Sizes

Angles

• Angles can be measured in different units. Usually we express them in degrees:

• Just as an hour can be divided into 60 minutes and a minute of time can be divided into 60 seconds, a degree can be divided into 60 arcminutes and an arcminute can be divided into 60 arcseconds:

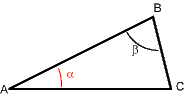
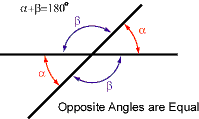
the angle labeled a can also be called Ð BAC, and the angle labeled b could also be called Ð ABC.

• Remember, there are 90° in a right angle

• There are a total of 180° in the three angles of a plane triangle: a + b + g = 180° :

• There are 360° in a circle:

Angles and Lines

• Where two lines cross 4 angles are created. Any two that are opposite eachother are equal, and any two that are adjacent sum to 180° .

• When two lines are parallel (such as AB and CD on the following figure), any line that crosses both of them (line EF) cuts off equal angles with the two parallel lines. Combined with the above rule, we see that all 4 angles marked in red below are equal.

Circles

Recall the definitions of the radius, diameter, and circumference of a circle:

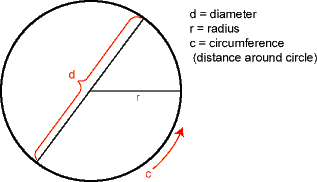
They are related by

with of course p = 3.14159…

The Small Angle Formula

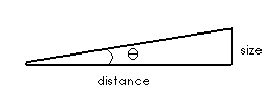
There is a very powerful formula relating the size of an object to its distance and its angular size. This formula, the small angle formula, comes from considering a circle of radius r. Remember that the circumference c is the distance all the way around the circle, and c=2p r. What if we are not interested in the distance all the way around the circle, but instead want to know the distance around part of the circle, say the length of the arc marked s?

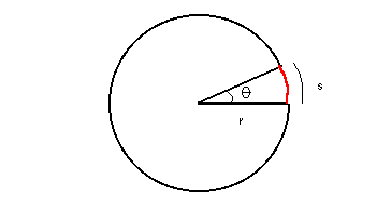
For this we can set up a ratio:

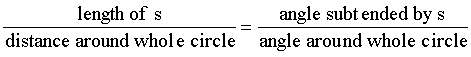
so that

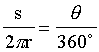
This is the small angle formula.

Why is this formula so great? Because it can even be used for things that are not part of a circle, as long as the angle is small! For example, when the angle is small (say less than 25), the triangle below looks an awful lot like the wedge from the circle above.

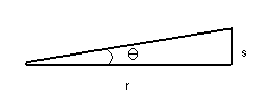
For this triangle, it is a good approximation to say that s, r, and are all related the small angle formula. Now we have a very powerful tool indeed, because we can turn a lot of astronomy problems into pictures involving skinny triangles…as you will see as you read on!

Angular Sizes

In astronomy, we study the universe while sitting comfortably here on good ol' Terra Firma. This means that we cannot generally measure the sizes of objects using rulers---let's face it, even if we were to visit Jupiter, it would be awfully hard to find a ruler big enough to measure it….

So from our earthly vantage point, we often describe the size of an object using an angular measure rather than a linear (ruler-like) one. If we are lucky enough to know something about an object's distance, then we can relate its angular size to its linear size using the small angle formula. This is a very frequent way of measuring things in astronomy.

As an example, imagine that you are looking at the Green Hall Tower from a distance of 200 meters. You estimate that from your point of view, the Tower covers an angle of 10°. We can draw the following picture:

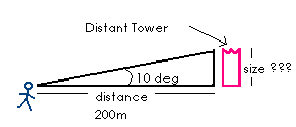
Note that this looks very similar to the skinny triangle picture above - in fact, we can apply the small angle formula to the triangle originating at your eyeball to get the height of the Tower:

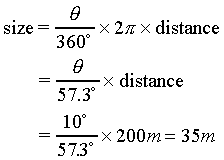
So we were able to measure the height of the Tower without actually going there!

The angle that an object covers when we trace it back to your eyeball is called its angular size. Consider the following pictures.

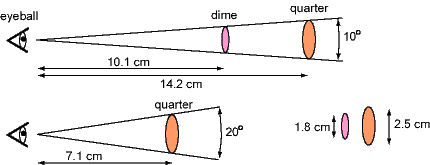
The top drawing demonstrates that two objects having different linear sizes can have the same angular size ( ) if they are viewed from different distances. The object's angular size is determined by the ratio size/distance. The quarter's linear size (2.5 cm) is 1.4 times as big as the dime's (1.8 cm) and so must be placed 1.4 times farther away to subtend the same angle. Now move the quarter two times closer as in the lower drawing, and its angular size is twice as big (20 degrees instead of 10 degrees).

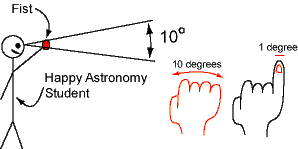
You can practice measuring the angular sizes of things (trees, constellations, friends) using various body parts! As shown in the picture below, the angular size of your fist when you put your arm straight out in front of you is approximately 10 degrees. Also with a straight arm, your pinky fingernail subtends about 1 degree.

Summary

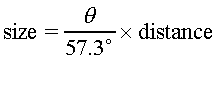
Note that you have to express the angle in degrees in order to get the units to work out properly. In astronomy we are often working with very small angles, measured in arcseconds. We can change the degrees in this equation to arcseconds using our units conversion methods:

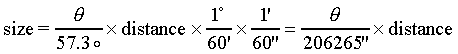
You will often see the small angle formula written in the textbooks in this form.

Practice

For practice, use the small angle formula and the concept of angular size to solve these problems:

1. Imagine you are watching a rocket launch from a distance of 3 km. The angular size of the rocket is 2 degrees. What is the length of the rocket in meters?
2. What is the angular size of the Moon and Sun as seen from Earth?  Use your textbook to find the diameter of and distances to the Moon and the Sun. Hint: your answer should be about the same in both cases!