Contents:
If you take your calculator and multiply 1.378 times 2.3 you will get 3.1694 as a result. If you divide 3.7 by 1.336 you will get 2.769461078. These results are "correct" in a pure mathematical sense that assumes you know the values of the initial numbers exactly. That is, that 3.7 is actually 3.7000000000..., that 1.378 is actually 1.378000000000... and so on. In the real world when we make measurements of anything, the value we get is not known exactly, but rather has some uncertainty associated with it. How large this uncertainty is depends to a high degree on the type of measuring device used as well as how it is used.
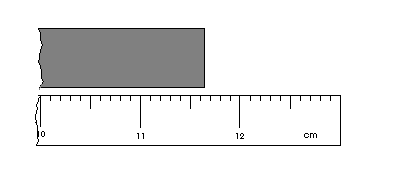
For example, suppose that three people were told to determine the length of a piece of wood and were given a tape measure whose smallest markings were at 0.1 centimeter intervals.

They report the following values:
Person |
Value measured for length |
|---|---|
1 |
11.6 cm |
2 |
11.6283476 cm |
3 |
11.63 cm |
Who is right? The correct question is "who has quoted a value of the proper accuracy?" Person 1 has been overly conservative because it is possible to estimate how far between the 0.1 cm marks the edge of the wood lies. Person 2 is being silly, because it is impossible to estimate such small distances by eye. Person 3 has made the best estimate of where the edge lies. No accuracy is lost as in case 1, and no unrealistic accuracy is claimed as in case 2. We’ve assumed here that one can measure accurately to one-tenth of the smallest markings on the ruler—in this case, that means to the nearest 0.01 cm. This example illustrates the general concept of significant figures (hereafter called S.F.) and the accuracy of the least significant digit (hereafter, uh, never mind).
So Person 3’s length measurement of 11.63 cm has 4 S.F., with the least significant digit in the hundredths place. Now Person 3 measures instead the width of the same piece of wood and finds it to be 5.74 cm. This result has the same accuracy as the previous measurement (both are given to the hundredths place), but only has three S.F. Similarly, her thickness measurement of 0.42 cm has the same accuracy but only two S.F.
The next sections will explain rules for determining how many S.F. are in a number and how many S.F to keep when you do calculations on numbers derived from measurements.
Here are a few rules to help you determine how many S.F. are in a given number, and which of the digits is the least significant one:
In any case, the least significant digit is then the significant digit that is farthest to the right. For our purposes, the accuracy of any quoted value can be assumed to be ± 1 of the least significant digit, unless stated otherwise.
Here are some examples to help you practice:
Sample Number |
# of S.F. |
Least Significant Digit |
Hints |
123.654 |
6 |
4 |
all digits are significant |
123.000 |
6 |
0 |
trailing zeros after decimal are significant |
0.000654 |
3 |
4 |
leading zeros are only placeholders |
100.32 |
5 |
2 |
middle zeros are always significant |
5400 |
? |
? |
don't know--are zeros placeholders? |
In the last case, we don’t know if the zeros are significant. If we knew the context, though, we could hopefully figure it out. For example, if you told me "I estimated the number of pollywogs in Paramecium Pond to be 5400± 100" then I’d know that the least significant digit is the 4, and the zeros are just placeholders. On the other hand, if you said "I banged my head in the pitch dark on that %@^$ (darn) telescope exactly 5400 times!" then I’d know that those zeros are significant.
As mentioned above, we cannot always take a number out of context and determine the number of S.F. For this reason (and also because scientists get tired of carrying around lots of zeros!) astronomers usually write numbers using scientific notation. When we convert a number to scientific notation, we get rid of any non-significant zeros. For our previous examples, we would write that the number of Paramecium Pond pollywogs is 5.4 x 103 (zeros were not significant so we dropped them), but that I banged my head 5.400 x 103 times (zeros were and are significant so we kept them).
In multiplication and division, the number of S.F. in the answer is the
same as the number of S.F. in the input number that has the fewest.
For example, consider Person 3's measurement of the wood. If you wanted to
know the area of the wood you would use the formula
Area = Length x Width
= (11.63
cm) x (5.74 cm)
The input number with the smallest number of S.F. is the width measurement,
which has 3. So, the answer must also have 3 S.F.:
Area = 66.8 cm2
The number that comes out of the calculator is 66.7562, but because of rule above the answer has been rounded off to the correct number of S.F.
Now suppose you wanted to know the volume of the wood:
Volume = Length x Width x Thickness
= (11.63 cm) x (5.74 cm) x (0.42 cm)
= 28 cm3
The calculator gives 28.037604, but because the thickness has only 2 S.F., so must the answer.
For addition and subtraction, the accuracy with which you quote an answer does not depend directly on the number of S.F. in the input numbers as above. Instead, it is determined by the position of the least significant digit in any of the input numbers. Here are some examples.
2.34 |
2.34 |
2.34 |
2.34 |
2.341234 |
|||||
+ |
0.18 |
+ |
2.8 |
- |
2.32 |
- |
8.43 |
- |
2.0 |
|
|
|
|
|
|||||
2.52 |
5.1 |
0.02 |
10.77 |
0.3 |
Note that the answer can have fewer, more, or the same number of S.F. as the various input numbers in the problem!