Unit Conversions

A common problem in astronomy is the conversion of a quantity measured in some units into a quantity based on other units. For example, we might know that Mars is 2 AU away from us, but need to know how many meters away it is. In everyday life similar situations arise: you are driving across Canada and need to change the 100 km per hr speed limit into more familiar miles per hour, or perhaps you are shopping at Price Club and need to compare the value of the 30 pound box of Corn Flakes with the 14 ounce box at your regular grocery store. In astronomy and elsewhere, you are almost guaranteed to get the wrong answer if you do not keep track of your units!

Let's start with the simple example of converting Mars' 2 AU distance into meters. Our problem is

.

We need to somehow get rid of the "AU" on the left and change it into meters. What we can find in the back of the textbook is an equation that says

(see the review of scientific notation if you are not familiar with this way of writing large numbers). The first step is to divide both sides by 1 AU, and notice that of course 1 AU divided by itself equals 1, so

.

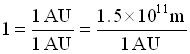Now if we take the distance to Mars of 2 AU and multiply it by 1, we don't change the distance. So we can write

.

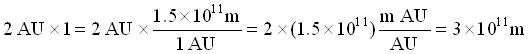Notice that we got rid of the "AU" by getting another "AU" on the bottom of the quantity, which allows us to cancel it out. And we are left with our quantity expressed in meters.

Next let's try a more complicated example: you are offered a full-time job paying $40,000 per year and another paying $12 per hour. Which should you take? Let's try to put these two salaries into the same units so we can compare them properly. Remember that "per" usually means "divided by", so the first salary is

.

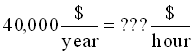Using our knowledge that 1 year=52 weeks and that a full-time job entails 40 hours in 1 week, we write

.

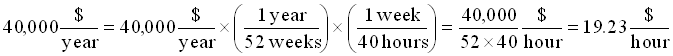Notice that the two quantities in parentheses are equal to one, so we can multiply by them whenever we want without changing the salary. Then note that the "year" and "week" units were made to cancel out. Obviously this is a better job than the one paying $12/hr.

Here is a more complicated example: How long would it take you to get to the Sun if you were to drive there in your car at 60 mph (miles per hour)?

First we remember that the equation for rates is

and since the problem is asking for the time, we divide both sides by the rate to get

.

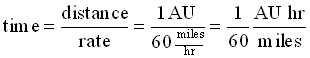So the right-hand side gives the answer, but in some strange units that we cannot understand. We would like to get rid of the AU and the miles-perhaps we could try to change both of them into meters so that they will cancel out. We look in our metric conversion table to find 1 mile=1.609 kilometers, and then write

.

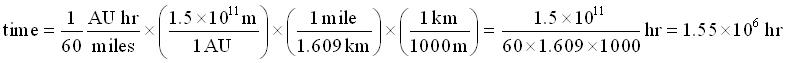Note how we constructed various versions of 1 to get rid of the AU, miles, and km, then the meters cancelled as well. The answer is not easy to comprehend, however - let's change the hours into years:

!

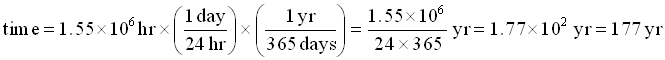Here is a list of useful conversions:

Length:

Angles:

Mass: