|
Outline - Two Dimensional Motion
|
- Vector and Scalar Quantities
- Scalar quantity possesses magnitude only.
Examples: speed, mass and temperature.
When you state a magnitude you give a number, e.g. 50 miles/hr.
- Vector quantities possess both magnitude and direction.
Examples: displacement velocity, acceleration, and force.
Magnitude and direction means, for example, 50 miles/hr, south.
- Two vectors are equal if they have the same magnitude and
direction. Moving a vector to a different location does not
change the vector as long as its direction and magnitude remain
constant.
- Usefulness of Vectors
- Principle of superposition: If an object is subjected
to two separate influences, each producing a characteristic
type of motion, it responds to each without modifying
its response to the other.
- A vector analysis allows you to separate two-dimensional
motion into two one-dimensional motions and then combine
them at the end of the problem. Example: projectile
motion.
- Rules for vector addition
- For vectors along a straight line use a positive sign
for a vector to the right and a negative sign for a vector
to the left.
- For vectors at an angle to each other use
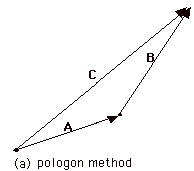
- The polygon method. In Fig. 1a, the vectors are
placed head to tail. The resultant vector goes from
the tail of the first vector A to the head
of the second vector B to give C = A
+ B.
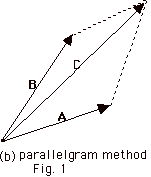
- The parallelogram method. Draw the vectors with
their tails at one point. Complete the parallelogram
and draw the diagonal to find the resultant.
Fig. 1b
- Cartesian coordinates
- Unit vectors. The unit vector i, j, and
k are unit vectors along the X, Y, and Z-axes,
respectively. When multiplied by a number or a symbol
that represents a quantity it becomes a vector with the
magnitude of the quantity (or symbol). For example, 5m
i is a vector of length 5 m along the X-axis.
- Components of vectors
- If a vector lies in the X-Y plane, it can be written
as a component in the X-direction added vectorally
to a component in the Y-direction. A= Axi
+ Ayj, where Ax and
Ay are the X and Y components of the vector
A (Fig. 2a).
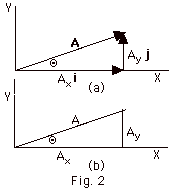
- From Fig. 2b, we see that Ax =
A cos Q, Ay
= A sin Q,
and A = (Ax2 + Ay2)1/2
- Utility of components. If two vectors are equal,
their components along any chosen axis are equal.
If C = D, then Cx =
Dx and Cy = Dy.
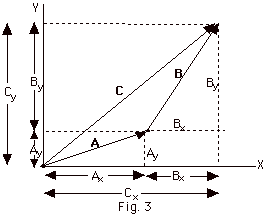
- Example (Fig. 3) A = Axi
+ Axj, and B = Bxi
+ Bxj
A + B = (Axi + Ayj)
+ (Bxi + Byj)
= (Ax + Bx)i + (Ay+
By)j
C = Cxi + Cxj
If C = A + B, Cx = (Ax
+ Bx) and Cy = (Ay+
By)
See Fig. 3
- Practice Problems in 104
Problem Set for Two Dimensional Motion:
1-4.
- Motion In Two-Dimensions
- Projectile Motion
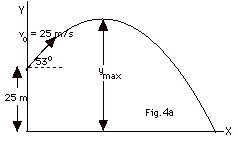
Sample problem:
An object is given an initial velocity of 25 m/s at an angle
of 53o with the horizontal. Find the initial position
of the object along (a) the X-axis, xo, and (b)
the Y axis, yo. Find the initial velocities
along (c) the X-axis, vox, and (d) the Y-axis,
voy. (e) Indicate the directions of vox
and voy on the figure. Find (f) the maximum vertical
height ymax, (g) the time for object to hit the
ground, (h) the distance x the projectile travels in a horizontal
direction, (i) vx, vy, and v just
before the object hits the ground, and (j) the angle
v makes with the horizontal. Take g = 10 m/s2.
Approach
to solution:
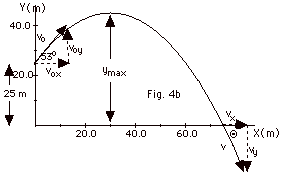
Choose an appropriate X and Y axis. For a projectile problem,
the appropriate X-axis is the horizontal direction and the
Y-axis the vertical direction. Draw the figure, as shown in
Fig. 4b below.
Set up a chart for the X and Y components of the descriptive
quantities. Identify the quantities asked for in (a) through
(d) of the statement of the problem along with the components
of the acceleration and enter them in the chart. Then write
appropriate formulae for the components of motion.
|
X
|
Y
|
|
(a) xo = 0
|
(b) yo =25 m
|
|
(c) vox = 25 m/s cos
53o
=15 m/s
|
(d) voy = 25 m/s sin
530
= 20 m/s
|
|
ax = 0
|
ay = -10 m/s2
|
|
x(t) = xo + voxt
+ 1/2 axt2
|
vy2(y)
= (voy)2 + 2ay(y
- yo)
|
|
(e) x(t) = 0 + 15 m/s t + 0
|
(f) At ymax, vy2(y)
= 0 =
(20m/s)2- 20m/s2(ymax-25m)
(ymax- 25 m) = 20 m, or
ymax = 45 m
|
| |
(g) y(t) = yo + voyt
+ 1/2 ayt2 when object hits
ground,
0 = 25 m + 20 m/s t - 5 m/s2 t2,
or t2-
4 s t - 5 s2 = 0
(t - 5 s)(t +1 s) = 0
t = 5 s. t cannot be negative.
|
|
(h) x(5s) = (15m/s)(5s) = 75m
|
|
|
(i) vx(t) = vox
+ axt
vx(5 s) = vox = 15m/s
|
(i) vy(t) = voy
+ ayt
vy(5 s) = 20 m/s -(10 m/s)(5s)
= -30 m/s
|
|
v = (vx2
+ vy2)1/2 = [152
+ (-30)2]1/2 m/s = 33.5m/s
|
|
(j) tan Q
= vy/vx = -30/15 = - 2.
Q = -63o
|
- Uniform Circular Motion
- An object has uniform circular motion when it moves
in a circle with constant speed. The speed v is constant,
but the velocity v is not constant, because v is always
tangent to the path so it continually changes direction.
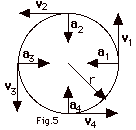
In Fig. 5 above, | v1|= |v2|=
|v3|= |v4|=
v, but this is not a case of constant velocity because
the direction of v changes.
- In Fig. 6 below, the two angles labeled Q
are equal because v2 and v1
are perpendicular to their respective radii.
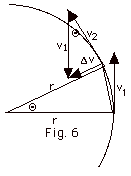
Since |v1|= |v2|=
v, the triangle with the radii and the
triangle with the velocities are similar because they
are isosceles triangles and they have angles that are
equal.
Thus Dv/v =
Dr/r or
Dv = Dr(v/r).
Divide both sides by Dt
and take limit as Dt
approaches zero:
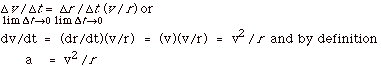
Since a = dv/dt, a has the
same direction as Dv,
or into the center of the circle.
- The magnitude of the acceleration is constant:
|a1|= |a2|=
|a3|= |a4|=
a = v2/r,
but this is not a case of constant acceleration because
the direction of a is not constant.
- Descriptive Terms
- Period T = time for one complete rotation = 2pr/v.
- Frequency f = number of revolutions per second
= the reciprocal of period = 1/T = v/2pr.
- The speed of the object = 2pr/T
= 2prf is a constant.
- Practice problems in 104
Problem Set for Two Dimensional Motion:
6-14.
|
|