Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 104

Outline - Simple Harmonic Motion
  1. Definition

    1. Simple harmonic motion occurs when the force F acting on an object is directly proportional to the displacement x of the object, but in the opposite direction.

    2. Mathematical statement F = -kx

    3. The force is called a restoring force because it always acts on the object to return it to its equilibrium position.


  2. Descriptive terms

    1. The amplitude A is the maximum displacement from the equilibrium position.

    2. The period T is the time for one complete oscillation. After time T the motion repeats itself. In general x(t) = x (t + T)

    3. The frequency f is the number of oscillations per second. The frequency equals the reciprocal of the period. f = 1/T.

    4. Although simple harmonic motion is not motion in a circle, it is convenient to use angular frequency by defining w = 2pf = 2p/T.


  3. Example of Simple Harmonic Motion - mass at end of spring

    A spring that obeys Hooke's Law is an example of simple harmonic motion. If you displace the spring a maximum amount x = A, the amplitude, release it from rest (vo = 0), photograph and plot the position as function of time, you find, as shown in Fig. 3a below that x(t) = A cos (2pt/T), where T, the period is the time for one complete oscillation.



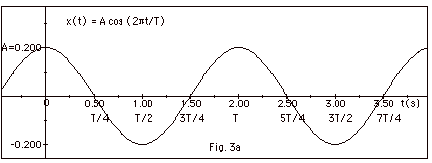
    To save time I shall write:

    x(t) = A cos (2pt/T), as
    x(t) = A cos wt

    then,

    v(t) = dx/dt = - wA sin wt,
    as shown in Fig. 3b below:



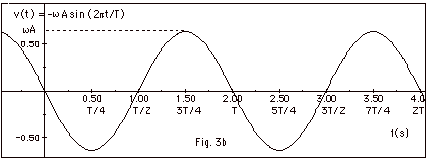
    Note: Maximum value of v = wA because maximum value of sine =1.
    a(t) = dv/dt = - w2 (A cos wt), as shown in Fig. 3c below:



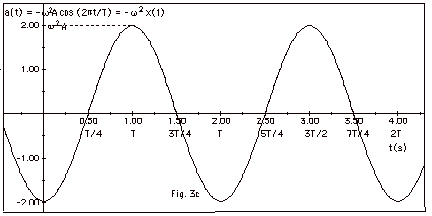
    Note: Maximum value of a = w2A because maximum value of cosine =1.
    a(t) = -[w2] x(t)   (Equation 2)

       In general,

    Fnet = ma

       For a mass attached to a spring,

    -kx = ma

       Substituting a from Equation 2

    -kx = m[-w2] x

       Thus,

    (k/m) = w2
     

    w = [k/m]1/2

     

    f = (1/2p)[k/m]1/2

     

    T = (2p) [m/k]1/2

    Use Fig. 3 above to:

    A. Write x(t) for this graph. First find A, T, f, and w. From Fig. 3a, you see that the maximum value of x or the amplitude A is 0.20 m. The graph repeats itself after one period = T = 2 s, f = 1/T = 0.5 s-1 and w = 2pf = p s-1. In general, x(t) = A cos wt. For this case x(t) = 0.20 m cos p s-1 t

    B. Find a general expression for the velocity, apply it to this case, and check with Fig. 3b to see if it is correct. What is the maximum value of the velocity for Fig. 3b? Find x when v = -0.1 p m/s. Since x(t) = 0.20 m cos p s-1 t, dx/dt = v(t) = -(0.20p m/s) sin p s-1 t. In Fig. 3b we see that v as a function of t is a negative sine curve with a maximum value of 0.2(3.14) m/s. v = -0.1p m/s
    = -(0.20p m/s) sin p s-1t. Or 1/2 = sin p s-1t. The sine of an angle is 1/2 when the angle is 300 or p/6 radians. So p/6 = p s-1t or t = 1/6 s. x(1/3 s)
    = 0.20 m cos p/6= 0.173 cm. From Fig. 3a and 3b, you can see that these are the correct values.

    C. Find a general expression for the acceleration, apply it to this case, and check with Fig. 3c to see if it is correct. What is the maximum value of the acceleration for Fig. 3b? Since v(t) = -(0.20p m/s) sin p s-1 t, dv/dt = a(t) =
    -(0.20p2 m/s) cos p s-1 t. In Fig. 3c we see that v as a function of t is a negative cosine curve with a maximum value of 0.2(3.14)2 m/s2 approximately
    equal to 2 m/s2.

    D. Sample Problems in 104 Problem Set for Simple Harmonic Motion: 1-6,
       10, and 12-16.



  4. Energy Considerations for Simple Harmonic Motion

    1. For all cases of simple harmonic motion, that is, when the force is directly proportional to the displacement of the object and in the opposite direction F = -kx, where k is the proportionality constant, the force is a conservative force and the potential energy function for this force is
      U = 1/2 kx2.

    2. The total energy E equals the sum of the potential energy U and the kinetic energy K: E = U + K          or  E = 1/2 kx 2 + 1/2 mv2

    3. When the object has a maximum displacement x = ±A, its velocity v is zero. E = 1/2 kA2 + 0 Since E is a constant, E always equals 1/2 kA2 for all times and displacements.

    4. When x = 0, U = 0 and E = 0 + 1/2 mv2. The maximum velocity of the object occurs at the equilibrium position.

    5. On the next page in Fig. 4, I have drawn the potential energy curve for the simple harmonic motion shown in Fig. 3. Find the spring constant k, the mass m of the object and check out the period of the motion.

    6. As you can see from Fig. 4, E is approximately equal to 0.20 J. In reality it is equal to 1/2(p2 N/m)(0.20 m)2 = 0.02p2 J = 1/2 kA2. Since A =
      0.20 m, k = p2 N/m. The maximum value of the velocity occurs at the equilibrium position. We found before that Vmax = wA = p s-1 (0.2 m) = 0.2p m/s. vmax2 = 0.04p2 m2/s2.  At the equilibrium position, the kinetic energy equals the total energy =1/2(p2 N/m)(0.20 m)2 = 1/2 mvmax2 =
      1/2 m 0.04p2 m2/s2 (1 N-s2/m) = 1 kg = m.

    7. Sample Problems in 104 Problem Set for Simple Harmonic Motion: 19, 20.

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
September 25, 2002
April 4, 2003