|
|
|
1.
|
Figure 1a below represents a wave at
t = 0 traveling along a rope to the right.
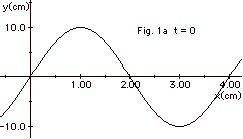
Figure 1b below represents the same wave at t = 10 s = a fraction
of the
period T.
Find (a) the wavelength of the wave, (b) the frequency of
the source that produces the wave, (c) the velocity of the
wave, (d) on an extension of the graph to the right, two other
positions where you expect to find crests at
t = 10 s, (e) at what later time there will be another crest
at x = 1 cm. (f) the number of times the displacement
of the rope is zero at x = 2.0 cm during each period, and
(g) the number of crests that pass x = 1.0 cm in 80 s.
|
|
|
2.
|
For the wave of Fig. 1, sketch a graph
of the displacement y as a function of time t for (a) x =
0, (b) x = 2.0 cm and (c) x = 4.0 cm from t = 0 to t = 20
s.
|
|
|
3.
|
a) In Fig. 1, is the point at x = 0 in
phase with the point at x = 2.0 cm? (b) Is it in phase with
the point at x = 4.0 cm?
|
|
|
4.
|
Write an equation for the wave of Fig.
1 that gives the displacement y as a function of x and t.
|
|
|
5.
|
Write an equation for y as a function
of t for the point at (a) x = 0 ,(b) x = 2.0 cm and (c) x
= 4.0 cm for the wave of Fig. 1.
|
|
|
6.
|
For x = 0, write an equation for the
transverse (a) velocity and (b) acceleration as a function
of time for the wave of Fig. 1.
|
|
|
7.
|
Illustrate, by drawing figures, (a) two
waves of the same amplitude but different wavelengths, and
(b) two waves of the same wavelength but different amplitudes.
|
|
|
8.
|
At t = 0 a wave traveling along a rope
to the right has a maximum displacement of +10 cm at x = 0.
The source that produces the wave makes 10 vibrations per
second. The velocity of the wave is 40 cm/s. Sketch the displacement
y of the rope as a function of the distance x along the rope
for (a) t = 0 and (b) t = 0.05 s. (c) Write an equation for y as a function
of x and t for this wave.
|
|
|
9.
|
The equation of a transverse traveling
wave on a string is y(x,t) =
2.0cm sin(0.50p cm-1x–200p
s-1 t) (a) Find the amplitude, wavelength, period,
frequency, velocity, and the direction of motion of the wave.
(b) Sketch the wave at the following values of t: 0,
0.0025 s, and 0.0050 s. (c) Find the transverse velocity
of the string at x = 1.0 cm at t = 0 and t = 0.0025 s.
|
|
|
10.
|
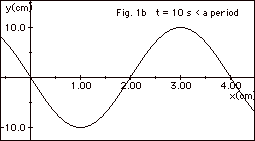
Fig. 2a below represents a wave at time
t = 0 traveling along a rope to the right and Fig. 2b a wave
along the same rope to the left, which together produce a
standing wave. (a) How far apart will crest C and crest C’
be at t = T/2, where T = the period? (b) Describe the resultant
displacement of the rope as a function of x at t = 3T/4.
|
|
 |
|
11.
|
Do points on a rope along which (a) a
traveling wave exists, (b) a standing wave exists, vibrate
up and down with simple harmonic motion? Do points on a rope
along which (c) a traveling wave exists, (d) a standing wave
exists, have the same amplitude? (c) How many times in one
period will the entire rope have zero displacement
for (e) a traveling wave? (f) a standing wave?
|
|
|
12.
|
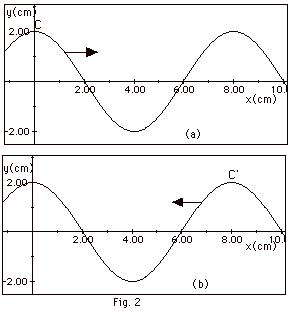
A wave travels along a rope to the right
in the +x-direction (there is no reflected wave). At time
t = 0, a plot of displacement y as a function of distance
x along the rope looks like Fig. 3a below. Sketch a graph
of displacement y as a function of x for t = -T/4, t = T/4,
and t = T/2, where T is the period of the wave.
|
|
 |
|
13.
|
Sketch a graph of the displacement y
of the rope for the wave of Problem 12 at x = 0, as a function
of time for the times given in #12.
|
|
|
14.
|
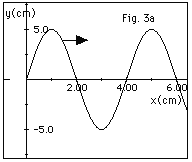
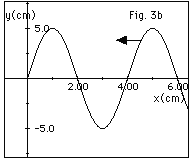
A wave travels along a rope to the left
in the -x-direction (there is no reflected wave). At time
t = 0, a plot of displacement y as a function of the distance
x along the rope looks like Fig. 3b below. Sketch a graph
of displacement y as a function of x for the times given in
#12.
|
|
 |
|
15.
|
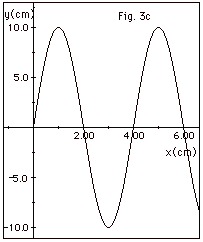
We now look at the rope for different
times due to the combined displacements by the waves of Fig.
3a and Fig. 3b. At time t = 0, a plot of the resultant displacement
y due to both waves versus position x for looks like Fig.
3c below. Sketch a graph of displacement y as a function of
x for the times given in #12.
|
|
|
| |
|
16.
|
Sketch a graph of the displacement of
the rope as a function of time at
x = 1.0 cm in Fig. 3c.
|
|
|
17.
|
The velocity of a wave along a string
depends only on the tension or force F exerted on the string
and the mass per unit length µ of the string. (a) From
a consideration of the units of the following quantities,
a dimensional analysis, decide which is the correct expression
for a wave along a string: (i) µ/F, (ii) Fµ,
(iii) (µ/F)1/2 or (iv) (F/µ)1/2.
(b) Standing waves are set up in a string by a vibrator of
frequency f. If the tension in the string is increased by
a factor of four, what happens to the number of nodal points?
|
|
|
18.
|
The equation of a transverse wave on
a string is:
y(x,t)
= 2.0 cm sin (2p cm-1
x – 600p s-1 t)
The tension in the string is 18 N. Find (a) the velocity
of the wave and (b) the mass per unit length of the string.
|
|
|
19.
|
A stretched string has a mass per unit
length of 4.0 x 10-3 kg/m and a tension of 1.6
N. A sinusoidal wave on this string has an amplitude of 1.0
cm and a frequency of 100 Hz and is traveling toward decreasing
x. Write an equation for this wave.
|
|
|
20.
|
A certain violin string is 50 cm long
between its fixed points. The string produces a note of A
(440 Hz) when played without fingering. Where must a finger
be placed to produce a note of C (528 Hz)?
|
|
|
21.
|
The lowest frequency of a stretched
string is 30 s-1 when the supports are 60 cm apart.
What is the speed of propagation of a wave in the string?
|
|
|
22.
|
Two birds sit on a telephone wire, as
shown in Fig. 4 below. The wire is rigidly attached to the
poles at A and B. A person at pole A wishes to dislodge bird
2 without disturbing bird 1. She sets up a standing wave with
a velocity of 48 m/s. (a) What is the longest wavelength that
will get the job done? (b) At what frequency should she shake
the wire in order to make such a wave? (c) If bird 2 can hold
on only if his up-and-down acceleration is less than 48 m/s2,
what is the smallest amplitude needed to dislodge bird 2?
|
|
 |
| 23. |
A string oscillates according to the
equation:
y(x, t) = 1.0 cm (sin px/3 cm-1)
cos 20p t s-1
Find (a) the amplitude, (b) the speed and (c) the equations
of the waves whose superposition gives this oscillation. Find
(d) the distance between nodes and (e) the speed of the particle
at x = 1.5 cm and t = 1/4 s.
|
|
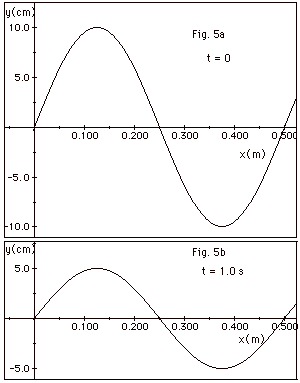
| 24. |
A standing wave is set up in a long rope.
At t = 0 the standing wave with maximum displacement of its
antinodes looks like Fig. 5a below. One second later (for
the first time) it looks like Fig. 5b. Find (a) the wavelength
and (b) the period of the wave. (c) If the total length of
the rope is 1.25 m, is the rope fixed at both ends, or is
it fixed at one end and free at the other? (d) Write the equation
of the standing wave. (e) What are the three longest wavelengths
for standing waves in the string? Sketch the corresponding
standing waves.
|
|
 |
| 25. |
What are the boundary conditions for
a string (a) fixed at x = 0 and x = L and (b) fixed at x =
0 and free at x = L? Explain the reasons for these conditions.
Use these conditions to find the allowed (c) wavelengths and
(d) frequencies for a string (i) fixed at x = 0 and x = L
and (ii) fixed at x = 0 and free at x = L.
|
|
| 26. |
An observer rides with a moving sound
source directly toward a large vertical wall. The vehicle
has a constant speed of 10.0 m/s and the source has a frequency
of 100 Hz. What beat frequency is heard by the observer due
to the combination of the direct and reflected sounds? Take
the velocity of sound to be 340.0 m/s.
|
|