|
|
|
1.
|
(a) From Figures 1a and 1b above, we
find the wavelength to be 4.00 cm.
(b) The crest at x = 1.00 cm in Fig. 1a moves to x = 3.00
cm in Fig. 1b in 10 s. Since the wave moves one wavelength
in a period T and (3.00 cm - 1.00 cm) is one-half wavelength,
the period is 20 s. The frequency f = 1/T = (1/20) s-1.
(c) v = fl = (1/20)
s-1 (4.00 cm) = 0.20 cm/s.
(d) At t = 10 s, there is a crest at x = 3.00 cm. There will
be two more crests at 3.00 cm + l
and 3.00 cm + 2l or at
x = 7.00 cm and x = 11.00 cm.
(e) At t = 0 there is a crest at x =1.00 cm. There will be
another crest at T =
20 s.
(f) The rope has zero displacement at any x twice each period.
(g) There is one crest at any point in one period. In 80 s
there will be 80/20 =
4 crests.
|
|
|
2.
|
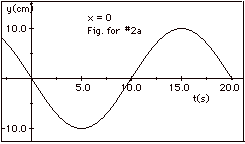
(a) In Fig. 1a above, for y = 0
at t = 0 and x = 0, you see a trough approaching
from the left. Similarly in Fig. 1b above, for y = 0
at t = 10 s and x = 0, you see a crest approaching
from the left. This is shown below in a plot of y as a function
of t for x = 0 (Fig. for #2a):
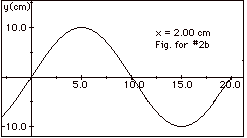
(b) In Fig. 1a above, for y = 0 at t = 0
and x = 2.00 cm, you see a crest approaching from the
left. A plot of y as a function of t for x = 2 cm is shown
in Fig. for #2b below:
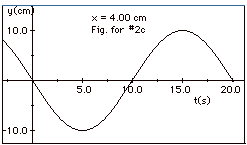
(c) In Fig. 1a, for y = 0 at t = 0 and
x = 4 cm, you see a trough approaching from the left. In Fig.
1b, for y = 0 at t = 10 s and
x = 4 cm, you see a crest approaching from the left. A plot
of y as a function of t for x = 4.0 cm is shown in fig. for
#2c below:
|
|
|
3.
|
The question is answered simply by looking
at Fig. for #2a through #2c above.There is no question that
Fig. for #2a is equivalent to #2c. Points are in phase when
they are an integral number of l's
apart. Points at x = 0 and x =
2 cm are l/2 apart and
are 1800 out of phase. Points at x = 0 and x =
4 cm are l apart and are
in phase.
|
|
|
4.
|
For a wave traveling to the
right, we may write
y(x,t) = ym sin (2px/
l - 2pt/T)
where ym is the amplitude of the wave, l
its wavelength, and T the period.
For this case ym = 10 cm, l
= 4.0 cm, T = 20 s, and
y(x,t) = 10 cm sin [(2px/4.0)cm-1
- (2pt/20)s-1]
= 10
cm sin [(px/2)cm-1
- (0.1pt)s-1]
|
|
|
5.
|
(a) For x = 0,
y(0,t) = 10 cm sin (-0.1pt
s-1)
= -10 cm
sin (0.1pt
s-1) as shown in Fig. for #2a above.
(b) For x = 2.0 cm,
y(2.0 cm, t) = 10 cm sin [(2p/2)
- (0.1pt)s-1]
=
10 cm{ sin p
cos 0.1pt
s-1 - cos p
sin 0.1pt
s-1}
=
10 cm{(0) cos 0.1pt
s-1 - (-1) sin 0.1pt
s-1}
=
10 cm sin 0.1pt
s-1 as shown in Fig. for
#2b above.
(c) For x = 4.0 cm,
y(4.0 cm, t) = 10 cm sin [(4p/2)
- (0.1pt)s-1]
=
10 cm{ sin 2p
cos 0.1pt
s-1 - cos 2psin
0.1pt
s-1}
=
10 cm{(0) cos 0.1pt
s-1 - (1) sin 0.1pt
s-1}
=
-10 cm sin 0.1pt
s-1
as shown in Fig. for #2c
above.
|
|
|
6.
|
For x = 0, y(0,t) = -10 cm sin (0.1pt
s-1):
(a) v(0, t) = dx/dt = -1.0p
cm/s cos (0.1pt s-1)
(b) a(0,t) = dv/dt = +0.1p2
cm/s2 sin (0.1pt
s-1) = -(0.1p2
s-2)y(0,t)
|
|
|
7.
|
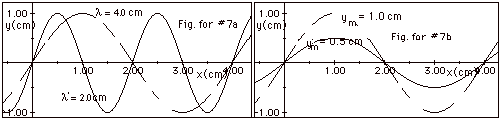
Dashed
wave: l = 4.0 cm: solid: l’
= 2.0 cm.
Dashed wave: ym = 1.0 cm; solid: ym’
= 0.5 cm
(a) Two waves of the same amplitude, but different wavelengths
(Fig. for #7a).
(b) Two waves of the same wavelength, but different amplitudes
(Fig. for #7b).
|
|
|
8.
|
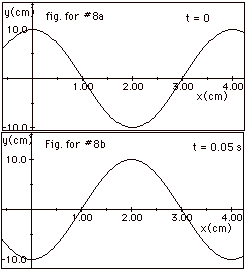
Since y has a maximum displacement of 10 cm at x = 0, we use
a cosine function for the wave of amplitude xm =
10 cm. With a frequency f of 10 s-1 and a velocity
v = 40 cm/s, l = v/f
= 40 cm/s/10 s-1 = 4.0 cm.
(a) A plot of y as a function of x for t = 0 is shown in Fig.
for #8a above. Notice the maximum displacement of 10 cm for
x = 0 and the wavelength of the wave as 4.0 cm.
(b) For f = 10 s-1, T = 1/f = 0.10 s. A plot of y
as a function of x for t = 0.05 s
= T/2 is shown in Fig. for #8b above. Notice that the crest
at x = 0 for t = 0 has moved to x = 2.0 cm = l/2
in time T/2. In general for a wave moving to the right,
y(x,t) = ym cos(2px/ l
- 2pt/T)
For this wave,
y(x,t) = 10 cm cos [(px/2)cm-1
- (20pt)s-1]
|
|
|
9.
|
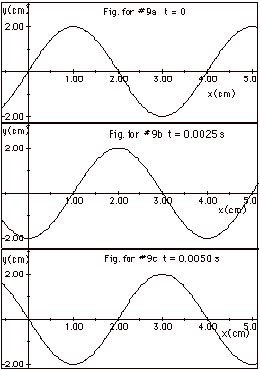
(a) In general, y(x,t) = ym sin (2px/ l
- 2pt/t)
for a wave to the right. For our case, y(x,t) = 2.0 cm sin (0.50p
cm-1x - 200p
s-1t). By comparison, ym = 2.0 cm; 2p/ l
= 0.50p cm-1,
or l = 4.0 cm; 2p/T
= 200p s-1, or
T = 0.01 s; frequency f = 1/T = 100 s-1; v = lf
= (4.0 cm)(100 s-1) = 40 cm/s; direction of the wave
is to the right because of - sign in wave equation.
(b) There is a crest at x =1.00 cm at t = 0 (Fig. for #9a above).
This crest moves to the right to x = 2.00 cm or a distance of
1.00 cm = l/4 in time 0.0025s
= T/4 (Fig. for #9b above). The crests moves to the right to
x = 3.00 cm or a distance of 2.00 cm = l/2
in time 0.0050 s = T/2 (Fig. for #9c above).
(c) y(x, t) = 2.0 cm sin(0.5p
cm-1x-200ps-1t).
(dy/dt)x =1cm = -400p
cm/s cos(0.5p -200ps-1t).
(dy/dt)x=1cm,t=0 = -400p
cm/s cos 0.5p
= 0.
(dy/dt)x=1cm,t = 0.0025s = -400p
cm/s cos(0.5p - 0.5p)
= -400p cm/s.
|
|
|
10.
|
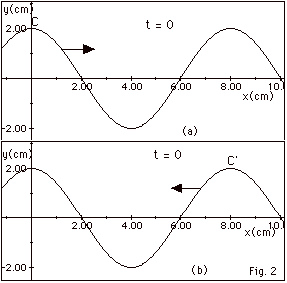
A wave moves one wavelength in one period. From Figs. 2a and
2b above, we see that the wavelength of the waves = 8.0 cm
. In one-half period the waves moves 4.0 cm. Crest C, on the
wave that is moving to the right, at x = 0 in Fig. 2a, moves
to x = 4.0 cm in T/2. Crest C’, on the wave that is
moving to the left, at x = 8.0 cm in Fig. 2b, moves to x =
4.0 cm. At t = T/2, there will be a double crest at x = 4.0
cm with a displacement y = 4.00 cm.
The individual waves to the right and
to the left, respectively, are shown immediately above in
Fig for #10 (b) at t = 3T/4. Now C has moved to the right
3l/4 = 6.0 cm to x = 6.0
cm and C’ has moved 6.0 cm to the left to x = 2.0 cm.
C at x = 6.0 cm is superimposed with a trough at this point
from the wave moving to the left. C’ at x = 2.0
cm is superimposed with a trough at this point from the wave
moving to the right. The entire string has zero displacement
at
t = 3T/4.
|
|
|
11.
|
(a) Points on a rope along which a traveling
wave exists vibrate up and down with simple harmonic motion.
(b) All point on the rope except the nodal points on a rope
along which a standing wave exists vibrate up and down with
simple harmonic motion.
(c) All points on a rope along which a traveling wave exits
vibrate with the same amplitude.
(d) The amplitude of a rope along which a standing wave exists
varies from a maximum at the antinodes to zero at the nodes.
(e) The entire rope along which a traveling wave exits never
has zero displacement.
(f) The entire rope along which a standing wave exists has
zero displacement twice each period.
|
|
|
12.
|
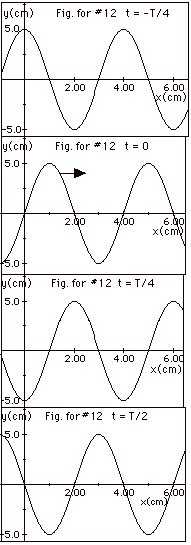
The plots are shown in Fig. for #12 below
for a wave traveling to the right.
The wavelength of the wave is 4.0 cm. The crest at x = 0 at
-T/4 moves to
x = 1.0 cm at t = 0; to x = 2.0 cm at t = T/4, and to x =
3.0 cm at t = T/2.
|
|
|
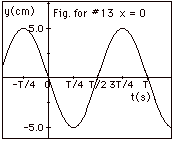
13.
|
|
The plot of y vs t for x = 0 is
shown to the right in Fig for #13. If you look above
at the graphs for Fig. for #12, you see that the point
at x = 0 has the following values of y:
y = 5.0 cm at t =-T/4, y = 0 at t = 0,
y = 5.0 cm at t = T/4, and y = 0 at t = T/2.
|
 |
|
|
|
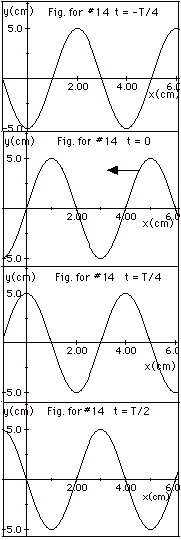
14.
|
The plots are shown in the graphs below
in Fig. for #14 for a wave traveling to the left. The crest
at x = 6 cm at t = -T/4 moves l/4
= 1 cm to x = 5 cm at t = 0; to x = 4 cm at x = T/4, and to
x = 3 cm at x = T/2.
|
|
|
15.
|
If you look back at the graphs for Fig.
for #12 and Fig. for #14, above, and add the displacement
y for various values of x for t = -T/4, t = 0, t = T/4, and
t = T/2, you will get the graphs shown below in Fig. for #15.
At times t = -T/4 and
t = T/4, the entire rope has zero displacement.
|
|
|
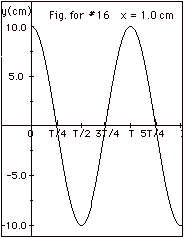
16.
|
The point on the rope at x = 1.0 cm is
an antinodal point. If you look above at the Fig. for
#15 you see the point at x = 1.0 cm has y = 10 cm at t = 0,
y = 0 at t = T/4, and y = -10 cm at T/2. These correspond
to the values of y as a function of time shown in the Fig.
for #16 below. The amplitude of an antinodal point varies
from 0 to a maximum, in this case, 10 cm.
|
|
|
17.
|
(a) The unit of force is N or kg-m/s2.
The unit of mass per unit length µ is kg/m, the unit of
velocity v is m/s.
- The unit of µ/F is (kg/m)/(kg-m/s2) =
(s/m)2 ≠ m/s.
- The unit of F/µ is (kg-m/s2)/(kg/m) =
(m/s)2 ≠ m/s. We could stop here and write
down the answer, but let's carry on.
- The unit of (µ/F)1/2 = s/m ≠ m/s.
- The unit of (F/µ)1/2 = m/s!
(b) The distance between nodes is l/2.
Thus the number of nodes is inverserly proportional to l.
lf = v. The velocity
v is directly proportional to the square root of the tension
F. If the tension is increased by a factor of four, the square
root of the tension and the velocity is increased by a factor
of two. For a fixed frequency f, the wavelength is directly
proportional to the velocity v. If the velocity is doubled,
the wavelength is doubled. If the wavelength is doubled, the
number of nodes, which is inversely proportional to the wavelength,
is halved. |
|
|
18.
|
In general for a wave to the left, y(x,t)
= ym sin (2px/ l
- 2pt/T). When we compare
y(x,t) = 2.0 cm sin (2px
cm-1 - 600pt
s-1), you see that 2p/l
=
2p cm-1, or
l= 1.0 cm. Also
2p/T = 600p
s-1, or T = (1/300) s and
f= 1/T = 300 s-1.
(a) v = lf = 1.0 cm(300
s-1) = 300 cm/s.
(b) v = (F/µ)1/2, or v2 =
F/µ.
µ = F/v2 = 18 N/(3 X 102
m/s)2 = 2 x 10-4 (kg-m/s2/m2/s2)
= 2 x 10-4 kg/m.
|
|
|
19.
|
To find the equation of a wave, we must
find the amplitude A, wavelength l,
and frequency f of the wave. We are given ym =
1.0 cm and f = 100 s-1, the tension in the
string F = 1.6 N, the mass per unit length µ =
4.0 x 10-3 kg/m. We know that l
= v/f and v = (F/µ)1/2 = (1.6 N/4.0 x10-3
kg/m)1/2 = 20 m/s. Then l
= v/f = 20 m/s/100 s-1 = 0.20 m = 20 cm. The
wave is going toward smaller values of x, or to the left.
For a wave to the left, y(x,t) = ym sin (2px/ l
+ 2pft).
For our case, y(x,t) = 1.0 cm sin (0.10px
cm-1 + 200pt
s-1).
|
|
|
20.
|
For a string fixed at both ends, the
allowed frequencies are fn = nv/2L, where
n is an integer, v the velocity, and L the length of the string.
For f = 440 s-1 and L = 50 cm, nv =
2fnL = 2(440 s-1)50 cm = 4.4 x 104
cm/s. For a frequency of
528 s-1 = nv/2L’ = 4.4 x 104 cm/s/2L’
or L’ = 2.2 x 104 cm/528 = 41.7 cm.
|
|
|
21.
|
The lowest frequency occurs for n = 1
in fn = nv/2L.
30 s-1 = v/2(60 cm); v = 3.6 x 103
cm/s.
|
|
|
22.
|
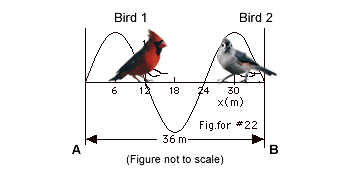
(a) To dislodge bird 2 without disturbing bird 1, she needs
an antinode at the position of bird 2 and a node at the position
of bird 1. With a node at both ends of the wire, the longest
wavelength is in the Fig. for #22 above. From the figure,
3l/2 = 36 cm, l
= 24 cm.
(b) f = v/ l = 48
m/s/24 m = 2 s-1.
(c) For a standing wave, y(x,t) = ym sin
2px/ l
cos 2pft.
dy/dt = -2p
ym sin 2px/ l
sin 2pft.
a = d2y/dt2
= -(2pf)2
ym sin 2px/ l
cos 2pft.
The maximum value of the sine and cosine is 1. If the maximum
absolute value of the acceleration bird 2 can withstand is
48 m/s2, then 48 m/s2 = (2pf)2ymax,
where ymax is the maximum amplitude he can
withstand.
ymax = 48 m/s2/(4ps-1)2
= 0.30m. Any amplitude slightly greater than this
is the smallest amplitude needed to dislodge the bird.
|
|
|
23.
|
General equation for a standing wave
is
y(x,t) = ym sin 2px/ l
cos 2pft
Compare this with y(x,t) = 1.0 cm (sin px/3 cm-1)
cos 20pt s-1 to find that
(a) A = 1.0 cm,
(b) 2pl
= p/3 cm-1
or l =
6 cm, 2pf = 20p
s-1 or f = 10 s-1
and v =
lf = 6 cm(10 s-1) = 60 cm/s.
(c) We need two waves of the same wavelength and
frequency, traveling in opposite
directions with an amplitude = 0.5 cm.
y1(x,t) = 0.5 cm
sin (px/3 cm-1 -
20pt s-1) and
y2(x,t) =
0.5 cm sin (px/3
cm-1 + 20pt
s-1).
(d) the distance between nodes =
l/2 = 3.0 cm.
(e) v(x,t) = dx/dt = -20 p
cm/s sin px/3 cm-1
sin 20pt s-1.
v(1.5 cm, 1/4 s) = -20p
cm/s (sin p/2) (sin 5p)
= -20p(1)(0) = 0.
|
|
|
24.
|
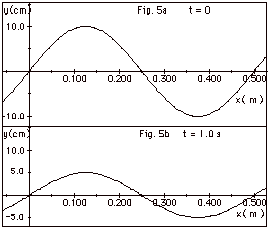
(a) Distance between nodes = l/2
= 0.250 m. l = 0.500
m.
(b) For an antinodal point, y(t) = 10.0 cos 2pt/T.
For t = 1.0 s, 5.0 cm =10.0
cos 2p s/T.
cos-1 0.50 = p/6
= 2p s/T.
T = 12 s.
(c) # of half wavelengths in 1.25 m = 1.25 m/0.25 m = 5. There
is a node at both ends. The
rope is fixed at both ends.
(d) Now y(x,t) = A sin 2px/l
cos 2pft = 10 cm sin 4px
cm-1 cos pt
s-1/6
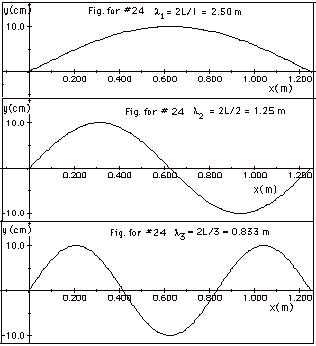
(e) ln =
2L/n. For n = 1, l1
= 2L = 2(1.25 m) = 2.50 m. For n = 2, l2
= L =
1.25 m. For n = 3, l3
= 2.50 m/3 = 0.833 m. The figures are shown below in
Fig. for #24.
|
|
|
25.
|
For a standing wave, y(x,t) = ym
sin 2px/ l
cos 2pft. The end at which
a string is fixed must have a node or y = 0 at that end. For
a string fixed at x = 0, this expression gives y(0,t) = 0.
For a string also fixed at L, y(L,t) = 0 =
ym sin 2pL/ l
cos2pft. For this
to be 0, sin 2pL/ l
= 0 or 2pL/ l
= np and ln
= 2L/n, where n = 1, 2, 3, . . . For a string
fixed at x = 0, you still use the sine, but now with the string
no longer fixed at L you want an antinode at x = L, or
dy/dx = 0 at x = L. dy/dx = 2pym/ l
cos 2px/ lcos
2pft. This will be zero
at all times at x = L if cos 2pL/ l
= 0 or 2pL/ l
= (n - 1/2) p and
ln = 2L/(n
- 1/2) with n = 1, 2, . .
|
|
|
26.
|
Consider an observer at the wall. For
her, the velocity of the source is vs = u and her
own velocity is zero. The frequency heard by the observer at
the wall is,
nwall
= no[v/(v-u)] (Equation
1)
The reflected sound now comes from a stationary source and is
heard by the moving observer. The frequency heard by the moving
observer is
n = nwall
[(v + u)/(v)] (Equation
2)
Substituting nwall
from Eq. 1 into Eq. 2:
n =
no[(v + u)/(v - u)]
The beat frequency is
n - no
= no[(v + u)/v
- u) - 1] = no [2u/(v
- u)]
= 100 Hz[2(10 m/s)/(340 - 10 m/s)] = = 6.1 Hz
|
|
|