Review - One Dimensional Motion

1.

An object moves with a constant velocity of 15 m/s. (a) How far will it travel in 2.0 s? (b) If the time is doubled, how far will it travel?

2.

An object, initially at rest, moves with a constant acceleration of 10 m/s². How far will it travel in (a) 2.0 s and (b) 4.0 s? If this object had an initial velocity of
4 m/s, how far will it travel in (c) 2.0 s and (d) 4.0 s?

3.

(a) An object moving with constant acceleration changes its speed from 20 m/s to 60 m/s in 2.0 s. What is the acceleration? (b) How far did it move in this time?

4.

An object moving with constant acceleration along a horizontal path covers the distance between two points 60 m apart in 6.0 s. Its speed as it passes the second point is 15 m/s. Find (a) the speed at the first point, (b) its acceleration and (c) the distance from the point where the object was at rest to the first point.

5.

A ball thrown straight up takes 2.0 s to reach a height of 40 m. Find (a) its initial speed, (b) its speed at this height, and (c) how much higher the ball will go. Take g = 10 m/s².

6.

A ball is thrown down vertically with an initial speed of 20 m/s from a height of 60 m. Find (a) its speed just before it strikes the ground and (b) how long it takes for the ball to reach the ground. Repeat (a) and (b) for the ball thrown directly up from the same height and with the same initial speed.
Take g = 10 m/s².

7.

A multiple choice question. (a) By definition, velocity equals the change in position divided by the time to change the position. The instantaneous velocity v = dx/dt is (i) the slope of the position x versus time t at any instant, (ii) the area under the x versus t curve up to that instant, (iii) the slope of the acceleration a versus time t at any instant. (b) Since v = dx/dt, by separation of variables dx = v dt or ∫dx = ∫v dt. Thus the distance moved in time t is (i) the slope of the velocity v versus time t at any instant (ii) the area under the velocity v versus time t curve up to time t (iii) the area under the acceleration a versus time t curve up to time t. (c) By definition, instantaneous acceleration a = dv/dt or (i) the slope of the position x versus time t at any instant, (ii) the slope of the velocity v versus time t at any instant, (ii) the area under the velocity v versus time t curve up to time t. (d) Since a = dv/dt, by separation of variables dv = a dt or ∫dv = ∫a dt. Thus the change in velocity up to time t is (i) the slope of the velocity v versus time t at any instant, (ii) the area under the velocity v versus time t curve up to time t, (iii) the area under the acceleration a versus time t curve up to time t.

8.

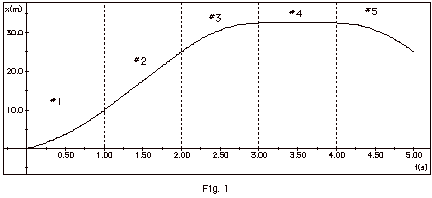
Figure 1 below is a plot of the displacement x of an object as a function of time t. The dashed vertical lines separate the one second intervals. During the first time interval #1 (t = 0 to t = 1 s) of Fig. 1 decide if the velocity of the object is (a) zero (b) constant and positive, (c) constant and negative, (d) increasing and positive, (e) increasing and negative, (f) decreasing and positive, or (g) decreasing and negative. (You may use a ruler to check the slopes of x vs t for the various time intervals.) Also decide for the same intervals if the acceleration is (note do not fix on one point in an interval) (h) positive (i) negative (j) zero. Explain your answers. Repeat the above for the other four time intervals in Figure 1.

9.

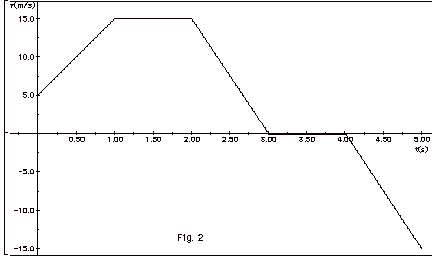
Figure 2 below shows the velocity of a particle as a function of time. (a) Find the acceleration for the five one-second periods and plot the acceleration as a function of time. (b) Taking x = 0 at t = 0, find the position of the particle at t = 0.5 s, t = 1.0 s, t = 2.0 s, t = 3.0 s, t = 4.0 s, and t = 5.0 s and plot the position as a function of time. Look at the slopes of your x vs t curve for the five one-second periods and show that they correspond to the velocities of Fig. 2.

10.

An object moving with a velocity of 10 m/s is uniformly decelerated, coming to rest in a distance of 20 m. Find (a) its deceleration and (b) the time for it to come to rest. Plot (c) its velocity v as a function of time t and (d) its position x as a function of t. Take x_o = 10 m.

11.

An apartment dweller sees a flower pot (originally on a window sill above) pass the 2.0-m-high window of her fifth floor apartment in 0.10 s. The distance between floors is 4.0 m. From which floor did the pot fall?

12.

The acceleration of a particle is given by a(t) = 6.0 m/s³ t. Find (a) v(t) and
(b) x(t) for a particle with v_o = x_o = 0.

13.

Repeat Problem 12 for v_o = 1.0 m/s and x_o = 2.0 m.

14.

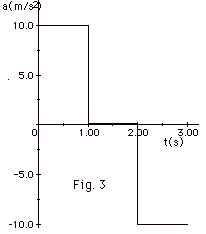
A particle starts from rest and undergoes accelerations as plotted in Fig. 3 below for the first three seconds. Plot a graph of (a) velocity v as a function of time t and (b) position x as a function of time t taking x_o = 0. Find (c) the maximum velocity during the period and (d) the distance moved by the particle in 3.0 s.

15.

At a certain instant, a ball is thrown downward with a velocity of 8.0 m/s from a height of 40 m. At the same instant, another ball is thrown upward from ground level directly in line with the first ball with a velocity of 12 m/s. Find (a) the time when the balls collide, (b) the height at which they collide, and (c) the direction the second ball is traveling when they collide. Take g = 10 m/s².

16.

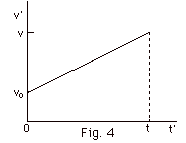
Use Fig. 4 below and geometry to find (a) the average velocity of the particle in time t and (b) the time at which the velocity of the particle equals the average velocity.

17.

Sketch a graph that is a possible description of position as a function of time for a particle that moves along the x axis and, at t = 1 s, has (a) zero velocity and positive acceleration; (b) zero velocity and negative acceleration; (c) negative velocity and positive acceleration; (d) negative velocity and negative acceleration. (e) For which of these situations is the speed of the particle increasing at t = 1 s?