|
Review - Simple Harmonic Motion
|
|
|
1.
|
Imagine that you video tape the motion
of a mass attached to a spring and measure the displacement
x from the equilibrium position as a function of time t. When
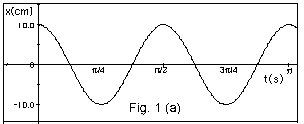
you plot x versus t, you get a graph resembling Fig. 1a below.
The mathematical expression for the curve of Fig. 1a is:
x(t) = A cos 2pt/T
(Equation
1)
where A is the amplitude of the motion, the maximum displacement
from the equilibrium position and T is the period, the time
for one complete oscillation. From Fig. 1a, find the amplitude
and the period of the motion.
 |
|
|
2.
|
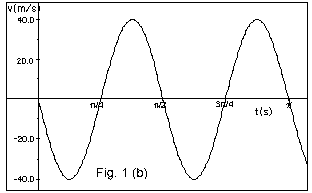
Fig. 1b below is a plot of the velocity
v as a function of the time t. You find v from the slope dx/dt
of x versus t.
v(t) = -2p/T(A
sin 2pt/T) (Equation
2)
Find (a) from Eq. 2 an expression for the maximum velocity
in symbols and (b) from Fig. 1b the magnitude of the maximum
velocity.
|
|
|
3.
|
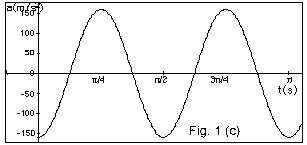
Fig. 1c below is a plot of acceleration
a as a function of the time t. You find a from the slope dv/dt
of v versus t.
a(t) = -(2pT)2
(A cos 2pt/T)
(Equation
3)
Find (a) from Eq. 3 (i) an expression for the maximum acceleration
and
(ii) -a(t)/x(t) in symbols and (b) from Fig. 1c the magnitude
of the maximum acceleration.
|
|
|
4.
|
When the force on an object is directly
proportional to, and in the opposite direction of, the displacement,
the motion of the object is simple harmonic. (a) Show that
the motion of a mass attached to a stretched spring is simple
harmonic. (b) Find the ratio, -acceleration/displacement.
(c) Equate the expression found for -a/x in Part b to that
found in Problem 3a(ii) to find the period T of the motion
for the mass-spring system.
|
|
|
5.
|
For x(t) = A cos 2pt/T,
xo = A when t = 0.
Since v(t) = -2p/T(A sin
2pt/T), vo
= 0.
In other words for this equation, the initial position xo
equals the maximum displacement A from the equilibrium
position and the initial velocity vo = 0. You can
provide for xo ≠ A and vo ≠
0 by writing:
x(t) = A cos (2pt/T+
d)
(Equation
1')
where d is the phase constant
that depends on xo and vo. Show that Equation
1' guarantees the definition of (a) the period T and (b)
the amplitude A. (c) Find xo and vo when
d = -p/2
and describe where the mass is initially and how it is moving.
|
|
|
6.
|
A massless spring with constant k exerts
a force on a mass m when the spring is extended a distance
x. By Newton’s second law of motion, -kx = ma. Since
the acceleration a = dv/dt = d/dt(dx/dt) = d2x/dt2,
-kx = m d2x/dt2 or
d2x/dt2 + (k/m)x = 0 (Equation
1")
Show that
x(t) = A cos (2pt/T +
d) (Equation
1')
is a solution to Eq. 1" if T = 2p(m/k)1/2.
Hint: find d2x/dt2 and substitute
it into Eq. 1'.
|
|
|
7.
|
Given x(t) = A cos (2pt/T
+ d). Sketch x(t) for
d equal to (a) 0, (b)
-p/2, and
(c) -p. Sketch v(t) for d equal
to (d) 0, (e) -p/2, and
(f) -p. (g) What is the
function of d?
|
|
|
8.
|
Given that x(t) = A cos (wt
+ d) find (a) x(0) = xo
and (b) v(0) = vo. Find in terms of xo,
vo, and w
= 2pn = 2pT (c)
tan d and (d) A.
|
|
|
9.
|
A massless spring of constant k is hung
vertically and not extended. A mass m is attached to the spring
and it stretches a distance xo. (a) Find
xo in terms of k, m and g. Now the spring is pulled
down an additional distance x. (b) Write Newton’s second
law for total extension (x + xo), and (c) find
the frequency of the motion when the spring is released.
|
|
|
10.
|
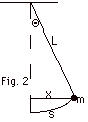
A pendulum
bob of mass m attached to a string of length L vibrates back
and forth along a circular arc. (a) Draw an isolation diagram
for the bob and show all the forces acting on it. (b) Write
Newton's second law of motion for the component of the force
tangent to the path. (c) For small angles, the horizontal
displacement x is approximately equal to the displacement
along the arc s (Fig. 2 below). Show that for small displacements,
the pendulum vibrates with simple harmonic motion. Find the
frequency of its motion.
|
|
|
11.
|
Given x(t) = 0.01 m cos (0.02p
s-1 t - p/2).
Find (a) the amplitude, (b) the period, (c) the frequency,
and (d) the initial phase of the motion.
|
|
|
12.
|
A particle is executing simple harmonic
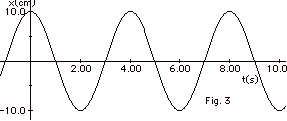
motion. The displacement x as a function of time t is shown
in Fig. 3 below. Find (a) the period, (b) amplitude,
(c) equation of motion, (d) maximum velocity and (e) maximum
acceleration.
|
|
|
13.
|
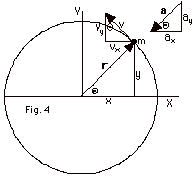
Figure 4 below represents a particle
of mass m moving with uniform circular motion. Find the following
components of r and a in the X-direction : (a)
displacement x and (b) the acceleration ax in terms
of r and a function of Q
= wt. (c) Find the ratio
of the acceleration -ax to the displacement x.
(d) Given that w = 2pf,
where f is the frequency of the motion, express the ratio
found (c) in terms of w.
(e) Is the projection of uniform circular motion on the X-axis
a case of simple harmonic motion? (f) Use your results from
(d) and Problem #4 to express the frequency f, the number
of oscillations per second, in terms of the mass m and spring
constant k. Repeat the above for the components of r
and a in the Y-direction.
|
|
|
14.
|
The x coordinate of a particle obeys
the equation b2 d2x/dt2 +
c2x = 0, where b and c are constants. What is the
period of oscillation?
|
|
|
15.
|
A pendulum bob swings a total distance
of 4.0 cm from end to end and reaches a speed of 10 cm/s at
the midpoint. Find the period of oscillation.
|
|
|
16.
|
The motion of a particle is given by
x(t) = 4.0 cm cos (pt
s-1 - p/6).
Find the velocity of the particle when x = 2.0 cm.
|
|
|
17.
|
A mass-spring system has frequency of
3/2 s-1. Find A and d
for
x(t) = A cos(pt + d)
if xo = 0.25 m and vo = -1.5 m/s.
|
|
|
18.
|
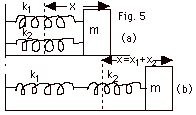
In
Fig. 5a below, two springs of spring constants k1
and k2 are connected in parallel. In Fig. 5b below,
they are connected in series. Find the frequencies of the
systems for (a) Fig. 5a and (b) Fig. 5b.
|
|
|
19.
|
A massless spring with spring constant
k = 10.0 N/m is attached to an object of mass m = 0.300 kg.
One third of the spring is cut off. What is the frequency
of the oscillations when the “new” spring-mass
is set into motion?
|
|
|
20.
|
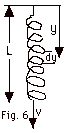
We wish to find the fraction of the mass
ms of a spring that contributes to the load when
a system is vibrating given that the kinetic energy of an
object of mass m and velocity v is given by K = 1/2 mv2.
For Fig. 6 below, find (a) the differential mass dm
of the spring of length dy, (b) the velocity of the element
assuming that the velocity varies linearly from v at y = L
to 0 at y = 0, (c) the kinetic energy of the element, and
(d) the total kinetic energy of the spring. Your answer will
be in the form of 1/2( )ms v2. The
fraction in the ( ) is your answer.
|
|
|
21.
|
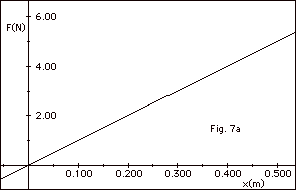
Fig. 7a below is a plot of the extension
of a spring as a function of the force exerted on it. Fig.
7b below is a plot of the square of the period of a mass-spring
system as a function of the mass attached to the spring. The
spring has a mass ms and an effective mass ms’.
(a) Find the spring constant k from Fig. 7a. (b) Write
an expression for the period of a spring with an effective
mass ms’ as a function of the added mass
m. (c) From the intercept on the T2-axis of Fig.
7b, find ms’ and then find ms.
(d) There is another way to find ms’.
Hint: What is m when T2 = 0? Show that this
method gives the same value of ms’ as
that in (b).
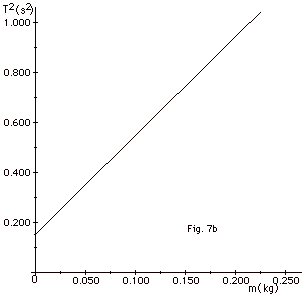
|
|
|
22.
|
A flat plate P moves in simple harmonic
motion with a frequency of 1.5 s-1. A block
rests on the plate (Fig. 8 below). The coefficient of static
friction between the block and the plate is 0.60. Find the
magnitude of the amplitude of the motion if the block does
not slip on the plate.
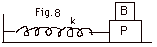
|
|
|
23.
|
Most rigid bodies in the everyday world
are at rest and thus in stable equilibrium. For a body in stable
equilibrium, the net force acting on it is zero. If a body is
displaced a distance x away from the position of stable equilibrium
the force F will be of opposite sign to x. In general
the force is of the form
F = c1 x + c2x2 +
c3x3 + . . . .,
where c1 is a negative constant. The slope
of F vs x at x = 0 is (dF/dx) o = c1.
For small oscillations about the origin, F = ma becomes
c1x = m d2x/dt2
or d2x/dt2 + (-c1/m)x =
0.
Comparing this with the "standard" equation for
simple harmonic motion,
d2x/dt2 + (k/m)x = 0,
we see that the "equivalent" spring constant k is
-c1 = -(dF/dx)o = -[d(-dU/dx)/dx]o
= (d2U/dx2)o.
Suppose the potential energy in a diatomic molecule can be
expressed as the sum of an attractive term b/r3 and
a shorter-range repulsive term a/r5, that is, U =
(a/r5) - (b/r3). Find (a) the equilibrium
position ro, (b) the "spring constant
k" between the two atoms, and (c) the vibrational
frequency of this diatomic molecule if each atom has a mass
m. |
|
|
24.
|
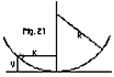
An ice cube is given a small displacement
from the bottom of a spherical bowl of radius R. Given the
equation of the circle in Fig. 21 below is x2 +
(R - y)2 = R2, find (a) the potential
energy U in terms of m, g, x, and R, (b) -dU/dx,
(c) Fx for x << R, and (d) the period
of oscillation when it is released, assuming no friction.
|
|
|
25.
|
Given that the potential energy of a
mass-spring system is 1/2 kx2 show that (a) the
total energy of the system E = 1/2 kA2 = U + K
= 1/2 kx2 + 1/2 mv2 and (b) v = [k/m(A2
- x2)]1/2 = dx/dt. (c) Separate the
variables x and t in (b). Integrate this expression (limits
on t from 0 to t and limits on x from xo to x)
to show that x(t) = A sin [(k/m)1/2t + d].
The initial phase angle d
= sin -1 (xo/A).
|
|
|
26.
|
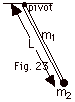
A pendulum consists of a rod of mass
m1 and a point mass m2 (Fig. 23 below).
Find (a) the torque and moment of inertia about the pivot
point, (b) d2Qdt2
in terms of the torque and the moment of inertia and (c) the
period for small oscillations in terms of m1, m2,
L, and g.
|
|
|
27.
|
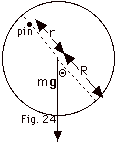
A thin uniform disk with a radius R swings
about an axis that consists of a thin pin driven through the
disk, as shown in Fig. 24 below. Find (a) the moment
of inertia and torque about the axis, (b) d2Q/dt2
in terms of the moment of inertia and the torque, (c) the
period of oscillation and (d) the value of r for a minimum
period of oscillation and the value of the period for this
r.
|
|