|
|
|
1.
|
Show that the work done on an object
equals (a) the product of the displacement and the component
of the force in the direction of the displacement or (b) the
product of the force and the component of the displacement
in the direction of the force.
|
|
|
2.
|
A box rests on a horizontal, frictionless
surface. A girl pushes on the box with a force of 18 N to
the right and a boy pushes on the box with a force of 12 N
to the left. The box moves 4.0 m to the right. Find the work
done by (a) the girl, (b) the boy, and (c) the net force.
|
|
|
3.
|
You support an object and move it to
the right with a constant velocity. You exert a force F
on it (Fig. 1 below) to oppose the gravitational attraction
mg of the earth for the object. If you do not raise
the object or increase its velocity, there is no increase
in the object's potential energy or in its kinetic energy.
Do you do work on the object?

|
|
|
4.
|
An object attached to a string, fixed
at one end, lies on a horizontal, frictionless surface. The
object is given an initial velocity v and moves in a circle
with uniform circular motion. Does the tension in the string
do work on the object?
|
|
|
5.
|
An object of mass m = 2.0 kg is pulled
along a surface by a horizontal force F of 12 N to the right
a distance s of 4.0 m (Fig. 2 below). The coefficient of friction
between the object and the surface is 0.5. Find the work done
by (a) F, (b) the normal force FN,
(c) the weight mg of the object, (d) the frictional
force f, (e) the net force.
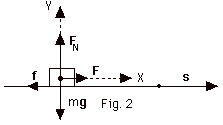
|
|
|
6.
|
A raindrop (m = 3.35 x 10-5
kg) falls vertically at constant speed under the forces of
gravity and air resistance. In falling through 100 m, what
is the work done by (a) gravity and (b) air resistance?
|
|
|
7.
|
A 52-kg skier moves down a slope at a
speed of 14.0 m/s (31.3 mph). Determine the kinetic energy
of the skier.
|
|
|
8.
|
Show that (a) v . v =
v2 and (b) d(v2) = d(v .
v) = 2v . dv = d(v2)
= 2 v dv.
|
|
|
9.
|
The work-energy theorem states that the
work done by the net force on an object of mass m equals
the change in kinetic energy of the object. Derive
the theorem using (a) a non-calculus approach: Assume a constant
Fnet acts through a distance x. Write down an expression
for the result of a net force and then write the constant
acceleration in terms of velocities. (b) a calculus approach:
Integrate 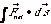 Remember ds = v dt.
Remember ds = v dt.
|
|
|
10.
|
In problem #5, if the initial velocity
of the object vo = 0, find the velocity of the
object after it has been moved a distance of 8.0 m.
|
|
|
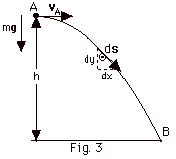
11.
|
A projectile has a velocity vA
parallel to the earth when at a height h (Fig. 3 below). Find
the work done by the gravitational force mg when the
projectile goes from A to B.
|
|
|
12.
|
Use the work-energy theorem to find the
speed of the projectile just as it hits the ground at B in
Fig. 3 above.
|
|
|
13.
|
An object, initially at rest, is pulled
up an incline that makes an angle of 37o with the
horizontal by a force F = 30 N parallel to the incline. The
mass of the object is 2.0 kg and the coefficient of friction
between the object and the surface is 0.5. The object moves
up the incline a distance s = 4.0 m. Find (a) the frictional
force, (b) the work done by F, (c) the work done by the normal
force, (d) the work done by the weight of the object, (e)
the work done by friction, and (f) the velocity of the object
after it has moved 4.0 m.
|
|
|
14.
|
A 2.0-kg object is pushed along a horizontal
surface a distance s = 4.0 m by a force F = 30 N to the right
and down at an angle of 37o to the horizontal.
The coefficient of friction between the object and the surface
is 0.50. Find (a) the frictional force. (b) the work done
by the frictional force (c) the work done by force F, (d)
the work done by the normal force FN, (e) the work
done by the weight of the object, (f) the net work done on
the object and (g) the speed of the object after it moves
through s = 4.0 m if its initial speed = 0.
|
|
|
15.
|
A constant force of 10 N is exerted to
lift a l.0-kg mass a vertical height of 1.0 m. Find (a) the
work done by the person, (b) the work done by the gravitational
force, (c) the increase in its gravitational energy, and (d)
the increase in its kinetic energy. Take g = 10 m/s2.
|
|
|
16.
|
Repeat Problem #15 for a constant force
of 12 N.
|
|
|
17.
|
A box of mass 12 kg slides at a speed
of 10 m/s across a smooth level floor, where it enters a rough
portion 3.0 m in length. In the rough portion, the box experiences
a horizontal frictional force of 72 N. (a) How much work is
done by the frictional force? (b) What is the velocity of
the box when it leaves the rough surface? (c) What length
of rough surface brings the box completely to rest? Take g
= 10 m/s2.
|
|
|
18.
|
(a) How much work is required to push
a 2.0-kg object up a frictionless inclined plane whose length
is 2.0 m and whose height is 1.0 m, if the velocity of the
object remains constant? (b) How much work is required to
push the object up the plane while increasing its velocity
from zero to 3.0 m/s? (c) How much work is required to push
the object up the plane at a constant speed if there is a
frictional force of 3.0 N between the object and the plane?
Take g = 10 m/s2.
|
|
|
19.
|
A block of mass 1.0 kg is placed at
the top of an incline of length 125 m and height 62.5 m. The
plane has a rough surface. When the block arrives at the bottom
of the plane it has a velocity of 25 m/s. What is the magnitude
of the constant frictional force acting on the block? Take
g = 10m/s2.
|
|
|
20.
|
Assume that the total energy of an electron
bound to a proton in the hydrogen atom is -21.7 x 10-19
J. What is the kinetic energy of the electron (we assume
the proton is at rest) when the potential energy of the atom
is -43.4 x 10-19 J?
|
|
|
21.
|
A 2000-kg car is at rest on a level frictionless
track. A constant force acts on it for one-half second, after
which the car is moving with a speed of 0.20 m/s. Find (a)
the magnitude of the force, (b) the kinetic energy of the
car, (c) the work done on the car, and (d) the displacement
of the car.
|
|
|
22.
|
Find 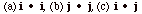 (d)
the work done if the force F = 20 N j and the
displacement s = 4 m i and (e) the work done
if the force F = (3i + 4j)N and the displacement
s = (2i - 2j) m. (d)
the work done if the force F = 20 N j and the
displacement s = 4 m i and (e) the work done
if the force F = (3i + 4j)N and the displacement
s = (2i - 2j) m.
|
|
|
23.
|
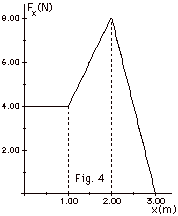
An object is subjected to a force along
the X-axis as shown in Fig. 4 below. Find the work done on
the object as it moves from (a) x = 0 to x = 1 m, (b) x =
1 m to x = 2 m and (c) x = 2 m to x = 3 m. If the mass of
the object m = 2.0 kg and its initial velocity vo
= 0, use the work-energy theorem to find (d) v1
the velocity at x = 1.0 m, (e) v2 the velocity
at x = 2.0 m and (f) v3 the velocity at x = 3.0
m.
|
|
|
24.
|
The only force acting on an object is
F = (4.0 N + 6.0 N/m x)i. The object, initially
at rest, is moved through s = 2.0 mi. Find (a)
the work done on the object and (b) its velocity after it
has moved 2.0 m.
|
|
|
25.
|
A spring obeying Hooke's law has k =
50 N/m. When suspended vertically its equilibrium length is
0.50 m. Determine the new equilibrium length when a 0.50 kg
object is attached to it. Take g = 10 m/s2.
|
|
|
26.
|
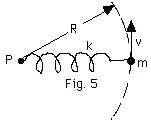
A ball of mass m = 1.0 kg is attached
to a spring and the spring is attached to a fixed point P,
as shown in Fig. 5 below. The spring cannot bend. The ball
is moving in a circle of radius R in a horizontal plane with
a velocity v. The spring is massless and the plane on which
the ball moves is frictionless. (a) If R = 1.0 m and v = 1.0
m/s, what is the tension in the spring at the point where
it attaches to m? (b) If the relaxed length of the spring
is 0.90 m, what is the spring constant k? (c) If the ball
and spring now rotate with v = 2.0 m/s, what is the new radius
of the ball's path. (d) How much work is done on the mass
and on the spring.
|
|
|
27.
|
The potential energy difference Uf
- Ui between two points i and f is defined as the
negative integral from i to f of Fc .
ds, where Fc is a conservative
force:
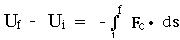
Find (a) the potential energy difference and (b) the potential
energy for
Fc = -kx2 i.
|
|
|
28.
|
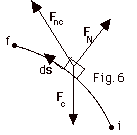
In Fig. 6 below, an object is acted upon
by three forces: FN a normal force,
Fc a conservative force such as a gravitational
force or a force due to a spring, and Fnc a
nonconservative force such as a push or a pull or a frictional
force. The net force acting on the object is:
Fnet = N + Fc
+ Fnc, or
Fnc = Fnet - N
- Fc
If we take the dot product of each force with ds and
then integrate,
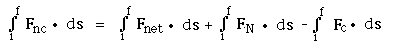
(a) Identify each term on the right side of the above equation
and find
what they equal.
(b) Show that the work done by the nonconservative force =
(Uf +Kf) - (Ui + Ki).
(c) What happens when Fnc = 0.
|
|
|
29.
|
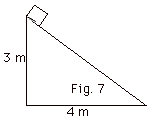
An object of mass m = 2.0 kg is released
from rest at the top of the frictionless incline of Fig. 7
below. Taking g = 10 m/s2, use energy considerations
to find the velocity of the object at the bottom of the incline.
|
|
|
30.
|
Repeat #29 when µk between
the object and the plane is 1/4.
|
|
|
31.
|
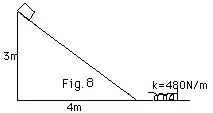
When the block in #29 reaches the bottom
of the incline it compresses a light spring (Fig. 8 below).
If the spring constant k = 480 N/m, what is the maximum compression
of the spring?
|
|
|
32.
|
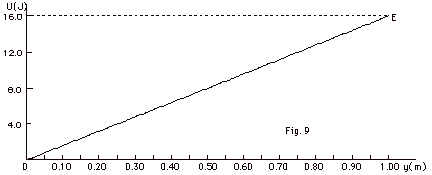
Figure 9 below is a plot of the potential
energy U of a freely falling object as a function of the height
y above the ground. E = 16.0 J (shown by the dashed horizontal
line) is the total mechanical energy of the object. Find (a)
the potential energy and (b) the kinetic energy of the object
for y = 0.75 m. Find (c) the mass of the object and (d) v
when y = 0.75 m. Take g = 10 m/s2.
|
|
|
33.
|
Figure 10 below is a plot of the potential
energy of a mass-spring system. The total mechanical energy
E of the system = 0.200 J. Find (a) the potential energy U
and (b) the kinetic energy K at x = 0.025 m. Find (c) the
spring constant k and (d) the speed of the particle when x
= 0.025 given that the mass of the object m = 0.30 kg. Find
(e) the amplitude of the motion and (f) the maximum velocity
of the object.
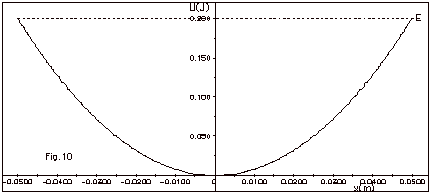
|
|
|
34.
|
A block with mass m = 1.0 kg slides
to the right on a horizontal surface. The coefficient of kinetic
friction between the surface and the block is 0.3. The block
approaches a massless spring with spring constant k = 10 N/m.
The dashed vertical line in Fig. 11 below is the unstretched
position of the spring. (a) When the block makes contact with
the spring at its unstretched position, its velocity is via
= 4.0 m/s. It then compresses the spring a distance x and
comes to rest. Find x. (b) The block then moves to the left.
Find the velocity vfb when the spring is in its
unstretched position. (c) Find the distance dc
from the unstretched position when the block comes to rest.
Take g = 10 m/s2.
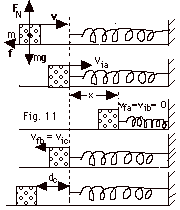
|
|
|
35.
|
A block of mass m = 2 kg is held at the
top of an incline plane that makes an angle of 37o
with the horizontal. The initial position of the block is
shown in Fig. 12 (i) below where it is a distance s =
1.0 m from a spring with constant k = 120 N/m. In Fig. 12 (f)
below, I show the final position of the block. (a) Look at
Fig. 12 (i) and Fig. 12 (f) and decide where to
take the zero of gravitational potential energy. (b) Having
made your decision in (a) what is the potential energy of
the system for the initial position? (c) What is the kinetic
energy of the system for the initial position? The coefficient
of kinetic friction between the surface and the block is 1/8.
(d) What is the frictional force that acts on the block as
it goes down the incline? As the block makes contact with
the spring, it continues to move until it compresses the spring
to a maximum distance x. For the "final position",
find (e) the final potential energy, (f) the final kinetic
energy, (g) the work done by the frictional force. (h) Put
this all together and find x. Take g = 10 m/s2.
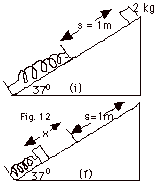
|
|
|
36.
|
A small block of mass m slides along
the frictionless loop-the-loop shown in Fig. 13 below. Find
(a) the minimum height h above the bottom of the track which
you must release the block so that it will not leave the track
at the top of the hoop and (b) the force of the track on the
sphere at P in Fig. 13 when it is released from the height
h found in (a). Take g = 10 m/s2.
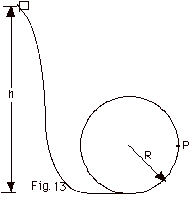
|
|
|
37.
|
A bob of mass m is suspended from a string
of length L. The bob is pulled to the left so the string makes
an angle Q with the vertical
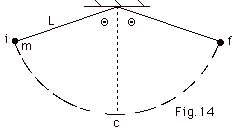
(Fig. 14 below). The bob is released and vibrates back and
forth from position i to c to f, back to c and then back to
i, where the motion starts over again. Find the tension in
the string at positions i, c, and f.
|
|
|
38.
|
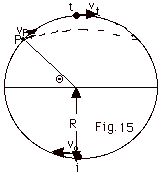
A point mass m starts with speed vo
at i and moves in a vertical circle along the frictionless
surface of radius R (Fig. 15 below). (a) What is the minimum
value of vo such that the mass makes it around
the circle. (b) Now take v = 4/5 of the value found in (a).The
particle moves up to some point P shown in the figure, loses
contact with the track, and travels approximately along the
dashed track shown in Fig. 15. Find the position of P.
Take g = 10 m/s2.
|
|
|
39.
|
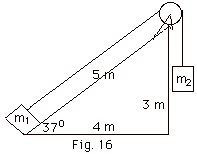
In Fig. 16 below, the first block has
a mass m1 = 2.0 kg and the second block has m2
= 4.0 kg. The pulley and string are massless. There is no
friction in the pulley, but the coefficient of kinetic friction
between the first block and the incline is µk
= 0.55. The blocks are released from rest. Use energy
considerations to find the speed of the two blocks when the
second block has moved down 2.5 m. Take g = 10 m/s2.
|
|
|
40.
|
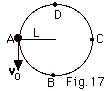
A very light rod of length L has a ball
of mass m attached to one end. The other end rotates about
a pivot without friction. The system rotates in a vertical
circle starting at position A in Fig. 17 below with downward
velocity vo. When the ball reaches D, it
stops and swings back down in a clockwise direction. Find
(a) an expression for vo in terms of L, m, and
g and (b) the tension in the rod at position B. A little sand
gets into the pivot and then the ball only reaches C when
launched from A. Find (c) the work done by friction during
the motion from A to C and (d) how much total work is done
by friction when the ball finally comes to rest at B after
oscillating back and forth a few times.
|
|
|
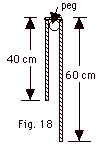
41.
|
A rope with a mass of 0.20 kg and length
of 1.0 m hangs, initially at rest, on a frictionless peg that
has a negligible radius (Fig. 18 below). Use conservation
of energy to find the vertical velocity of the rope just as
the end slides off the peg. Take g = 10 m/s2.
|
|
|
42.
|
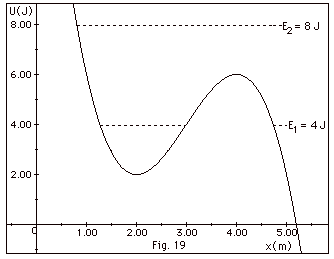
A particle with a mass m = 2.0 kg has
a potential energy function
U(x) = 3 J/m x - 5 J - (x m-1 - 3 )3
J
For a particle initially at (a) x = 2.0 m and (b) x = 5.0
m describe its motion for
2.0 J < E < 6.0 J. (c) Describe the motion for a particle
initially at x = 2.0 m and moving to smaller values of x for
E > 8.0 J. (d) Find the speed of the particle at x = 3.0
m and E = 8.0 J. Find the force on the particle at (e) x =
1.26 m and (f) 3.00 m by finding the negative of (i) the slopes
at these two points and (ii) the derivative of U at these
two points.
|
|
|
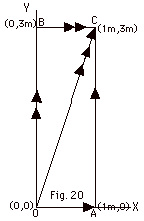
43.
|
Given F = 2.0 N/m3
xy2 i + 2.0 N/m3 yx2
j. Find the work done by this force in going from (a)
O to A to C, (b) O to B to C, (c) O to C and (d) 0 to A to
C to 0 (Fig. 20 below). (e) Is the force conservative?
|
|