|
Answers - Simple Harmonic Motion
|
|
|
1.
|
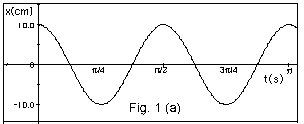
- The maximum displacement from the equilibrium position
A = 10.0 cm.
- The time for one complete oscillation T = p/2
s. Notice the maximum positive displacement x
= +10.0 cm occurs at t = 0 and the next time
at t = p/2 s.
It occurs again at t = ps.
|
|
|
2.
|
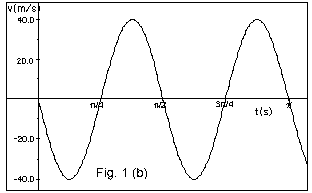
- v(t) = - (2p/T)(A
sin 2pt/T). The
maximum value of the sine is 1. The maximum absolute
value of v = 2pA/T.
The ± signs account only for the direction
of the velocity.
- From Fig. 1b above, |vmax|
= 40.0 cm/s = 2pA/T =
2p(10cm)/ps/2.
|
|
|
3.
|
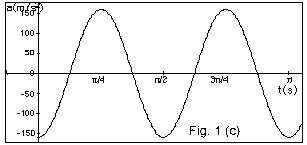
- a(t) =- (2p/T)2(A
cos 2pt/T).
Maximum value of the cosine is
1. |amax| = (2p/T)2A.
The ± signs account only for the direction
of the acceleration.
- a(t) = - (2p/T)2
(A cos 2pt/T) =
- (2p/T)2
x(t)
since x(t) = A cos 2pt/T.
-a(t)/x(t) = (2p/T)2.
- From Fig. 1c above,
|amax| = 160.0 cm/s2
= (2p/T)2A
= (2p/ps/2)2
10 cm.
|
|
|
4.
|
- For a mass attached to a spring, F = - kx
or F/x = - k, where k is a constant.
The applied force F is directly proportional to the
displacement x and the minus sign says it is in the
opposite direction to x.
- When the spring is extended and released, Fnet
= ma or
- kx = ma or
- a/x = k/m.
- From 3a(ii), - a(t)/x(t) = (2p/T)2
By comparison, k/m = (2p/T)2
or
T = 2p(m/k)1/2.
|
|
|
5.
|
- Given x(t) = A cos (2pt/T
+ d), where A is the
maximum displacement from the equilibrium position. The
maximum value of cos (2pt/T
+ d) is 1, so the equation
accurately describe the definition of A.
- x(t + T) = A cos [2p(t
+ T)/T + d]
=
A cos [2pt/T + 2pT/T+
d]
=
A cos [2pt/T + 2p
+ d]
=
A cos (2pt/T + d)
= x(t).
The definition of T is accurately described by the equation
of motion for simple harmonic motion, A cos (2pt/T
+ d), because
it allows the value of x at t to equal
the value of x at t + T or
t + nT where n = 1, 2, 3 . . .
- For x(t) = A cos (2pt/T
-p /2), x(0) =
xo = A cos (- p
/2) = 0.
v(t) = - (2p/T)A
sin (2pt/T-
p /2).
v(0) = vo = - (2p/T)A
sin (- p /2) = (2p/T)A
= +vmax.
At t = 0, the object is at the equilibrium position
and travelling with the maximum velocity in the +X-direction.
|
|
|
6.
|
Given that d2x/dt2
+ (k/m)x = 0
(Equation
1")
Show that x(t) = A cos (2p t/T
+ d) is a solution.
(Equation
1')
v = dx/dt = - (2p/T)A
sin (2pt/T + d).
dv/dt = d2x/dt2 = - (2p/T)2[A
cos (2p\t/T + d)]
= - (2p/T)2 x
(Equation
2)
Substituting Eq. 2 into Eq. 1", - (2p/T)2
x + (k/m)x = 0.
This equation is true if (2p/T)2
= (k/m) or
T = 2p(m/k)1/2.
|
|
|
7.
|
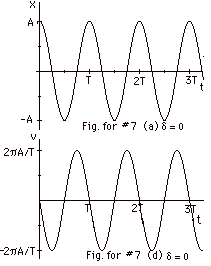
In general, x(t) = A cos (2pt/T
+ d) and
v(t) = dx/dt = -A(2p/T)
sin (2pt/T + d).
(a) and (d)
In Fig. for #7a above, x(t) is plotted for
d = 0.
In Fig. for #7d above, v(t) is plotted for
d = 0.
For d
= 0 and t = 0 , the initial conditions are:
the initial displacement = xo = A and
the initial velocity = vo = 0.
Immediately after t = 0, the object moves to the
left (with a negative velocity).
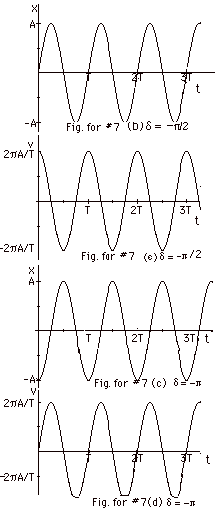
(b) For d = - p/2,
x(t) = A cos (2pt/T - p/2).
By trigonometric identity,
cos (C - D) = cos C cos D + sin C sin D (with C
= 2pt/T and D = p/2)
x(t) = A[cos 2pt/T cos
p/2 + sin 2pt/T
sin p/2]
x(t) = A[cos 2pt/T(0)
+ sin 2pt/T(1)] = A sin
2pt/T
Notice the first maximum in Fig. b (immediately
above) lags that in
Fig. a (above) by p/2
radians.
(e) v(t) = - 2pA/T
sin (2pt/T - p/2)
By trigonometric identity,
sin (C - D) = sin C cos D - cos C sin D
v(t) = -2pA/T[(sin 2pt/T)(0)
- (cos2pt/T)(1)]
v(t) = (2pA/T) cos 2pt/T
For d
= - p/2 and
t = 0, xo = 0 and
vo = +2pA/T
(c) For d = - p,
x(t) = A cos (2pt/T
- p)
=
A[cos 2pt/T cos p
+ sin 2pt/T
sin p]
=
A[(cos 2pt/T)(-1) + (sin
2pt/T)(0)]
x(t) = - A cos 2pt/T
Notice that Fig. c (immediately above)
lags Fig. a (above) by p
radians.
(f) v(t) = - A(2p/T)
sin (2pt/T - p)
=
- (2pA/T)[sin 2pt/T
cos p-cos 2pt/T
sin p]
=(- 2pA/T)[(sin2pt/T)(-1)
- (cos2pt/T)(0)].
v(t) = (2pA/T)
sin 2pt/T
For d
= - p and
t = 0, xo = - A and
vo = 0.
Immediately after t = 0, the object moves to the
right with a positive velocity.
(g) The function of d is
to state the initial conditions.
Note: d
= p or
- p gives
the same result.
|
|
|
8.
|
- x(t) = A cos (wt +
d)
x(0) = xo = A cos d
(Equation
1)
- v(t) = dx/dt = - wA
sin (wt + d)
v(0) = vo = -wA
sin d
(Equation
2)
Dividing both sides of Eq. 2 by - w:
- vo/w =
A sin d
(Equation
3)
- Dividing Eq. 3 by Eq. 1, tan d =
- vo/xwo.
- Squaring Eq. 1 and Eq. 3 and adding:
xo2 + (- vo/w)2
= A2(cos2 d
+ A sin2 d)
or
[xo2 + (- vo/w)2]1/2
= A.
|
|
|
9.
|
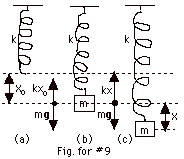
In Fig. for #9(a) above, the spring is not stretched. In Fig.
for #9(b) above, the mass is attached and the spring is stretched
a distance xo.
- The mass comes to rest and Fnet = ma = m(0).
Taking down to be positive,
- kxo + mg = 0 (Equation
1)
- In Fig. for #9(c) above, the spring has been displaced
an additional distance x. Now Fnet = ma, where a ≠
0 once the spring is released. Taking the direction of x,
which is down, as positive,
- kx - kxo + mg = ma (Equation
2)
From Eq. 1, we see that - kxo + mg = 0. Eq.
2 becomes:
- kx = ma or
- a/x = k/m.
The ratio of a to x is the same
whether the spring is mounted horizontally or vertically.
- As before, - a/x = (2p/T)2
= (2pf)2
= k/m and
f = (1/2p)(k/m)1/2.
|
|
|
10.
|
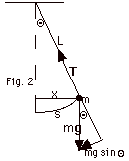
- The forces acting on the pendulum bob are its weight mg
and the tension T in the string.
- The only force tangent to the path is a restoring force
- mg sin Q. From
the triangle with lengths, we find that
sin Q =
x/L and - mg sin Q
= - (mg/L)x.
For small displacements, x ≈ s, we can think of the
displacement and the restoring force acting horizontally.
Fnet
= ma
- (mg/L)x = ma
- Since m, g, and L are constants, the restoring force,
- (mg/L)x, is directly proportional to the displacement
and in the opposite direction. The pendulum is an example
of simple harmonic motion.
-a/x = (g/L) = (2p/T)2
= (2pf)2.
f = (1/2p)(g/L)1/2.
For another approach, write Q
= s/L. For small angles Q
is approximately equal to sin Q.
The restoring force - mg sin Q
≈ - mgQ =
m d2s/dt2
= m d2(LQ)/dt2,
or - (g/L)Q = d2Q/dt2
and d2Q/dt2
+ (g/L)Q = 0.
This is the same form as d2x/dt2 +
(k/m)x = 0, for which T = 2p
(m/k)1/2 and x = A cos (2p/T).
By comparison with the spring, for the pendulum T = 2p
(L/g)1/2 and f = 1/T = (1/2p)(g/L)1/2
and Q = Qmax
cos (2p/T).
|
|
|
11.
|
Given x(t) = 0.01 m cos (0.02p
s-1 t - p/2)
compare with x(t) = A cos (2p t/T
+ d) and find:
- the amplitude A = 0.01 m
- 2p/T = 0.02p
s-1; period T = 100 s,
- the frequency f = 1/T = 0.01 s-1,
and
- the initial phase d
= - p/2.
|
|
|
12.
|
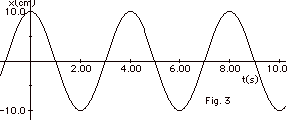
From Fig. 3 above, we see that:
- The cosine curve repeats itself every 4.0s so the period
T = 4.0 s.
- The amplitude of the motion A =10.0 cm.
- If we write the equation of motion as a function of the
cosine, we let d = 0.
x(t) = A cos 2pt/T =
10.0 cm cos 2pt/4.0
s = 10.0 cm cos pt s-1/2.
- v(t) = dx/dt = -10.0p/2
cm/s sin pt s-1/2
|vmax| = 5.0p
cm/s
- a(t) = dv/dt = -10.0 (p/2)2cm/s2
cos pt s-1/2
|amax| = 2.5p2
cm/s2
|
|
|
13.
|
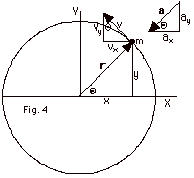
For the X-component:
(a) x = r cos Q = r
cos wt
(b) vx = dx/dt = - wr
sin wt
ax = dvx/dt
= - w2 (r
cos wt) = - w2x
(c) ax/x = - w2
= - 4p2f2
(d) (e) Since the acceleration is directly proportional to the
displacement and in the opposite direction, the motion is simple
harmonic. Remember by Newton's second law of motion the acceleration
is directly proportional to, and in the same direction as, the
force.
(f) ax/x = - w2
= - 4p2f2
= - k/m or
w = 2pf =
(k/m)1/2
For the Y-component:
(a) y = r sin Q = r sin
wt
(b) vy = dy/dt = wr
cos wt
ay = dvy/dt
= - w2(r
sin wt) = - w2y
(c) ay/y = - w2
= - 4p2f2
(d) (e) The motion is again simple harmonic, and
(f) ay/y = - w2
= - 4p2f2
= - k/m or
w = 2pf
= (k/m)1/2
|
|
|
14.
|
For a mass-spring system,
- kx = ma = md2x/dt2 or
d2x/dt2 + (k/m)x = 0, where the period
T = 2p (m/k)1/2.
By comparison with
b2d2x/dt2 + c2x
= 0 or
d2x/dt2 + (c/b)2x = 0,
we see that in this case T = 2p
(b/c).
|
|
|
15.
|
For a total swing back and forth of 4.0
cm, the amplitude A is 2.0 cm.
For x(t) = A cos 2pt/T,
v(t) = dx/dt = - A2p/T
sin 2pt/T.
The maximum velocity of the pendulum occurs at the center of
the swing equal to 10 cm/s.
|vmax| = 2pA/T.
T = 2pA/vmax=
2p (2.0 cm)/10 cm/s = 0.4p
s.
|
|
|
16.
|
x(t) = 4.0 cm cos (pt
s-1 - p/6).
2.0 cm = 4.0 cm cos (pt
s-1 - p/6).
cos (pt s-1 -
p/6) = 0.5 and
(pt s-1 - p/6)
= p/3 (60o).
v(t) = dx/dt = - 4.0p
cm/s sin (pt s-1
- p/6).
When (pt s-1 -
p/6) = p/3,
sin p/3 = 0.866
and
v = - 4.0p (0.866)
cm/s
= - 10.9 cm/s.
|
|
|
17.
|
w= 2pf = 2p
(3/2 s-1) = 3p
s-1. xo = 0.25 m and
vo = - 1.5 m/s.
We know that 0 < d
< p/2 because xo
is positive and vo is negative. The initial position
of the object is less than the amplitude, but positive, and
moving toward the equilibrium position with a negative velocity.
As shown in #8 above,
A = [(xo)2 + (- vo/w)2]1/2
= [(0.25 m)2 + (1.5 m/s/3p
s-1)2]1/2 = 0.296 m.
tan d = - vo/wxo
= 1.5 m/s/(0.25 m)(3p s-1)
= 0.637.
tan-1 0.637 = 0.18p
= 32.5o.
x(t) = A cos (2pt/T + d)
= 0.296 m cos (3pt s-1
+ 0.18p).
Plots of position x and the velocity v as a function of t
are shown in 17a and 17b above, respectively. Note xo
= 0.25 m and vo = - 1.5 m/s.
|
|
|
18.
|
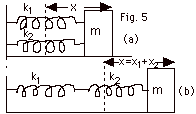
Fnet = ma = m d2x/dt2
For Fig. 5a,
- k1x - k2x = - (k1
+ k2)x = m d2x/dt2 or
d2x/dt2 + [(k1 + k2)/m]x
= 0.
Compare with
d2x/dt2 + [k/m]x = 0 when
f = (1/2p)(k/m)1/2
and find for this case,
f = (1/2p)[(k1
+ k2)/m]1/2.
The "effective" spring constant for springs in parallel
is keff = k1 + k2 . . + kn.
For Fig. 5b, the spring with constant k2 is in contact
with mass m that has a displacement x = x1
+ x2, where x1 is the extension
of the spring with constant k1 and x2
is the extension of the spring with constant k2.
The force on the object is:
- k2x2 and
- k2x2 = m d2x/dt2 (Equation
1)
Also,
x = x1 + x2
(Equation
2)
and the magnitude of the force on the second spring due to the
first spring equals the magnitude of force on the first spring
due to the second spring, or
k1x1 = k2x2
or
x1 = k2x2/k1
(Equation
3)
Substituting Eq. 3 into Eq. 2,
x = (k2x2/k1) +
x2 = (k1 + k2)x2/k1
, or
x2 = k1x/(k1 + k2)
(Equation
4)
Substituting Eq. 4 into Eq. 1,
- [k2k1/(k1
+ k2)]x = m d2x/dt2
or
d2x/dt2 + [{k1k2/(k1
+ k2}/m)]x = 0.
Comparing with
d2x/dt2 + [k/m]x = 0
For this case,
f = (1/2p)[{k1k2/(k1
+ k2)}/m]1/2.
The "effective" spring constant for series is:
keff = {k1k2/(k1
+ k2} or
1/keff = 1/k1 + 1/k2 + .
.+ 1/kn.
|
|
|
19.
|
Imagine the spring cut into thirds with
each part having a spring constant k’. When the three
springs are connected in series, the spring constant is
k = 10.0 N/m.
For series,
1/k = 1/10 N/m = 1/k’ + 1/k’ + 1/k’=
3/k’
k’ = 3k = 30.0 N/m.
When two of these springs with k’ are connected in series,
1/k” = 1/k’ + 1/k’ = 2/30 N/m,
or the spring constant with 2/3 of the spring left (1/3 cut
off) is
k” = 15 N/m.
T= 2p(m/k”)12
= 2p(0.30/15)1/2 s
= 2p (0.02)1/2
s.
|
|
|
20.
|
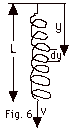
- The differential mass dm = msdy/L
(Fig. 6 above)
- Assuming the velocity vy at y increases
linearly with y from 0 at y = 0
to v at y = L, vy = vy/L.
- dK = 1/2 dm vy2 = 1/2(msdy/L)(vy/L)2.
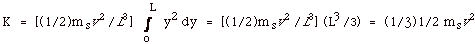
The effective mass that takes place in the oscillation is
ms/3.
The fraction of the mass is 1/3.
|
|
|
21.
|
- The slope of force F as a function of the extension x
is
k = (5.0 - 0)N/(0.50 - 0)m = 10 N/m.
- For a total mass M and force constant k, the period of
the motion is
T = 2p(M/k)1/2.
For a spring of effective mass ms’, M
= m + ms’, where m is the variable
mass added to the spring load. For this case
T = 2p (m
+ ms’)/k]1/2 or
T2 = (4p2/k)m
+(4p2/k)ms’
(Equation
1)
If we compare Eq. 1 to the equation of a line, y = (slope)x
+ (y-intercept), we see that T2 versus
m should yield a straight line and the intercept on the
T2 axis is (4p2/k)ms’.
From Fig. 7a above, we find k = 10 N/m. From Fig.
7b above, we find the intercept on the T2 axis
= 0.154 s2 = (4p2/k)ms’
= (4p2/10
N/m)ms’. ms’ = (1.54/4p2)kg
= 0.390 kg and ms = 3 x (0.390 kg) = 0.117 kg
= 117 g.
- When T2 = 0 in Eq. 1, 0 = (4p2/k)m
+ (4p2/k)ms’
or
ms’ = - m = - (-0.0390
kg).
ms’ = 0.0390 kg, agreeing with the value
found in part (b).
- P.S. It helps to have my graphing program that reads
off coordinates.
|
|
|
22.
|
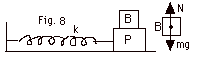
For simple harmonic motion, a/x = - w2.
For maximum acceleration, |amax|
= Aw2.
For motion in the vertical direction, (Fnet)y
= may = m(0) or
N - mg = 0 and N = mg.
The frictional force that keeps the block from slipping on the
plate f = µN = µmg = ma = mAw2.
A = µg/w2
= 0.60(10 m/s2)/(1.5 s-1)2 =
2.7 m.
|
|
|
23.
|
- For the equilibrium position, dU/dr = 0 = (-5a/r6)
+ (3b/r4).
Calling r = ro at the equilibrium position,
ro = (5a/3b)1/2.
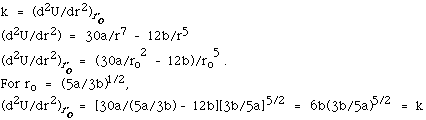
The reduced mass µ = m/2 and the frequency f = (1/2p)(k/µ)1/2
=
(1/2p)[(12b/m)(3b/5a)5/2]1/2.
|
|
|
24.
|
- U = mgy
- dU/dx = d(mgy)/dx = mg.
d[R - (R2 - x2)1/2]/dx
= mgx/(R2 - x2)1/2.
For x < < R, dU/dx = mgx/R. Fx
= - dU/dx = - (mg/R)x.
The force Fx is directly proportional to the
displacement x and in the opposite direction. The motion
is simple harmonic.
- Fx
= ma or
- (mg/R)x = m d2x/dt2 and
d2x/dt2 + (g/R)x = 0.
Compare d2x/dt2
+ (k/m)x = 0 (for which T = 2p(m/k)1/2)
and see for this case T= 2p(R/g)1/2.
|
|
|
25.
|
- When x = A, v = 0 and K = 0. In general, E
= U + K = 1/2 kx2 + 1/2 mv2. When
x = A, E = 1/2 kA2 + 1/2 m(0) = 1/2 kA2.
Since E is a constant, E always equals:
1/2 kA2 = 1/2 kx2 + 1/2
mv2
(Equation
1)
- Multiplying Eq. 1 by 2/m gives:
(k/m)A2 = (k/m)x2 +
1/2 mv2 or
(k/m)(A2 - x2) = v2 and
v = dx/dt = (k/m)1/2(A2
- x2)1/2.
- Separating variables dx/(A2 - x2)1/2 =
(k/m)1/2 dt.
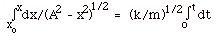
Let x = A sin Q, dx
= A cos Q dQ.
(A2 - x2)1/2 = A(1 - sin2
Q)1/2 = A
cos Q.
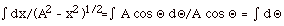
For limits on Q, xo
= A sin Qo
and sin Qo
= xo/A.
The lower limit is sin -1 xo/A and
the upper is sin -1 x/A.
Integrating the above equation gives:
sin -1 x/A + sin -1 xo/A
= (k/m)1/2t or
sin -1 x/A = (k/m)1/2t + sin -1
xo/A.
Letting sin -1 xo/A = d,
sin -1 x/A = (k/m)1/2t
+ d or
x(t) = A sin [(k/m)1/2t + d].
|
|
|
26.
|
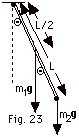
- t = r x
F. t=
rF sin
 r,
F. About the pivot point, the torque for the
rod of mass m1 is -(L/2)m1g sin Q
and for the point mass it is -Lm2g sin Q.
The negative signs occur because they are restoring torques.
When the pendulum is swinging counterclockwise, the torque
tends to make it swing clockwise. The moment of inertia
of the rod about an end is 1/3 m1L2.
The moment of inertia of a point particle of mass
m2 a distance L from the axis is m2L2.
- t = Ia
-Lg(m1/2 + m2)sin Q=
(m1/3 + m2)L2 d2Q/dt2
For small Q, sin
Q is approximately
equal to Q and
d2Q/dt2
+ [g(m1/2 + m2)/(m1/3
+ m2)L]Q
= 0.
Comparing with
d2x/dt2 + [k/m]x = 0 (for
which Period = 2p
(m/k)1/2),
we find for this pendulum,
Period = 2p
[2(m1 + 3m2)L/(m1 + 2m2)3g]1/2
|
|
|
27.
|
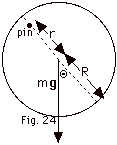
For oscillations about pin axis (Fig. 24 above),
- t =
r x F.
t = rF sin r,F
= -rmg sin Q ≈
-rmg Q for small
Q.
The moment of inertia about the pin a distance r from the
center of mass,
I = (1/2 mR2 + mr2).
- t= Ia
= (I)d2Q/dt2
-rmgQ = (1/2 mR2
+ mr2)d2Q/dt2
- or
d2Q/dt2
+ [rg/(1/2 R2 + r2)]Q
= 0.
Compare with
d2x/dt + [k/m]x = 0 (for which Period
= 2p[m/k]1/2)
and see for the disk,
Period = 2p[(R2
+ 2r2)/2rg]1/2.
- For a minimum period,
d(Period)/dr = 0 =
2p(1/2)[(2rg)(4r) -
(R2 + 2r2)2g]/4r2g2][(R2
+ 2r2)/2rg]1/2 or
(2rg)(4r) = (R2 + 2r2)2g or
4r2 = R2 + 2r2 and
2r2 = R2 or
r = R/(2)1/2.
|
|
