Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 108

Answers - Physical Optics

1.



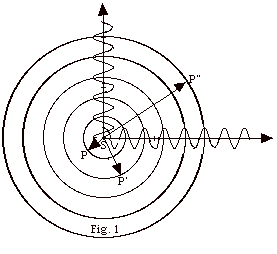
  1. The concentric circles are cross-sections of spherical wave fronts that pass through the crests of the waves. The distance between crests equals one wavelength l.

  2. The distance SP is from one crest to another or l.

  3. The distance SP’ is 2l.

  4. The distance SP” is 5l.

  5. The distance between a crest and a trough is l/2. The wavefronts through troughs would be spheres halfway between the spheres that represent the wavefronts through the crests. In the figure you would represent their cross-sections with circles.

2.




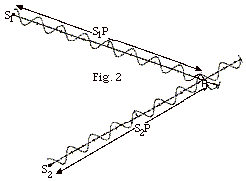
  1. Counting the number of crests from S1 to P you find S1P = 8l.

  2. Counting the number of crests from S2P = 7l.

  3. The path difference S1P - S2P = l.

  4. For a path difference of an integral number of wavelengths, there will be constructive interference.

3.

 Frequency f is the number of oscillations of the source of the wave per second, wavelength l is the distance traveled by the wave in one complete oscillation of the source and velocity is the distance traveled by the wave in one second.

number of oscillations x distance traveled = distance traveled
second oscillation second
f x l = v

4.

For the first minimum, the path difference = l/2 = (10 - 8)ft = 2 ft and the wavelength l= 4 ft. The speed of sound v = lf = (4 ft)(275 s-1) = 11 x 102 ft/s.

5.


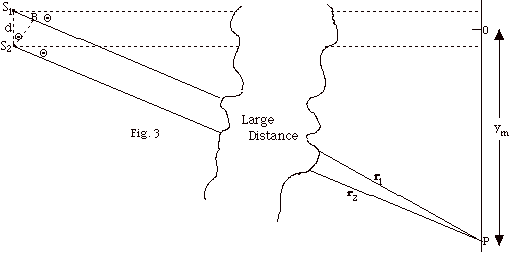
  1. For a maximum the path difference equals an integral number of wavelengths, l, 2l, 3l, . . .  S1P = ml, where m = 0, 1, 2, 3, . . . .

  2. In triangle BS1S2 of Fig. 3 above, sin Q = S1B/d = ml/d,
    or ml = d sin Q for a maximum.

  3. For a minimum the path difference equals l/2, 3l/2, 5l/2, . . .
    S1P = (m + 1/2)l, where m = 0, 1, 2, 3, . . . .

    In triangle BS1S2,  sin Q = S1B/a = (m + 1/2)l/d,
    or m(1 + 1/2)l = d sin Q for a minimum.

6.



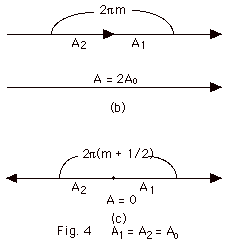
For Fig. 4b above,
  1. The resultant amplitude A = A1 + A2 = 2Ao,  where A1 = A2 = Ao.
  2. The phase difference = 0, 2p, 3p, . . . or  DF = 2mp,
    m = 0, 1, 2, 3, . . .
For Fig. 4c above,
  1. The resultant amplitude A = A1 - A2 = 0,  where A1 = A2 = Ao.
  2. The phase difference = p, 3p, 5p, . . . or  DF = 2p(m + 1/2),
    m = 0, 1, 2, 3, . . .

7.

   DF = 2p(r1 - r2)/l = 2p (path difference)/l.
  1. For constructive interference, DF= 2pm = 2p (r1 - r2)/l
    or path difference = (r1 - r2) = ml,  m = 0, 1, 2, 3, . . .

  2. For destructive interference, DF= 2p (1 + 1/2)m = 2p (r1 - r2)/l
    or path difference = (r1 - r2) = m(1 + 1/2)l,  m = 0, 1, 2, 3, . . .

8.



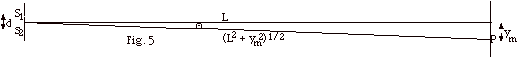
In Fig. 5 above, sin Q= ym/(L2 + ym2)1/2 ≈ ym/L = tan Q for small Q.
  1. For constructive interference sin Q = ml/d ≈ ym/L.
    Dropping the approximate sign,  ym = mlL/d.

  2. Dy = ym+1 - ym = (m + 1)lL/d - mlL/a = lL/d.

  3. For destructive interference sin Q = (m + 1/2)l/d ≈ ym/L.

    1. ym = (m + 1/2)lL/d.

    2. (b) Dy = ym+1 - ym = (m + 1 + 1/2)lL/d - (m + 1/2)lL/d = lL/d.

9.

  From Fig. 4a below, Ax = A2 + A1 cos DF.   Ay = A1 sin DF.

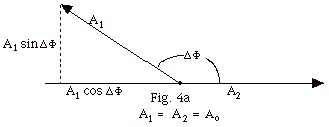
  1. A2 = [(A2 + A1 cos DF)2 + (A1 sin DF)2]
    A2 = A22 + 2A2A1 cos DF + A12 cos2 DF+ A12 sin2 DF
    A2 = A22 + 2A2A1 cos DF + A12 = 2Ao2(1 + cos DF)
    A2 = 2Ao2(2 cos2 DF/2)
    A2 = 4Ao2 cos2 DF/2.

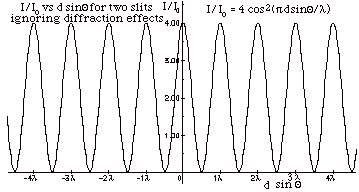
  2. I/Io = (A/Ao)2 = 4 cos2 DF/2.   I = Io cos2 DF/2,
    where DF/2= pd sin Q/l.

10.


  1. For direction (a) the waves from each antenna travel the same distance to a distant point. The path difference and the phase difference are zero.
    A = 3Ao  and  I = 9Io.  Fig. for 10(a)

  2. For direction (b) the path difference between the wave from antenna 2 and 3 is 90 m sin 30o = 45 m = l/4.
    DF = 2p(path difference)/l= 2p(l/4)/l= p/2. The path difference between antenna 1 and 3 is 180 m sin 30o = 90 m = l/2.
    DF= p.  A = A2 = Ao.  I = Io.  Fig. for 10(b)

  3. For direction (c), the path difference between the wave from antenna 2 and 3 is 90 m = l/2.
    DF =2p(path difference)/l= 2p(l/2)/l= p. The path difference between antenna 1 and 3 is 180 m = l.
    DF= 2p.  A = A3 - A2 + A1 = Ao.  I = Io.  Fig. for 10(c)

11.



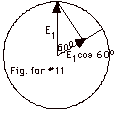
When the unpolarized light goes through the first polarizer, its irradiance drops by a factor of two.  With Io = 1000 W/m2,  I1 = 500 W/m2.  When it passes through the second polaroid, I2 = I1 cos2 60o = 500 W/m2 (1/4) = 125 W/m2.

12.



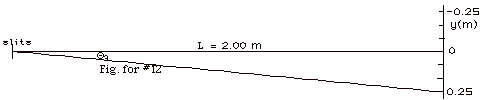
  1. For constructive interference ml = d sin Qm,  where m is an integer
    = 0, 1, 2, 3 . . . .,  l is the wavelength of the light, d is the distance between the sources or slits, and Qm is the angle for the mth maximum. Thus sin Q3 = ml/d = 3(656 x 10-9 m)/(1.57 x 10-5 m) = 0.125.  Q3 = 7.2o.

  2. For small angles sin Q ≈ tan Q ≈ y/L.
    Thus y3 ≈ LQ3 = 2.00 m(0.125) = 0.25 m.

13.

In general, lo = c/f, where f is the frequency of the light and lo and c are the wavelength and the speed of light in a vacuum or approximately in air, respectively. The frequency is a property of the source and not of the medium. When a wave enters a different medium, its wavelength and speed change, but its frequency remains the same. For a film with index of refraction n, the wavelength ln = v/f = (c/n)/f = (c/f)(1/n) = lo/n, since n = c/v  or  v = c/n.

14.



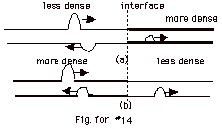
When a pulse goes from a less to denser medium, the reflected wave experiences a 180o or p phase change. When it goes from a more to less dense medium, there is no change of phase for the reflected wave. (Fig. for #14). From a crest to a trough is a distance of l/2. A change of phase of 180o or p is equivalent to a path difference of l/2. Notice that there is never a change of phase for the transmitted ray at an interface. The speed of light is greatest in a vacuum or approximately air with index of refraction n = 1 = c/v. The higher the index of refraction, the smaller the speed in the medium. When light goes from medium 1 to medium 2, the reflected ray will experience a phase change of p if n2 > n1.  There will be no phase change if n2 < n1.

15.

ym = mlL/d  or
m = ymd/Ll= (1.50 x 10-3 m)(1.00 x 10-3 m)/(1.00 m)(500 x 10-9 m) = 3.

16.

Dy = lL/d.

The distance between maxima Dy is directly proportional to the wavelength l and inversely proportional to the distance d between the slits. If the wavelength is halved, the distance between maxima is halved. If the distance between the slits is doubled, the distance between maxima is halved. The combination means the distance between maxima is reduced by a factor of four.

Dy’ = Dy/4.

17.

The distance between maxima Dy is directly proportional to the wavelength l. The wavelength of light in water ln of index of refraction n equals the wavelength lo in air or a vacuum divided by n.  Since n > 1,  ln is less than lo and the distance between maxima is smaller when the interference pattern is observed under water.

18.



The distance from A to B is 5.00000 cm. The path from A to the mirror to B is 1.60010 cm + 3.40020 cm = 5.00030 cm.

The difference in path is (5.00030 cm + l/2) - 5.00000 cm = 0.00030 cm + l/2.

The addition of l/2 to the path from A to the mirror to B occurs because of the change of phase of p when the light is reflected from the mirror. For a minimum at B, the path difference = 0.00030 cm + l/2 = (m + 1/2)l  or  0.00030 cm = ml.

For m = 1,  l= 0.00030 cm = 30 x 10-7 m.
For m = 2,  l= 0.00015 cm = 15 x 10-7 m.

19.



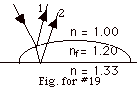
When the light goes from air to oil, the reflected wave 1 experiences a change of phase of p. The light that enters the oil is partly reflected at the oil-water interface. Again at this interface, the reflected wave experiences a change of phase of p, but it has no change in phase as it goes from the oil back into the air as the transmitted ray 2. The change of phase are additive. For both reflections, the total change of phase is p + p = 2p, which is equivalent to no change in phase.

There is, however a path difference as the ray travels down and back up in the oil. For almost normal incidence we say the thickness of the oil there is d and the path difference
2d = mlf,  m = 0, 1, 2, 3 . . . for constructive interference,   or

2d = (m + 1/2)lf,  m = 0, 1, 2, 3 . . . for destructive interference,
where lf is the wavelength of the light in the film.
  1. For the outer or thinnest regions of the drop, d approaches zero and there is no overall phase change or thickness so there is a maximum intensity of light.

  2. For a maximum 2d = mlf = mlo/nf.
    Thus possible d's are do = 0,  d1= 1(580 nm)/2(1.20) = 242 nm.
    d2 = 2(580 nm)/(2)(1.20)= 484 nm, etc.

20.





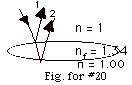
Now there is a change of phase at the interface between the air and the soap film so that ray 1 is reflected with a change of phase of p.  But there is no change of phase at the second film-air interface because now the ray is going from nf to n, where nf > n.  This is similar to adding (or subtracting) a path difference of lf/2.

For constructive interference, the path difference = 2d = (m + 1/2)lf    or
d = (m + 1/2)lo/2nf .

  1. For m = 2, a maximum occurs for d = (2 + 1/2)(580 nm)/2(1.34) = 541 nm.

    A minimum occurs for a path difference = 2d + lf/2 = (m + 1/2)lf,  or
    2d = mlf, which would have been the condition for a maximum had there been no change in phase of the reflected ray.

    Now for a minimum, d = mlf/2 = mlo/2nf.

  2. For m = 2, a minimum occurs for d = 2(580 nm)/2(1.34) = 433 nm.

21.

The sound is diffracted as it goes through the "slit" of the door with the longer wavelengths "bent" the most around the "slit". These wavelengths will be accentuated. The longer wavelengths correspond to lower-frequency notes.

22.

The wavelengths of sound are much greater than the wavelengths of visible light. Thus it is much easier to detect interference and diffraction properties of sound waves.

23.



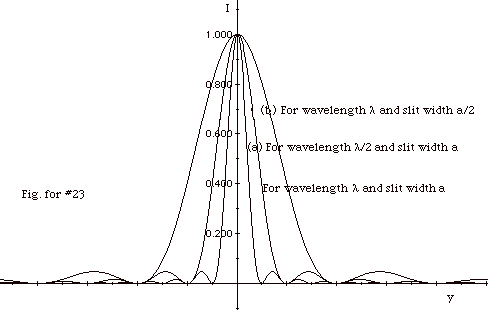
For small angles, the position of the minima ym’  is directly proportional to the wavelength l and inversely proportional to the slit width a.
  1. When the wavelength is halved, but slit width remains the same, the first minimum is closer to the central maximum and the distance between minima is smaller (Fig. for #23a).

    y1 for (a) is half the original y1 and the distance between minima Dy for (a) is half the original Dy.

  2. When the slit width is halved, but wavelength remains the same, the first minimum is further from the central maximum and the distance between minima is greater (Fig. for #23b).

    y1 for (b) is twice the original y1 and the distance between minima Dy for (b) is twice the original Dy.

24.



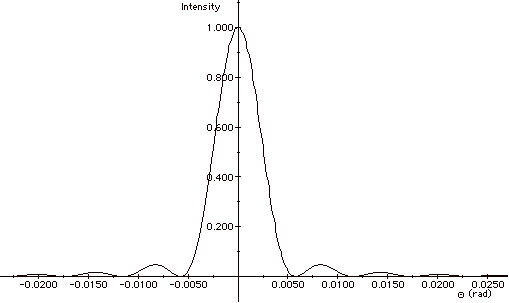
For a minimum sin Qm’ = m’l/a.
For m’ = 1,  the width of the slit a = 1.00 x 10-4 m and
l = 580 x 10-9 m, sin Q1 = 1(580 x 10-9 m)/10-4 m = 0.00580 ≈ Q1.
The width of the central maximum ≈ 2LQ1 = 2(2.0m)(0.0058) = 2.32 x 10-2 m. Plot of the intensity as a function of angle is shown in the figure above.

25.


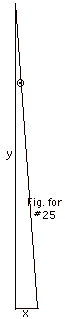
The angular limit of the resolution for the terrestrial telescope =
Qa = 1.22l/D = (1.22)(550 x 10-9 m)/(6.5 x 10-2 m) = 1.03 x 10-5.

In Fig. for #25 above (not to scale),  tan Q= x/y = x/1000 m,
where x equals the minimum distance of separation and y equals the distance from the objects.

For small angles the tangent of the angle is approximately equal to the angle in radians.
1.03 x 10-5 = x/ 1000 m   or
x = (103 m)(1.03 x 10-5) = 1.03 x 10-2 m = 1.03 cm.

26.

In general for a maximum,  sin Qm = ml/d.

In this problem,  d = 1 divided by the number of lines per meter
= 1/(2.00 x 105/m) = 5 x 10-6 m.

For  l= 653.4 x 10-9 m  and  m = 1,
sin Q1 = (1)(653.4 x 10-9 m)/(5 x 10-6 m) = 0.131 and Q1 = 7.51o.

For  l= 653.4 x 10-9 m  and  m = 3,
sin Q1 = (3)(653.4 x 10-9 m)/(5 x 10-6 m) = 0.393 and Q3 = 23.1o.

For  l= 580.8 x 10-9 m  and  m = 1,
sin Q1 = (1)(580.8 x 10-9 m)/(5 x 10-6 m) = 0.116 and Q1 = 6.67o.

For  l= 580.8 x 10-6 m  and  m = 3,
sin Q1 = (3)(580.8 x 10-9 m)/(5 x 10-6 m) = 0.348 and Q3 = 20.4o.

For the first order, the angular separation for the a and b lines is
(7.51 - 6.67)o = 0.84o.

In the third order, the angular separation for the a and b lines is
(23.1 - 20.4)o = 2.7o.

You get greater angular separation of the lines in the higher orders.

27.
  1. In general for a maximum,  sin Qm = ml/d.
     For two lines that are adjacent,  the m's differ by 1.

    Let m be the order for sin Q = 0.2  and  m + 1  the order for sin Q= 0.3.

    Then,
    0.2d = ml                      (Equation 1)
    0.3d = (m + 1)l                        (Equation 2)
    Eq. 2 - Eq. 1 gives
    0.1d = l   or
    d = l/0.1 = 600 x 10-9 m/0.1 = 6.0 x 10-6 m.


  2. Minima of diffraction patterns occur for a sin Qm’ = m’l, where a is the slit width. Since the fourth order interference maxima is missing it must fall at one of these angles. If a is the smallest slit width for which this order is missing, the order must correspond to m’ = 1 and the angle is given by sin Q1  = (1)l/a. This angle is also given for m = 4 for the interference pattern by sin Q4 = 4 l/d.

    Thus l/a = 4 l/d   or  a = d/4 = (6 x 10-6 m)/4 = 1.5 x 10-6 m.

  3. First set Q = 90o and find the largest value of m for which ml < d sin Q. This is the highest order that is diffracted toward the screen. The condition is the same as ml < d  or  m < d/l = 6 x 10-6 m/600 x 10-9 m = 10.  The highest order seen is  m = 9.  The fourth and the eight order are missing so the observable orders are m = 0, 1, 2, 3, 5, 6, 7, and 9.

  4. The intensity at the screen is given by  I = Io (cos2b) (sin a/a)2
    where  a = (pa/l)sin Q  and  b = (pd/l)sin Q,  and  Io is the intensity of the central maximum.  For the third bright line d sin Q = 3l,  so b = 3p  and  cos2 b = 1.

    a = 3pa/d = 3p/4.   (sin a/a)2 = [(sin 3p/4)/3p/4]2 = 0.090.
    I = 0.090Io.

28.

  I = Io cos2 Q.
  I/Io = 1/2 = cos2 Q.
  cos Q = (1/2)1/2.
  cos-1 (1/2)1/2 = 45o

29.
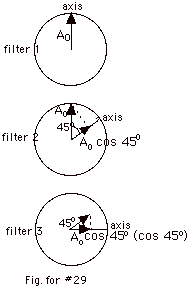After going through the first filter, the light has an amplitude of Ao and its polarization is vertical. When this light goes through the second filter that is at an angle of 45o with the axis of the first filter, the amplitude is the projection of Ao on the new axis which is Ao cos 45o. The third filter is at an angle of 90o with the first filter, but at an angle of 45o with the second filter. After passing through the third filter, the amplitude is
Ao cos 45o(cos 45o) =
Ao cos2 45o =
Ao [(1/2)1/2]2 =
Ao/2.
The intensity is proportional to the amplitude square.

I/Io = (Ao/2)2/Ao  or  I = Io/4 = 25% Io.

30.

Let  n1 = 1  and  n2 = 2.42.
tan Q1 = 2.42.   Q1 = 67.6o.

31.

Since the polarizing angle found in #30 was 67.6o  it can't be diamond.
tan 62.5o = 1.92,  which is the index of refraction of zircon.

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
August 8, 2002
March 16, 2003