|
Answers - Potential Energy, Potential,
and Capacitors
|
|
|
1.
|
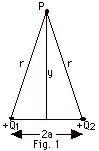
- The distances from Q1 and Q2 to
P are r = (y2 + a2)1/2.
Since V is a scalar quantity, the potentials add algebraically.
V = k(Q1/(y2 + a2)1/2
+ Q2/(y2 + a2)1/2)
= k(Q1 + Q2)/(y2 + a2)1/2.
Since a is a constant, V is a function only of y.
- For y2 >> a2, V = kQ/y,
where Q = Q1 + Q2 which is the same
as the potential due to a point charge Q located at the
origin.
|
|
|
2.
|
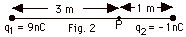
- The potential V is a scalar quantity. In this case you
may use a minus sign to calculate the potential. For a point
charge Q, the potential at a point P a distance r from P
is V = (9 x 109 N-m2/C2)Q/r.
For q1, V1 = (9 x 109
N-m2/C2)(9 x 10-9 C)/3
m = 27 N-m/C
= 27 J/C = 27 V.
For q2, V2 = (9 x 109
N-m2/C2)(-1 x 10-9
C)/1 m = -9 V.
V at P = (27 - 9) V = 18 V.
- The potential at P is really the potential difference
between point P and a very large distance from P. At an
infinite distance, the potential due to q1 and
q2 is zero (r = a very large number), V∞
= 0. The work done to bring a charge q3 from
a very great distance to P is the increase of the potential
energy of the system. The potential difference VP∞
= the potential energy difference divided by q3 =
(UP - U∞)/q3.
Work done = q3VP∞ = q(VP
- V∞)= ( 3 x 10-9 C)(18
J/C - 0) = 54 nJ.
- For q2 = +1 nC,
V1 = (9 x 109 N-m2/C2)(9
x 10-9 C)/3 m = 27 N-m/C = 27 J/C = 27 V.
V2 = (9 x 109 N-m2/C2)(1
x 10-9 C)/1 m = 9 V.
V at P = (27 + 9). V = 36 V.
Now the work done = q3(VP - V∞)
= ( 3 x 10-9 C){(36 J/C) - 0} = 108 nJ.
|
|
|
3.
|
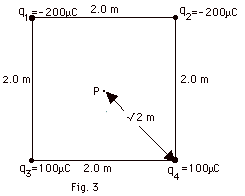
- In general, the potential due to a point charge Q at a
distance r is kQ/r.
For q1 = q2 = -200 x 10-6 C,
the potential at P is:
V = 9 x 109 N-m2/C2(-2
x 10-4 C)/√2 m
= -12.73 x 105 N-m/C
= -12.73 x 105 J/C
= -12.73 x 105 V.
For q3 = q4 = 100 x 10-6
C, the potential at P =
V = 9 x 109 N-m2/C2(10-4
C)/√2 m = 6.36 x 105 V.
Due to all the charges,
V = 2(-12.73 + 6.36)105 V
= -12.7 x 105 V.
- Work to bring q5 = 20 x 10-6 C from
infinity =
q5(VP – V¥)
= 20 x 10-6C(-12.7 - 0)105 V = -25.4
J.
|
|
|
4.
|
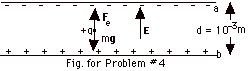
- The parallel plate capacitor with its charge and the particle
with the forces acting on it are shown in the figure above.
For the particle to be at rest, the net force acting
on it must equal zero: Fnet = ma = m(0).
Taking up to be positive, Fe - mg = 0
or Fe = mg, where the electric force on the particle
with charge q in an electric field E is Fe =
Eq. Thus,
Eq = mg or
E = mg/q = (10-3 kg)(9.8 m/s2)/(10-6
C) = 9.8 x 103 N/C.
The direction of the electric field is up. Remember
the direction of the electric field is that in which a positive
charge is urged.
- Vab = Ed = 9.8 x 103 N/C (10-3
m) = 9.8 J/C = 9.8 V.
|
|
|
5.
|

This is a problem in conservation of energy. The potential of
a sphere of charge equals the potential of a point charge =
kQ/r. When the alpha particle is a long distance away from the
gold nucleus initially i, the potential energy of the system
Ui is 0.
When the alpha particle touches the gold nucleus, r = 7.0 x
10-15 m = the radius of the gold nucleus. The
potential energy for the "final" position Uf
equals:
(9 x 109 N-m2/C2)(79)(2)
x (1.6 x 10-19 C)2/(7.0 x 10-15
m)
= 5.2 x 10-12 J.
From conservation of energy,
Ui + Ki = Uf + Kf
0 + Ki =
5.2 x 10-12 J + 0
|
|
|
6.
|
Ui +
Ki = Uf
+ Kf or
Ui - Uf = q(Vi - Vf)
= 1/2 mvf2 - 1/2 mvi2
1.6 x 10-19 C(100 J/C) = 1/2(1.67 x 10-27
kg)vf2 - 0
vf = (2 x 1.6 x 10-17 J/1.67 x 10-27
kg)1/2 = 1.38 x 105 m/s
|
|
|
|
|
8.
|
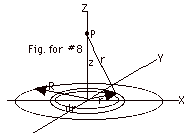
- dA = 2pr dr
- dq = s dA = 2psrdr
- dV = kdq/r = 2pskrdr/(z2
+ r2)1/2
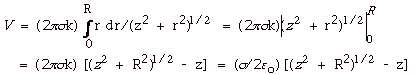
-
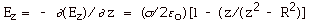
|
|
|
9.
|
- VA = 9.0 x 109 N-m2/C2[80/0.10
- 60/0.10]10-9C/m =1.8 x 103 V
- VB = 9.0 x 109 N-m2/C2[80/0.16
- 60/0.12]C/m = 0
- WB
 A
= q(VA - VB) = (10 x 10-6
C)(1.8 x 103 V) = 0.018 J. A
= q(VA - VB) = (10 x 10-6
C)(1.8 x 103 V) = 0.018 J.
|
|
|
10.
|
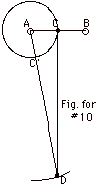 |
In the field of these
charged wires, draw the circular equipotential traces
passing through C and D. The electric field
due to the wire through A or B = l/2peor,
where r is the distance from the wire to the field points.
The direction of the field is radially away from the wire.
|
First consider the wire passing though A:
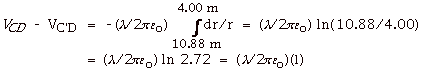
In the field of both wires, the potential difference is twice
as large, or
l/2peo(2)
= l/pe
|
|
|
11.
|
- When capacitors are wired in parallel, the equivalent
capacitance
C = C1 + C2 + C3
But C1 = C2 = C3 = eoA/d
so C = 3eoA/d
= eoA/(d/3)
The plate spacing for the single capacitor must be d/3.
- When capacitors are wired in series, the reciprocal
of the equivalent capacitance
1/C = 1/C1 + 1/C2 + 1/C3
= 3/C1 and
C = C1/3 = (eoA/d)/3
= eoA/3d
so the plate spacing for the single capacitor must be 3d.
|
|
|
12.
|
For any capacitance, including C1,
C1 = Q/(Vab)i,
where Q is the charge on the capacitor when (Vab)i
is the potential difference across it.
When the two capacitors are wired in parallel, the potential
difference across each is the same =
(Vab)f = q1/C1
= q2/C2,
where q1 and q2 are the charges on C1
and C2 with potential difference (Vab)f.
Also from conservation of charge
q1 + q2 = Q, or
q2 = Q - q1 = C1 (Vab)i
- C1 (Vab)f = C1{(Vab)i
- (Vab)f}.
But q2 also equals C2 (Vab)f.
Thus,
C1{(Vab)i - (Vab)f}
= C2(Vab)f, or
since C1
= 4peoR1
and
C2 = 4peoR2,
4peoR1
{(Vab)i - (Vab)f}
= 4peoR2(Vab)f,
so
R2 = R1{(Vab)i
- (Vab)f}/(Vab)f.
|
|
|
13.
|
The capacitance of a parallel plate capacitor
in a vacuum C = eoA/d,
where A is the area of the plates and d is the distance between
them.
- When the plate separation is doubled:
- The capacitance C is halved since the capacitance
is inversely proportional to the distance d.
- C = Q/Vab or Q = CVab.
When C is halved and Vab remains the
same (the battery is still across the capacitor), the
charge Q is halved.
- E = s/eo.
When Q is halved, the charge per unit area s
is halved and E must be halved. Also E = Vab/d
so when d is doubled E is halved.
- When a dielectric with k=
2 is inserted:
- The capacitance = keoA/d
so the capacitance is doubled.
- Q = CVab. When the capacitance doubles,
with constant Vab, the charge doubles.
- E = s/keo.
When Q doubles, s
doubles, but s/k
remains the same because k
= 2 and E remains the same. Also E = Vab/d
so E is the same because Vab and d
remain the same.
|
|
|
14.
|
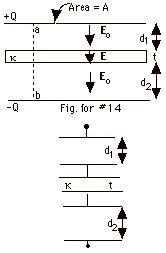
The electric field in the air gaps is - Eoj
= - s/eo
j= - Q/Aeo
j.
The electric field in the dielectric is - Ej = - Q/Akeo
j.
Vab = - a∫b E
. dyj = (Q/Aeo)(d1
+ t/k + d2).
C = Q/Vab = Aeo/(d1
+ t/k + d2).
Alternatively, we may view the capacitor as three capacitors
in series, shown in the lower portion of the figure above.
For series 1/Ceq = 1/C1 + 1/C2
+ 1/C3 = d1/Aeo
+ t/Akeo + d2/Aeo.
Ceq
= Aeo/(d1
+ t/k + d2).
|
|
|
15.
|
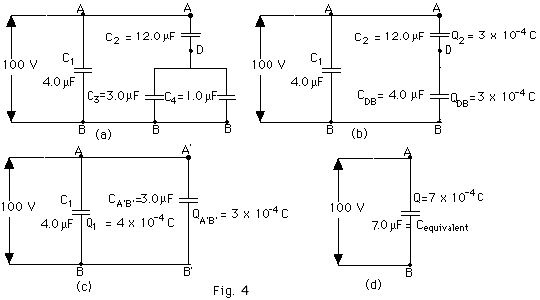
- We find the equivalent capacitance by starting with the
parallel combination between D and B. Capacitors in
parallel add.
CDB = C3 + C4 = (3.0 +
1.0)µF = 4.0 µF (Fig. 4b ).
CDB and C2 are in series. The reciprocal
of the equivalent capacitance equals the sum of the reciprocals
of the capacitors in series.
1/CA’B’ = 1/C2 + 1/CDB
= 1/12 µF + 1/4.0 µF = (1 + 3)/12 µF or
CA’B’ = 3.0 µF (Fig. 5c).
Then C1 and CA’B’
are in parallel.
Cequivalent = (4.0 + 3.0) µF = 7.0 µF.
- Now to find the charges and potential differences we
work backwards.
For Fig. 4d,
VAB = 100V = Qequivalent/Cequivalent
= Qequivalent/7.0 x 10-6 C/V.
Qequivalent = 7.0 x 10-4 C.
For Fig. 4c,
VAB = 100V = Q1/C1
= Q1/4.0 x 10-6 C/V. Q1
= 4.0 x 10-4 C.
QA’B’ = 100 V(CA’B’)
= 100 V (3.0 x 10-6 C/V) = 3.0 x 10-4
C.
Notice Q1 + QA’B’ = 7.0
x 10-4 C.
For Fig. 4b, C2 and CDB are in series
and have the same charge.
Q2 = QDB = QA’B’
= 3.0 x 10-4 C.
- VAD = Q2/C2 = 3.0 x
10-4 C/12 x 10-6 C/V = 25 V.
VDB = QDB/CDB = 3.0 x 10-4
C/4 x 10-6 C/V = 75 V.
Notice VAD + VDB = 100 V.
Q3 = C3 VDB = 3.0 x 10-6
C/V (75 V) = 2.25 x 10-4 C.
Q4 = C4 VDB = 1.0 x 10-6
C/V (75 V) = 0.75 x 10-4 C.
Notice that Q3 + Q4 = 3.0 x 10-4
C = Q2.
- Energy stored in a capacitor = U = 1/2 QV = 1/2 Q2/C.
U1 = 1/2 Q12/C1 =
1/2(4.0 x 10-4 C)2/(4.0 x 10-6
C/V) = 2.0 x 10-2 J.
U2 = 1/2 Q22/C2 =
1/2(3.0 x 10-4 C)2/(12.0 x 10-6
C/V) = 0.375 x 10-2 J.
U3 = 1/2 Q32/C3 =
1/2(2.25 x 10-4 C)2/(3.0 x 10-6
C/V) = 0.843 x 10-2 J.
U4 = 1/2 Q42/C4 =
1/2(0.75 x 10-4 C)2/(1.0 x 10-6
C/V) = 0.281 x 10-2 J.
U1 + U2 + U3 + U4
= 3.5 x 10-2 J.
Uequivalent = 1/2 (Qequivalent)2/Cequivalent
= 1/2(7 x 10-4 C)2/(7 x 10-6
C/V) = 3.5 x 10-2 J.
|
|
|
|
|
17.
|
From Gauss' theorem, we found that the
electric field a distance r from the axis of a cylinder equals
2kl/r, where l
is the charge per unit length. For a cylinder of total
charge Q and length L, l=
Q/L and E = 2kQ/rL. In this problem, we have coaxial cylinders
of radius a and radius b with b > a. Using Gauss's
theorem, the electric field between the cylinders still equals
2kQ/rL because a Gaussian surface there does not enclose the
charge on the outer cylinder.
- By definition,
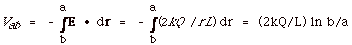
- C = Q/Vab = Q/[(2kQ/L) ln b/a] = L/[2k (ln
b/a)].
|
|
|
18.
|
To move the plates a distance ds, takes
dW = F ds, where F is the force we are seeking.
- The energy stored in the electric field is U = (1/2)Q2/C.
For a parallel plate capacitor of area A and separation
s,
C = eoA/s
and
U = Q2s/2eoA,
where Q, eo,
and A are constants.
- The work dW would appear as an increase dU in the potential
energy:
dU = (Q2/2eoA)ds
Equating dW and dU, we find
F ds = (Q2/2eoA)ds
and
F = (Q2/2eoA).
|
|
|
19.
|
- q = (charge/volume)(volume) = r(4pr3/3)
- q’ = r(4pr2
dr)
- dU = kqq’/r = kr2(4p)2r5
dr/3r
- U = kr2(4p)2/3
o∫R r4 dr = kr2(4p)2
R5/15 = 3k(4pR3r/3)2/5R
= 3kQ2/5R, where the total charge of the sphere
of radius R is Q = (4pR3r/3).
|
|
|
20.
|
3kQ2/5ro = mc2.
ro = 3kQ2/5mc2
= 3(9.0 x 109 N-m2/C2)(1.6
x 10-19 C)2/5(9.1 x 10-31
kg)(3.0 x 108 m/s)2
= 1.7 x 10-15 m.
|
|
|
21.
|
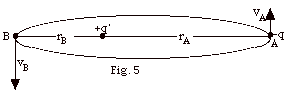
- From conservation of angular momentum,
LA
= LB
rAmvA sin 90o =
rBmvB sin 90o
vB/vA = rA/rB
= 6 x 10-5/3 x 10-5 = 2
- From conservation of energy,
UA +
KA =
UB +
KB
-kqq’/rA + 1/2 mvA2
= -kqq’/rB + 1/2 mvB2
-kqq’/rA + kqq’/rB
= 1/2 mvB2 - 1/2
mvA2
kqq’(1/rB - 1/rA) =
m/2(vB2 - vA2)
= m/2(4vA2 - vA2)
= 3mvA2/2
9 x 109 N-m2/C2(10-6
C)(10-6 C)(105/m)[1/3 -1/6]
= 3(10-10 kg)vA2/2
vA = 106 m/s
vB = 2vA = 2 x 106 m/s
|
|
|
22.
|
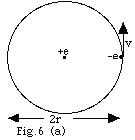 |
- U = -ke2/r
- Fnet = ma
ke2/r2 = mv2/r or
mv2 = ke2/r
- E = U + K
= -ke2/r + 1/2 mv2
= -ke2/r + 1/2 ke2/r
= -ke2/2r
L = mvr
|
|
|
|
|
|
|
|
25.
|
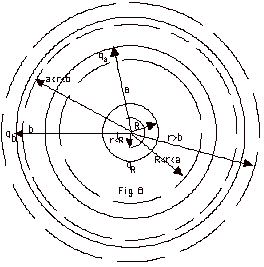
In general, 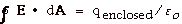
In all cases, E is constant over the Gaussian surface
and the angle between
E and dA is zero.
Thus, 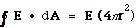 .
.
- For a < r < b, the dashed Gaussian surface
is inside a conductor so the electric field is zero. The
charge enclosed must be zero or
0 = qR + qa and
qR = - qa = -5 µC.
- For 0 < r < R, the Gaussian surface
is again inside a conductor and E = 0.
For R < r < a, the charge enclosed is
qa.
E4pr2 = qR/eo.
E = -5 x 10-6C/4peor2
= k(-5 x 10-6C/r2).
The minus sign means the electric field for R <
r < a is radially inward.
For a < r < b, as we said before, E
= 0.
For r > b, the charge enclosed = qR
+ qa + qb = qb since
qR = - qa.
E4pr2 =qb/eo.
And E = qb/4peor2
= kqb/r2.
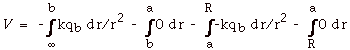
For r >b, V(r) = kqb/r.
For a < r < b, V(r) = kqb/b.
For R < r < a, V(r) = kqb/b
- kqa(1/r - 1/a).
For r < a, V(r) = kqb/b - kqa(1/R
- 1/a).
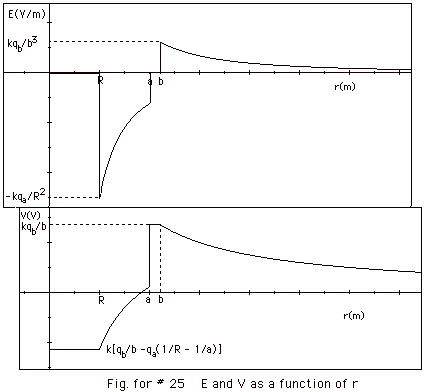
Plots of E and V as a function of r are below in Fig. for
25.
|
|
|
26.
|
- E(r) = l/2peo
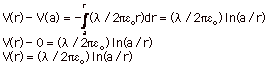
- ln ∞ ≠ 0. With an infinite wire you
can't get away with choosing V = 0
at infinity.
- E = -dV/dr = -d{(l/2peo)(ln
a – ln r)/dr = l/2peor!
|
|
|
27.
|
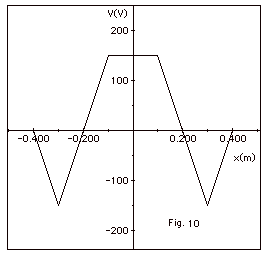
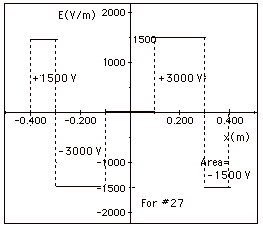
E = - dV/dx
or
E = - slope of V vs
x
For –0.4 m < x < -0.3 m,
- Slope = - (-150 – 0)V/{(-0.3 –(-0.4)}m
= +1500 V/m.
For –0.3 m < x < -0.1 m,
- Slope = -{150 – -(150)}V/{(-0.1 –(-0.3)}m
= -1500 V/m.
For –0.1 m < x < 0.1 m,
slope = 0.
For 0.1 m < x < 0.3 m,
- slope = -(-150 – 150)V/(0.3 –0.1)}m
= +1500 V/m.
For 0.3 m < x < 0.4 m,
- slope = -{0 – (-150)}V/(0.4 –0.3)}m
= -1500 V/m.
If you are so inclined, you can work backwards.
V – 0 = -∫ E dx or
V = - area under E vs
x.
For example, - the area from x = 0.40 m
to x = 0.3 m is 150 V.
V(0.3m) = 0 –150 V = - 150 V. Try it
for a few other points.
|
|