|
|
|
1.
|
Write an expression for (a) the distance
x moved by a particle traveling with a constant linear velocity
v in time t and (b) the angle Θ
moved by a particle rotating with a constant angular velocity
ω in time t.
|
|
|
2.
|
Write an expression for (a) the constant
linear acceleration a of a particle going from linear velocity
vo at time t = 0 to a velocity v
at time t and (b) the constant angular acceleration going
from angular velocity ωo
at time t = 0 to angular velocity ω
at time t.
|
|
|
3.
|
Given that (a) dx/dt = v and a is constant,
find x(t) for an object initially at xo
traveling with vo at t = 0 and (b)
dΘ/dt = w and αis constant, find Θ(t)
for an object initially at Θo
and rotating with ωo
at t = 0.
|
|
|
4.
|
Starting from Θo = 0 and ωo
= π s-1,
a wheel is given a constant angular acceleration of 4 π
s-2. After 4.0 s find (a)
its angular speed and (b) how many turns the wheel has made.
|
|
|
5.
|
The angular position of a particle is
given by Θ(t) = b + ct + et2,
where b, c, and e are constants. Find (a) the angular velocity,
(b) the angular acceleration α,
(c) the linear velocity, (d) the tangential acceleration,
and (e) the centripetal acceleration of the particle at time
t = t1. The particle travels in
a circle of radius r.
|
|
|
6.
|
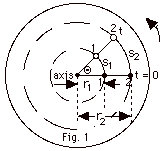
The wheel shown in Fig. 1 below rotates
with constant angular velocity ω.
Show that points 1 and 2 on the wheel move with the same angular
velocity, but different linear velocities. In Fig. 1, dark
circles show the initial positions of the two points and the
positions at time t are shown with open circles. Point 1 is
a distance r1 from the axis and
2 a distance r2 > r1
from the axis.
|
|
|
|
7.
|
Starting from rest at t = 0, a wheel
undergoes a constant acceleration from t = 0 to t = 10 s.
When t = 3.0 s, the angular velocity of the wheel is 6.0 rad/s.
Through what angle does the wheel rotate from t = 0 to t =
20 s.
|
|
|
8.
|
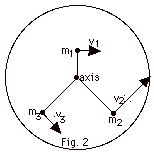
Some of the particles that make up the
rigid body of a disk are shown in Fig. 2 . (a) Write a summation
for the total kinetic energy of the disk with particles from
i = 1 to i = N in terms of the mass mi
of a particle and its velocity vi.
(b) Substitute the expression for the angular velocity ω
of the disk in terms of vi and ri.
(c) Take the 1/2 and ω out of the
summation and identify the quantity represented by the summation.
(d) Rewrite the kinetic energy in terms of 1/2, ω
and the quantity represented by the summation.
|
|
|
|
9.
|
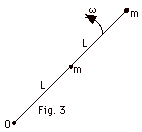
Two particles each of mass m are connected
by two very thin rods of length L and rotate about axis O
with a constant angular velocity ω
as shown in Fig. 3 below. Find (a) the moment of inertia and
(b) the kinetic energy of rotation of the system about O.
|
|
|
|
10.
|
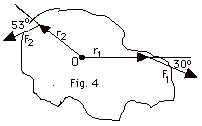
The object in Fig. 4 below is rotated
about the axis at O by two forces. Find the magnitude and
direction of the net torque on the object about O.
Given r1 = 2.0 m, F1
= 1.5 N, r2 = 1.0 m, F2
= 1.0 N.
|
|
|
|
11.
|
A thin rod of length L and mass m is
suspended at one end. It is pulled to one side and allowed
to swing like a pendulum. It passes through the lowest point
with an angular velocity ω. Find
(a) its kinetic energy as it passes through its lowest position
and (b) and the height to which its center of mass rises above
its lowest position.
|
|
|
12.
|
A pencil of length L, initially standing
on one end falls over. With what speed does the eraser strike
the horizontal surface, assuming the pencil point remains
at rest on the surface? Consider the pencil to be a thin rod.
|
|
|
13.
|
A uniform rod of length L and mass M
is free to rotate about a frictionless pivot at the end attached
to a wall. The rod is released from rest in the horizontal
position. Find the initial (a) angular acceleration
of the rod and (b) the linear acceleration of the right end
of the rod.
|
|
|
14.
|
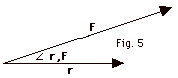
Show that |
τ | = rF sin  r,F
can be written as the product of the force times the component
of r perpendicular to F. r,F
can be written as the product of the force times the component
of r perpendicular to F.
|
|
|
|
15.
|
You wish to push a wheel of mass M and
radius R over a curb of height h by exerting a force F on
the axle of the wheel. Find the minimum force F required to
do the job.
|
|
|
16.
|
A particle of mass m moves in the xy
plane in a circular path of radius r. The motion of the particle
is counterclockwise. Find (a) the magnitude and direction
of its angular momentum relative to the center of the circle
when its velocity is v and (b) an alternative expression for
L in terms of the angular velocity ω.
|
|
|
17.
|
Show that the magnitude of the angular
momentum of a particle can be written as the product of (a)
the momentum of the particle p and the component its position
vector r perpendicular to p and (b) the position
vector r and the component of its momentum p
perpendicular to r.
|
|
|
18.
|
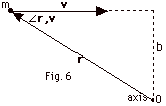
Find the direction and magnitude of the
angular momentum of the particle of mass m moving with velocity
v a distance r from the axis shown in Fig. 6
below.
|
|
 |
|
19.
|
A light rod 1.0 m in length rotates in
the xy plane about a pivot through the rod's center. Two particles
of mass 4.0 kg and 3.0 kg are connected to its ends (Fig.
7 below). Determine the angular momentum of the system about
the origin at the instant the speed of each is 5.0 m/s.
|
|

|
|
20.
|
An artificial satellite is held in an
elliptical orbit (Fig. 8) around the earth by the gravitational
force Fg. Find the ratio
of its velocity v1 at P1
a distance r1 from the earth to
its velocity v2 at P2
a distance r2 from the earth. Explain
your answer.
|
|
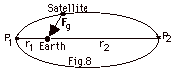
|
|
21.
|
A sphere of radius R rolls down an inclined
plane of height h and angle of inclination Θ.
Find (a) using conservation of energy, the velocity of the
center of mass when the sphere is at the bottom of the incline
and (b) using Fnet = ma and τnet
= Iα, (i) the acceleration
of the center of mass, (ii) the frictional force that acts
on the sphere, and (iii) the speed of the sphere at the bottom
of the incline. Isphere about center
of mass = 2/5 MR2.
|
|
|
22.
|
A uniform ladder of length L and weight
W = 50 N rests against a smooth, vertical wall. The smoothness
of the wall means that the force due to the wall is horizontal
and to the right, as shown in Fig. 9 below. If the coefficient
of static friction between the ladder and ground is µs
= 0.40, find the minimum angle Θmin
such that the ladder will not slip.
|
|

|
|
23.
|
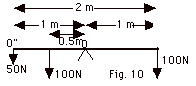
A uniform board with a weight of 40 N
and the applied forces shown in Fig. 10 below is in equilibrium.
(a) Show all the other forces acting on the board and indicate
their direction and magnitude. Explain your answer. (b) Take
the axis at O, the position of the fulcrum, and show that
the net torque acting on the board is zero. (c) Repeat
(b) for an axis about O" at the left end of the board.
|
|
 |
|
24.
|
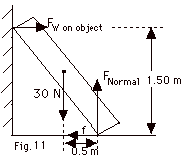
An object leans against a wall and remains
at rest, as shown in Fig. 11 below. Its weight of 30 N acts
at the center of gravity as shown in the figure. Find (a)
the normal force FNormal, (b) the force of the
wall on the object FWall on object
(c) the frictional force and (d) the coefficient of friction
between the floor and the object.
|
|
|