Answers - Two Dimensional Motion

1.

You find the resultant of two vectors graphically by (a) the parallelogram method or (b) the polygon method. In the parallelogram method, complete the parallelogram, as shown by the dashed lines in Fig. for #1a below. The resultant s is the diagonal. In the polygon method, move the tail of one of the vectors, for example s₁, to the head of s₂. The resultant s goes from the tail of s₂ to the head of s₁ (Fig. for #1b below in the statement of the problem).

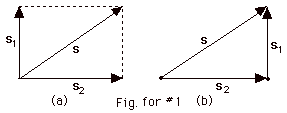
2.

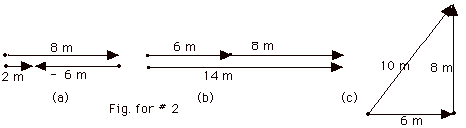
(a) For vectors along a straight line, you can assign a positive sign for a vector to the right and a negative sign for a vector to the left. Letting 8 m be to the right and 6 m to the left, 8 m - 6 m = 2 m. This is also shown in a vector diagram in Fig. for #2a below. Because the two vectors lie along the same straight line, I have drawn the vector for -6 m below the vector for +8 m. Remember two vectors are equal if they have the same magnitude and direction even if they do not start at the same point.

(b) Now let both 8 m and 6 m be to the right: 8 m + 6 m = 14 m. This is also shown in a vector diagram in Fig. for #2b below.

(c) Note that (8² + 6²)^1/2 = 10. If the vectors are at a right angle then the resultant vector has a magnitude of 10 m, as shown in a vector diagram in Fig. for #2c below.

3.

First find the components of A.

  A_x = A cos 37^o = 10 cm (0.8) = 8 cm
  A_y = A sin 37^o = 10 cm (0.6) = 6 cm

We are given that B_x = 8 cm and B_y = - 2 cm.

For C = A + 1/2 B,

  C_x = A_x + B_x/2 = (8 + 4) cm = 12 cm and C_y = A_y + B_y/2 = (6 - 1) cm = 5 cm.
  C = (12² + 5²)^1/2 cm = 13 cm.
  tan Θ = C_y/C_x = 5/12 = 0.42.   Θ = 26⁰.

Figure for #3 is shown below.

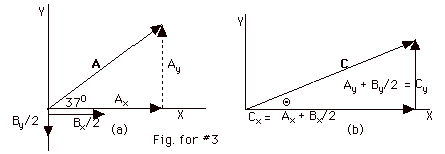
4.

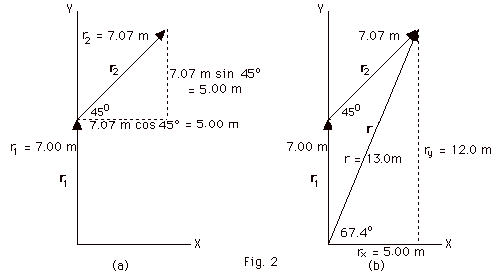
The vector r₁ is totally in the +Y-direction.
The component of r₁ along the X-axis, r_1x = r₂ cos 90⁰ = (7.00 m)0 = 0.
The component of r₁ along the Y-axis, r_1y = r₁ sin 90⁰ = 7.00 m (1) = 7.00 m. The component of r₂ along the X-axis, r_2x = r₂ cos 45⁰ = 7.07 m (0.707)
= 5.00 m.
The component of r₂ along the Y-axis, r_2y = r₂ sin 45⁰ = 7.07 m (0.707)
= 5.00 m.
The component of r along the X-axis, r_x = r_1x + r_2x = 0 + 5.00 m = 5.00 m.
The component of r along the Y-axis, r_y = r_1y + r_2y = 7.00 m + 5.00 m = 12.0 m.

(a) r = r_xi + r_yj = (5.00i + 12.0j) m.

(b) The magnitude of r = r = (r_x² + r_y²)^1/2 = (5.00² + 12.0²)^1/2 m = 13.0 m.
tan Θ= 12/5.  Θ= 67.4⁰.

See Fig. 2 below.

5.

For motion in the horizontal direction along the X-axis,
   t = x/v_x = 60 ft/(132 ft/s) = 0.454 s.

For motion in the vertical direction along the Y-axis,
   the vertical drop y = 1/2 at² = 1/2 (32 ft/s²)(0.454 s)² = 3.3 ft.

6.

(a) For horizontal motion of the rock,
                             x = 24 m/s t.                            (Equation 1)

      For horizontal motion of the car,
                    x = 90 m -1/2(4.0 m/s²)t²                (Equation 2)

      Substituting Eq. 1 into Eq. 2:
          24 m/s t = 90 m -1/2(4.0 m/s²)t²   or   t² + 12s t - 45s² = 0
           (t - 3s)(t + 15s) = 0   or   t = 3 s.

(b) Distance fallen by the rock = y = 1/2 at² = 1/2(10 m/s²)(9s²) = 45 m.

7.

For the vertical motion of the ball, y = 1.0 m = 1/2(10 m/s²)t² and t = 0.45 s. For the horizontal motion, x = v_xt = (4.0 m/s)(0.45 s) = 1.8 m.

8.

The expressions for the quantities t, y_max, v_y(t). and x will all remain the same. This is exactly what the principle of superposition is telling us. The object is subjected to two different influences, an initial velocity and a continuing acceleration due to gravity, and the object responds to each without altering its response to the other. The fact that the object has an initial horizontal velocity does not alter its vertical motion or the time it takes the object to hit the ground. The fact that the object is subjected to a vertical acceleration does not change its constant horizontal velocity motion. As a result you may separate a two-dimensional problem of a projectile into two one-dimensional problems.

9.

(a) At the initial position i, v_ix = v_o cos 37⁰ = 25 m/s (0.80) = 20 m/s and
v_iy = v_o sin 37⁰ = 25 m/s (0.60) = 15 m/s.

(b) At any time, the horizontal component of the velocity v_x = v_ix + a_xt =
v_ix + (0)t = 20 m/s. There is no acceleration in the x-direction and the object continues to move with a constant horizontal velocity. At the highest point, the vertical component of velocity is zero. It does not continue to move upward. It momentarily stops moving upward and then moves down. It does continue, however, to have the same constant horizontal velocity. Notice that this velocity at h is tangent to the path, as it should be.

(c) At f, the horizontal velocity still equals 20 m/s. It takes 3.0 s. to move 60 m (see x position of object just before it hits the ground in Fig. 3 below) at a constant horizontal velocity of 20 m/s. At t = 3.0 s, the vertical velocity v_fy(3.0s) = v_iy + a_yt = 15m/s + (-10 m/s²)(3.0 s) = -15 m/s. For this symmetrical situation, v_fy = -v_iy. The final velocity is 25 m/s at an angle of -37⁰. Notice also for this case where y_i = y_f = 0, the time to go half the distance horizontally equals one-half the total time of flight.

(d) The velocity at h and f are shown in Fig. 3 below.

(e) The acceleration is a constant. It is vertically downward and we took it to be -10 m/s². The acceleration vectors are shown at x = 20.0, 30.0, and 40.0 m in Fig. 3 below.

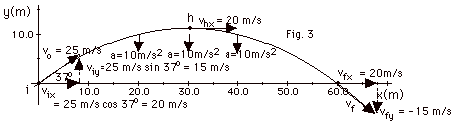
10.

Divide this problem into two one-dimensional problems:

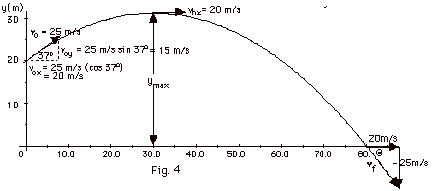
(a), (b), (f), and (g) are drawn on Fig. 4 below.

11.

To catch up to the ball, the horizontal velocity v_b of the boy must equal the initial horizontal velocity of the ball:

   v_b = v_ox = v_o cos Θ.    cos Θ = v_b/v_o = (20 m/3s)/20 m/s = 1/3.
   Θ = 70.5^o.    v_oy = v_o sin Θ = 20 m/s sin 70.5^o = 18.9 m/s.

For motion in the y-direction, v_y(y) = v_oy² + 2 a_y(y - y_o).

For the highest point, v_y = 0 and 0 = (18.9 m/s)² - 20 m/s²(y - y_o).
The ball rises (y - y_o) = (18.9)²m/20 = 17.8 m.

12.

Substituting Eq. 2 into Eq. 1:
180 m = (v_o cos )(2v_o sin Θ/a_y) = (2v_o² sin cos Θ/a_y), or
v_o² = 90 m a_y/sin Θ cos Θ     (Equation 3)

When the ball clears the tree,
x = 30 m = (v_o cos Θ)t and        y = 15 m = v_o sin Θ t - 1/2 a_yt² (Equation 4)
t = 30 m/(v_o cos Θ) (Equation 5)

Substituting Eq. 5 into Eq. 4:
15 m = (v_o sin Θ)(30 m/v_o cos Θ) - 1/2 a_y(30 m/v_o cos Θ)², or
15 m = 30 m tan - 1/2 a_y(30 m/v_o cos )²       (Equation6)

Substituting Eq. 3 into Eq. 6:
15 m = 30 m tan Θ - 1/2 a_y (30 m/cos Θ)²(sin Θ cos Θ/90 m a_y)
15 m = 30 m tan Θ - 5 m tan Θ= 25 tan Θ.
tan Θ = 15/25.  Θ= 31⁰.
v_o² = 90 m a_y/sin Θ cos Θ = 180 m a_y/sin 2Θ
= 180 m(10 m/s²)/0.88
v_o= 45 m/s.

13.

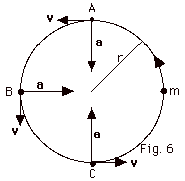
(a) and (b). The velocity v and the acceleration a at positions A, B, and C for an object moving with uniform circular motion are shown in Fig. 6 below. The magnitude of the velocity is a constant and always tangent to the circle at the point where you wish to find it. The centripetal acceleration is constant in magnitude and always in toward the center of the circle. The centripetal acceleration a = v²/r = (2.0 m/s)²/0.4 m = 10 m/s².

(c) While the magnitudes of the velocity and acceleration are constants, the directions are not. Thus neither v nor a is constant.

(d) A change in direction of velocity results in an acceleration just as much as a change in the magnitude of the velocity. You could use this device to see how many "g's" an object could withstand. For the radius and speed in this problem, the object is subjected to approximately 1g since 10 m/s²≈1 g.

14.

(a) The period = distance moved in one complete rotation/velocity

       = 2 πr/v = 2 π(0.4 m)/2.0 m/s = 0.4 π s.

(b) The frequency = 1/period = 2.5/ π s^-1

(c) From (a) v = 2 πr/T. The centripetal acceleration a = v²/r = (2 πr/T)²/r = 4 π²r/T² = 4 π²rf² = (d)