|
Answers - Simple Harmonic Motion
|
|
|
1.
|
|
(a)
|
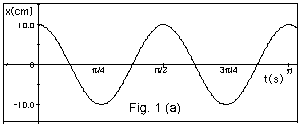
The maximum displacement from the
equilibrium position xm = 10.0 cm.
|
 |
|
(b)
|
The time for one complete oscillation
T = π/2 s. Notice
the maximum positive displacement
x = +10.0 cm occurs at t = 0 and the next time at t
= π/2 s.
It occurs again at
t = π s.
|
|
|
|
2.
|
|
(a)
|
v(t) =
-(2 π/T)(xm sin
2 πt/T). The maximum value
of the sine is 1. The maximum absolute value of v =
2 πxm/T. The ±
signs account only for the direction of the velocity.
|
 |
|
(b)
|
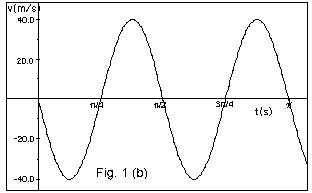
From Fig.1b, vmax =
40.0 cm/s = 2 πxm/T
=
2 π(10 cm)/( πs/2).
|
|
|
|
3.
|
|
(a)
|
(i) a(t) =
-(2 π/T)2(xm
cos 2 πt/T). Maximum
value of cosine is 1.
amax = (2 π/T)2xm.
The ± signs account for the direction of acceleration.
(ii) a(t) =
-(2 π/T)2
(xm cos 2 πt/T)
= -(2 π/T)2
x(t), since x(t) = xm cos 2 πt/T.
-a(t)/x(t) = (2 π/T)2.
|
 |
|
(b)
|
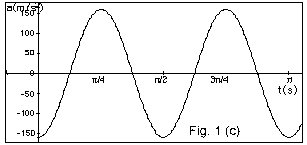
From Fig.1c, amax =
160 cm/s2 = (2 π/T)2xm
= (2 π/( π
s/2)210cm.
|
|
|
|
4.
|
(a) For a mass attached to a spring,
F = -kx or F/x = -k, where k is
a constant. The applied force F is directly proportional
to the displacement x and the minus sign says it is
in the opposite direction to x.
(b) When the spring is extended and released, Fnet =
ma or -kx = ma or -a/x = k/m.
|
|
|
5.
|
From 3a(ii), -a(t)/x(t) = (2 π/T)2.
From 4b, -a/x = k/m.
By comparison, k/m = (2 π/T)2
or T= 2 π(m/k)1/2.
|
|
|
6.
|
(a) Given x(t) = xm cos (2 πt/T +φ), where xm is the maximum displacement
from the equilibrium position. Maximum value of cos (2 πt/T +φ) is 1. The equation accurately describes
the definition of xm.
(b) x(t + T) =xm cos [2 π(t
+ T)/T +φ] = xm
cos T/T +φ] =
A cos [2 πt/T
+ 2π + φ]
= xm cos (2 πt/T +φ) = x(t). T is accurately described by
the equation of motion for simple harmonic motion xm
cos (2 πt/T +φ). It allows for the value of x at t to equal
x at t + T or t + nT,
where n = 1, 2, 3 . . . .
(c) For x(t) = xm cos (2 πt/T
- π/2), x(0) = xo
= xm cos (- π/2)
= 0.
v(t) = -(2 π/T)xm
sin (2 πt/T - π/2).
v(0) = vo = -(2 π/T)xm
sin ( - π/2) = (2 π/T)xm
= +vmax
At t = 0, the object is at the equilibrium position and travelling
with the maximum velocity in the +X-direction.
|
|
|
7.
|
|
In general,
x(t) = xm
cos (2 π t/T + φ),
and
v(t) = dx/dt
= -xm(2 π/T) sin
(2 π t/T + φ)
|
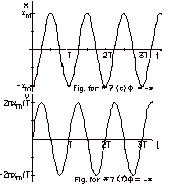
|
|
(a)
|
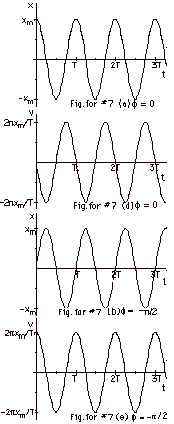
In Fig. for #7a, x(t) is plotted
for φ = 0, and
|
|
(d)
|
in Fig. for #7d, v(t) is plotted
for φ = 0.
For φ = 0 and t = 0 , the
initial conditions are: the initial displacement = xo
= xm and the initial velocity = vo
= 0. Immediately after t = 0, the object moves to the
left (with a negative velocity).
|
|
(b)
|
For φ
= - π/2.
x(t) = xm cos (2 πt/T
- π/2).
By trigonometric identity, cos (C - D) =
cos C cos D + sin C sin D, with C = 2πτ/T
and D = π/2, x(t)
= xm[cos 2πt/T
cos π/2 +
sin 2 πt/T
sin π/2]x(t) = xm[(cos
2πt/T)(0)
+ (sin 2πt/T)(1)] = xm
sin 2 πt/T. Notice the first
maximum in Fig. b lags that in Fig. a by π/2
radians.
|
|
(e)
|
v(t) = -2 π
xm/T sin (2 π
t/T - π/2).
By trigonometric identity, sin (C - D) =
sin C cos D - cos C sin D, v(t) =
-2 π xm/T[(sin
2 πt/T)(0) - (cos2 πt/T)(1)]
v(t)
= (2 π xm/T)
cos 2 πt/T. For φ
= - π /2 and
t = 0, xo = 0 and vo = +2 π
xm/T.
|
|
(c)
|
For φ
= - π, x(t) = xm
) =
xm[cos 2 πt/T
cos π + sin 2 πt/T
sin π] =
xm[(cos 2 πt/T)(-1)
+ (sin 2 πt/T)(0)]
x(t) =
-xm cos 2 πt/T.
Notice that Fig. c lags Fig. a by π radians.
|
|
(f)
|
v(t) = -xm(2 π/T)
sin (2 πt/T - π)
=
-(2 πxm/T)[sin
2 πt/Tcos π
-cos 2 πt/T sin π]
=(-2 πxm/T)[(sin
2 πt/T)(-1) -(cos
2 πt/T)(0)].
v(t) = (2 πxm/T)
sin 2 πt/T. For φ
= π and t = 0, xo
= -xm and vo = 0. Immediately
after t = 0, the object moves to the right with a positive
velocity.
|
|
(g)
|
The usefulness of φ
is to state the initial conditions. Note:φ = + π and - π
give the same result.
|
|
|
|
8.
|
When the object comes to rest, the net
force acting on it is zero. The magnitude of the force due
to the spring equals the gravitational force,
kx = mg, or k = mg/x = 0.50 kg(9.8 m/s2)/0.10 m
= 49 N/m.
|
|
|
9.
|
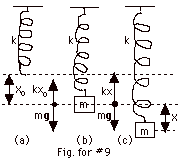
In Fig. for #9a, the spring is not stretched.
In Fig. for #9b, the mass is attached and the spring is stretched
a distance of xo.
(a) The mass comes to rest and Fnet = ma = m(0).
Taking down to be positive,
-kxo + mg = 0 (Equation
1)
(b) In Fig. for #9c, the spring has been displaced an additional
distance x.
Now Fnet = ma, where a ≠ 0 once the spring
is released. Taking the direction of x, which is down, as
positive,
-kx - kxo + mg =
ma (Equation
2)
From Eq. 1, we see that - kxo + mg = 0. Eq. 2 becomes
-kx = ma or a/x = -k/m. The ratio of a to x is the same whether
the spring is mounted horizontally or vertically.
(c) As before, a/x = -(2 π/T)2
= -(2 πf)2
= -k/m and f= (1/2 π)(k/m)1/2.
|
|
|
10.
|
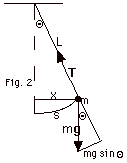
(a) The forces acting on the pendulum bob are itsweight mg
and the tension T in the string.
(b) The only force tangent to the path is a restoring force
-mg sin Θ. From the triangle
with distances, we find that sin Θ= x/L and -mg sin Θ
= -(mg/L)x.
For small displacements, x ≈s and we can think
of the displacement and the restoring force acting horizontally.
(c) Since m, g, and L are constants,
the restoring force, -(mg/L)x, is directly proportional to
the displacement and in the opposite direction. The pendulum
is an example of simple harmonic motion. a/x = -(g/L) = -(2 π/T)2
= -(2 πν
)2.
ν = (1/2 π)(g/L)1/2.
|
|
|
11.
|
| |
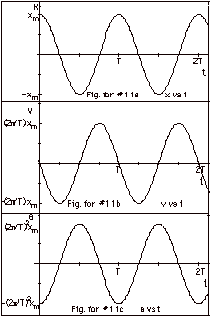 |
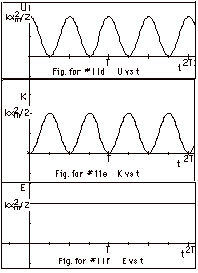 |
|
(a)
|
x(t) = xm cos 2 πt/T
|
|
(b)
|
v(t) = dx/dt = -(2 π/T)xm
sin 2 πtT
|
|
(c)
|
a(t) = dv/dt = - (4 π2/T2)xm
cos 2 πt/T
|
|
(d)
|
U(t) = 1/2 kx2 = 1/2
kxm2 cos22 πt/T
|
|
(e)
|
K(t) =1/2 mv2 = 1/2
(m4 π2/T2)xm2
sin2 2 πt/T
= 1/2 (k)xm2 sin2 2 πt/T,
since k/m = 4 π2/T2.
|
|
(f)
|
E(t) = U(t) + K(t) = 1/2 kxm2(cos2
2 πt/T + sin2
2 πt/T) = 1/2 kxm2
= a constant. U is a maximum twice each period
when x = xm and v = 0.
K is a maximum each period when x = 0 and v =2 πxm/T.
U + K = E = constant.
|
|
|
|
12.
|
E = 1/2 kxm2 =
1/2(10 N/m)(0.050 m)2 = 0.0125 J.
U(x) = 1/2 kx2 = 1/2(10 N/m)(0.010 m)2
= 0.0005 J.
K = 1/2 mv2.
E = U + K
0.0125 J = 0.0005 J + 1/2 (0.60 kg)v2.
v2 = 2/0.60 kg[0.0125 - 0.0005]J
0.04 N-m/kg = 0.04 kg-m2/s2-kg
= 0.04 m2/s2.
v = 0.2 m/s
|
|
|
13.
|
Given x(t) = 0.01 m cos (0.02 π
s-1 t - π/2)
compare
with
x(t)
= xm cos (2 πt/T
+ φ) and
find
(a) the amplitude xm = 0.01 m (b) 2 π/T
= 0.02 π s-1;
(b) period T = 100 s,
(c) the frequency ν =
1/T = 0.01 s-1 and
(d) the initial phase φ
= - π/2.
|
|
|
14.
|
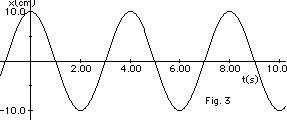
From Fig. 3 above, we see that
(a) the cosine curve repeats itself every 4.0 s so the period
T = 4.0 s, and
(b) the amplitude of the motion xm =10.0 cm.
(c) If we write the equation of motion as a function of the
cosine, we let φ= 0.
x(t) = xm cos 2 πt/T
= 10.0 cm cos 2 πt/4.0
s = 10.0 cm cos πt s-1.
(d) v(t) = dx/dt = -10.0 π/2
cm/s sin πt s-1/2.
|vmax| = 5.0 π
cm/s.
(e) a(t) = dv/dt = -10.0 ( π/2)2cm/s2
cos πt s-1/2.
_ amax_
= 2.5 π2 cm/s.
|
|
|
15.
|
For a total swing back and forth of
4.0 cm, the amplitude xm is 2.0 cm.
For x(t) = xm cos (2 πt/T
+ φ), v(t) = dx/dt
= -xm2 π/T sin
(2πt/T + φ).
The maximum velocity 10 cm/s occurs at the center of the swing
when x = 0. When cos (2 πt/T
+ φ) = 0, sin (2 πt/T
+ φ) = 1 and vmax
= 2πxm/T.
T = 2 πxm/vmax=
2 π(2.0 cm)/10 cm/s = 0.4 π
s.
|
|
|
16.
|
x(t) = 4.0 cm cos ( πt
s-1 - π/6).
2.0 cm = 4.0 cm cos ( πt
s-1 - π/6).
cos ( πt s-1 -
π/6) = 0.5 and ( πt
s-1 - π/6)
= π/3 (or 600).
v(t) = dx/dt = -4.0 π cm/s
sin ( πt s-1 - π/6).
When ( πt s-1 -
π/6) = π/3,
sin π/3 = 0.866,
and
v = -4.0 π(0.866) cm/s = -10.9 cm/s.
|
|
|
17.
|
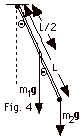
|
(a)
|
τ
= r x F
|
 |
| |
τ
= rF sin _r, F
|
About the pivot point, the torque for
the rod of mass m1 is -(L/2)m1g sin
Θ and for the point mass
it is -Lm2g sinΘ.
The negative signs occur because they are restoring
torques. When the pendulum is swinging counterclockwise, the
torque tends to make it swing clockwise. The moment of inertia
of the rod about an end is 1/3 m1L2.
The moment of inertia of a point particle of mass m2
a distance L from the axis is m2L2.
|
(b)
|
t
= Ia
|
| |
-Lg(m1/2
+ m2)sin Θ
= (m1/3 + m2)L2
d2Θ/dt2
|
| |
For small Θ,
sin Θ
is approximately equal to Θ
so that
|
| |
-Lg(m1/2
+ m2) Θ
= (m1/3 + m2)L2
d2Θ/dt2
|
| |
or
d2Θ/dt2
+ [g(m1/2 + m2)/(m1/3
+ m2)L]Θ
= 0
|
(c) Comparing with d2x/dt2 + [k/m]x
= 0 for which T = 2 π (m/k)1/2,
we find for this pendulum, T = 2 π
[2(m1 + 3m2)L/(m1 + 2m2)3g]1/2
|
|
|
18.
|
|
Fnet = ma = m d2x/dt2
|
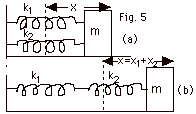 |
(a) For Fig. 5a,
-k1x - k2x = -(k1
+ k2)x = m d2x/dt2, or
d2x/dt2 + [(k1
+ k2)/m]x = 0
Compare with,
d2x/dt2 + [k/m]x = 0, when
ν = (1/2 π)(k/m)1/2
and
find for this case,
ν = (1/2 π)[(k1
+ k2)/m]1/2
The"effective" spring constant for springs in parallel
is
keff= k1 + k2 .
. + kn
(b) For Fig. 5b, the spring with constant k2 is in
contact with mass m that has a displacement x = x1
+ x2, where x1 is the extension of the
spring with constant k1 and x2 the extension
of the spring with constant k2. The force on the
object is,
-k2x2 and -k2x2
= m d2x/dt2 (Equation1)
Also
x = x1 + x2 (Equation
2)
and the magnitude of the force on the second spring due to the
first spring equals the magnitude of force on the first spring
due to the second spring, or
k1x1 = k2x2
or x1 = k2x2/k1 (Equation
3)
Substituting Eq. 3 into Eq. 2,
x = (k2x2/k1)
+ x2 = (k1 + k2)x2/k1
, or
x2 = k1x/(k1 + k2) (Equation
4)
Substituting Eq. 4 into Eq. 1,
-[k2k1/(k1 + k2)]x
= m d2x/dt2 , or
d2x/dt2 + [{k1k2/(k1
+ k2}/m)]x = 0
Comparing with,
d2x/dt2 + [k/m]x = 0
For this case,
ν = (1/2_)[{k1k2/(k1
+ k2)}/m]1/2
The"effective" spring constant for series is,
keff = {k1k2/(k1
+ k2}, or
1/keff = 1/k1 + 1/k2 + .
.+ 1/kn.
|
|
|
19.
|
Imagine the spring cut into thirds with
each part having a spring constant k’.
When the three springs are connected in series, the spring constant
is
k = 10.0 N/m. For series,
1/k = 1/10 N/m = 1/k’ + 1/k’ + 1/k’=
3/k’
k’ = 3k = 30.0 N/m
When two of these springs with k’ are connected in series,
1/k” = 1/k’ + 1/k’ = 2/30 N/m
or the spring constant with 2/3 of the spring left (1/3 cut
off) is
k” = 15 N/m
T = 2 π(m/k”)12
= 2 π(0.30/15)1/2 s
= 0.89 s.
|
|
|
20.
|
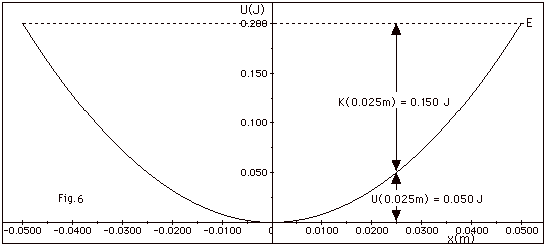
|
|
|
|
(a) From Fig. 6 above, at x = 0.025 m,
U = 0.050 J.
(b) E = 0.200 J = U + K = 0.050 J + K. K = 0.150
J.
(c) U = 0.050 J = 1/2 kx2= 1/2 k(0.025 m)2, or
k = 0.10 J/6.25 x 10-4
m2 = 160 N/m.
(d) K = 0.150 J = 1/2 mv2 = 1/2(0.30kg)v2,
or
v2 = 2(0.150)/0.30
m2/s2 = 1.0 m2/s2
or v = 1.0 m/s.
(e) E = 0.200 J =1/2 kxm2 =1/2 (160
N/m)xm2, or
xm = (25 x 10-4)1/2m
= 0.05m.
(f) v is a maximum when the potential energy is a minimum.
This occurs for x = 0 and, therefore, U = 0 with K = E = 0.200
J = 1/2 mvmax2 = 1/2(0.30kg)vmax2.
vmax = 1.15 m/s.
|
|
|