|
Answers - Work and Energy
|
|
|
1.
|
|
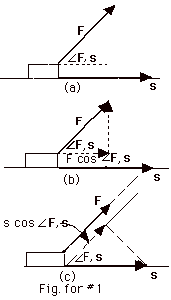
Work equals the force F times the
displacement s times the cosine of the angle  F,s
between the force F and the displacement s: F,s
between the force F and the displacement s:
W = (Fs cos  F,s) F,s)
If we rewrite work as W = (F cos  F,s)s, F,s)s,
we see from Fig. 1b that we may say, alternatively,
that work is the component of the force, F cos  F,s,
in the direction of the displacement times the displacement. F,s,
in the direction of the displacement times the displacement.
From Fig. 1c we find we may also write
W = F (s cos  F,s)
or work is the product of the force and the component
of the displacement, (s cos F,s)
or work is the product of the force and the component
of the displacement, (s cos  F,s),
in the direction of the force. F,s),
in the direction of the force.
|
|
 |
|
|
|
2.
|
In general, W = (Fs cos  F,s) F,s)
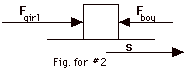
(a) For the girl, W = 18 N(4 m)(cos 00) = 18 N(4
m)(1) = 72 J.
(b) For the boy, W = 12 N(4 m)(cos 1800) = 12 N(4
m)(-1) = -48 J.
(c) You can find the work done by the net force in two ways:
- Since work is a scalar quantity, add the work done by
each algebraically, that is, 72 J - 48 J = 24 J.
- First find the net force. Taking to the right to be positive,
Fnet = 18 N - 12 N = 6 N to the right.  Fnet,
s = 00. Fnet,
s = 00.
Work done by net force = 6 N(4 m) cos 00 = 6
N(4 m)(1) = 24 J.
|
|
|
3.
|

If you do not raise the object or increase its velocity, there
is no increase in the object's potential energy or in its
kinetic energy. The physicists' definition of work demands
that when you do work on an object its energy increases. For
the situation in Fig. 1, you are exerting a force through
a distance, but you do no work. For this reason, we define
work W as the force F times the displacement s times the angle
between F and s or  F,s.
In Fig. 1, F,s.
In Fig. 1,  F,s
= 900 and cos 900 = 0. With this
definition of work, we correctly predict that no work is done
moving an object horizontally without increasing its speed.
You may tire while moving the object because your tensed muscles
are continually contracting and relaxing in minute movements.
You, however, have done no work on the object as defined in
a physical sense. F,s
= 900 and cos 900 = 0. With this
definition of work, we correctly predict that no work is done
moving an object horizontally without increasing its speed.
You may tire while moving the object because your tensed muscles
are continually contracting and relaxing in minute movements.
You, however, have done no work on the object as defined in
a physical sense.
|
|
|
4.
|
The force that produces a centripetal
acceleration is always in toward the center or perpendicular
to the path. The angle between the tension and the displacement
is 900. Since cos 900 = 0, no work is
done by the tension in the string. Also note that the potential
energy and the kinetic energy of the object do not change.
|
|
|
5.
|
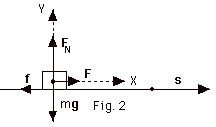
(a) The angle between F and s is 0o.
The work done by F = Fs cos
0o = 12 N(4 m)(1) = 48 J.
(b) The angle between FN and s is
90o.
The work done by FN
= FNs cos 90o = FNs(0) =
0.
(c) The angle between mg and s is -90o.
The work done by mg = mgs cos
-90o = mgs(0) = 0.
(d) To find the frictional force f, notice that
(Fnet)y = may = m(0) = 0.
FN - mg = 0 and
FN = mg.
f = µkFN
= 0.50(mg) = 0.50(20 N) = 10 N.
The angle between f and
s is 180o.
The work done by f = fs cos 180o
= 10 N(4 m)(-1) = - 40 J.
(e) The work done by the net force = 48 J - 40 J = 8 J, or
(Fnet)x = 12
N - 10 N = 2 N.
Work done by net force = 2 N(4 m)cos
00 = 8 J.
|
|
|
6.
|
For the raindrop to fall with a constant
speed, the net force acting on the drop must equal 0. Thus
mg - f = 0 or mg = f, where f is the frictional force of the
air on the drop and I have taken down as positive.
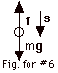
Work = Force (displacement)  F,s.
The gravitational force mg is in the same direction
as the displacement s. Work by gravitational force
= mgs cos 00 = F,s.
The gravitational force mg is in the same direction
as the displacement s. Work by gravitational force
= mgs cos 00 =
mgs(1) = 3.35 x 10-5 kg(10 m/s2)(100
m)(1) = 3.35 x 10-2 J. The frictional force of
the air is opposite to the direction of the displacement s.
Work by frictional force of air = fs cos 1800 =
-3.35 x 10-2 J.
|
|
|
7.
|
Kinetic energy K = 1/2 mv2
= 1/2(52 kg)(14.0 m/s)2 = 51 x 102 J.
|
|
|
8.
|
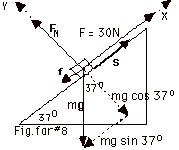
(a) In the figure, we take the Y-axis
perpendicular to the incline.
|
(Fnet)y
= may
|
 |
|
FN - mg cos 370
= m(0)
|
|
FN = mg cos 370
= (2.0 kg)(10 m/s2)(0.8) =16N
|
|
f = µkFN =
0.50(16 N) = 8.0 N
|
(b) Work done by F = Fs cos  F,s
= 30N(4m)(cos 00) = 30 N(4.0 m)(1) =120 J. F,s
= 30N(4m)(cos 00) = 30 N(4.0 m)(1) =120 J.
(c) Work done by FN = FNs cos 900
= FNs(0) = 0.
(d) Angle between mg and s = -(90 + 37)0.
Work done by mg = mgs cos  mg,s
= 2.0 kg(10 m/s2)(4.0 m)cos {-1270)}
= 2.0 kg(10 m/s2)(4.0 m) (-0.6) = -48 J. mg,s
= 2.0 kg(10 m/s2)(4.0 m)cos {-1270)}
= 2.0 kg(10 m/s2)(4.0 m) (-0.6) = -48 J.
(e) Work done by friction = f(s)cos 1800 = 8.0
N(4.0 m)(-1) = -32 J.
(f) Work by net force =120 J - 32 J + 0 - 48 J = 40 J.
(g) By work-energy theorem, work done by net force = 40 J
= ΔK
= 1/2 mvf2 - 1/2 mvi2
= 1/2(2kg)vf2 - 0.
40 J = 40 N-m = 40 (kg-m/s2)-m
= 40 kg-m2/s2 = (kg)vf2.
vf = √40
m/s = 2√10 m/s.
|
|
|
9.
|
| (a) |
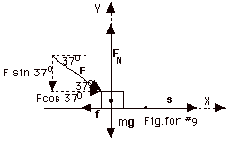
For the Y-axis, (Fnet)y
= may
|
 |
| |
From the figure,
|
| |
FN - F sin 370
- mg = 0
|
| |
FN = F sin 370
+ mg
|
| |
FN = (30 N)(0.6) +
20 N = 38 N
|
| |
f = µkFN =
(0.50)(38 N) = 19 N
|
(b) Work by f = fs cos  f,
s = (19 N)(4.0 m)(cos 180o) = -76 J f,
s = (19 N)(4.0 m)(cos 180o) = -76 J
(c) Work done by F = Fs cos  F,s
= 30 N(4.0 m)(cos 37o) =120 J(0.8) = 96 J F,s
= 30 N(4.0 m)(cos 37o) =120 J(0.8) = 96 J
(d) Work done by FN = FNs
cos  FN,s = FNs cos 90o
= FNs (0) = 0
FN,s = FNs cos 90o
= FNs (0) = 0
(e) Work done by mg = mgs cos  mg,
s = mgs cos (-90o) = mgs (0) = 0 mg,
s = mgs cos (-90o) = mgs (0) = 0
(f) Net work done = Work by f + Work by
F + Work by FN + Work by mg
= -76 J + 96
J + 0
+ 0
= 20 J
(g) By work energy theorem,
Work done by net force = Δ
kinetic energy = Kf - Ki = 1/2 mvf2
- 1/2 mvi2
20 J = 1/2 (2 kg)vf2 - 0
vf = (20 J/kg)1/2 = (20 N-m/kg)1/2
= {20 (kg-m/s2)(m/kg)}1/2 = √20
m/s
= 2√5 m/s.
|
|
|
10.
|
Work = force (displacement) cos  F,s. F,s.
(a) The angle between the force exerted by the person and
the displacement is 00. Work by person =10
N(1.0 m) = 10 J.
(b) The gravitational force = mg = 1.0 kg(10 m/s2)
= 10 N. To lift the object with a constant velocity the force
of the person must be equal in magnitude to the gravitational
force. The angle between mg and s is 1800.
Work done by gravity = 10 N(1.0 m)cos 1800 = -10
J.
(c) Increase in potential energy = mgh, where h is the height
to which the object is raised = 10 J. The increase in the
potential energy equals the work done by the person in raising
the object with a constant velocity or it equals the negative
of the work done by the gravitational force.
(d) The increase in kinetic energy is zero because the work
done by the net force equals zero.
|
|
|
11.
|
(a) Now work done by person = 12 N(1.0
m) = 12 J.
(b) Work done by gravitational force still equals -10 J.
(c) Increase in potential energy equals the negative of the
work done by the gravitational force = 10 J.
(d) Work done by the net force = 12 J - 10 J = 2 J = increase
in kinetic energy.
|
|
|
12.
|
(a) Work done by friction = fs cos 180o
= 72 N(3.0 m)(-1) = -216 J.
(b) Work by net force = work done by friction = change in
kinetic energy
-216 J = 1/2 (12 kg)v23.0m - 1/2(12
kg)(10 m/s)2
-216 J + 600 J= 1/2(12 kg)v23.0m.
V3.0m = 8.0 m/s.
(c) Work done by friction = 72 N(s)(-1) = change in kinetic
energy
= 0 - 600 J. s = 8.3 m
|
|
|
13.
|
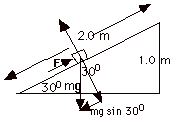
(a) For the figure below, sine of the
angle of incline = 1.0/2.0. Angle of incline = 300.
For motion up the plane with constant velocity, the net force
in that direction must be zero.
|
Fnet up the plane =
ma = m(0)
|
 |
|
F - mg sin 300 = 0
|
|
Force of person = F = mg
sin 300
|
|
= 2.0 kg(10 m/s2)(1/2)
= 10 N.
|
The angle between the force of the person
and the displacement is 00. Work done by person
in moving the object up the plane of 2.0 m with a constant
velocity = 10 N(2.0 m)(cos 00) = 10 N(2.0 m)(1)=
20 J.
(b) The component of the force of gravity down the plane is
mg sin 300 = 10 N. The angle between this component
and the displacement up the incline is 1800. The
work done by the gravitational force = (10 N)(2.0 m)(-1) =
-20 J. The work done by the net force = work done by person
+ work done by gravitational force = increase in kinetic energy.
Work done by person =
increase in kinetic energy - work done by gravitational
force =
{1/2 (2.0 kg)(3.0 m/s)2 - 0} - (-20 J) = 29 J.
(c) Again,
Fnet up the plane = ma = m(0) = 0,
but now there is a frictional force of 3.0 N, so
F - mg sin 300 - 3.0 N = 0 or F = 13 N.
Work done by person = 13 N(2.0 m)(1) = 26 J.
|
|
|
14.
|
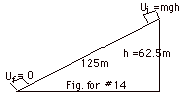
Take Uf at the bottom of the incline = 0.
Work by friction = fs cos 180o =(Uf
+ Kf) - (Ui + Ki).
f(125 m)(-1) = {0 +(1/2)(1.0 kg)(25 m/s)2} - {1.0
kg)(10 m/s2)(62.5 m) + 0}
-125 m f = 312.5
J - 625 J = -312.5 J. f = 2.5 N
|
|
|
15.
|
The total energy E = U + K or K = E -
U
= {-21.7 - (-43.4)}10-19 J. K = 21.7
x 10-19 J.
While the total and potential energy are negative, classically
the kinetic energy must always be positive.
|
|
|
16.
|
(a) acceleration a = Δv/ Δt
= (0.20 - 0)m/s/0.50 s = 0.40 m/s2.
F = ma = 2000 kg(0.40 m/s2)
= 800 N.
(b) K = 1/2(2000 kg)(0.20 m/s)2 = 40 J.
(c) Work done by net force = change in kinetic energy = 40
J.
(d) Work = Fs = 800 N s = 40 J. s
= 40 J/800 N = 0.05 m.
|
|
|
17.
|
(a) i . i =
(1)(1) cos 00 = 1
(b) i . j = j . i
= (1)(1) cos 900 = 0
(c) j . j = (1)(1) cos 00
= 1
(d) W = F . s = 20 N j .
4 m i = 80 J(j . i) = 0
(e) W = F . s = (3i +
4j)N . (2i - 2j)m =
6J(i . i) - 6J(i . j)
+ 8J(j . i) - 8J(j . j)
= 6 J - 0 + 0 - 8 J = -2 J
|
|
|
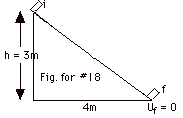
18.
|
Since the incline is frictionless and
no other nonconservative force acts on the object, energy
is conserved. Take the initial point i at the top of the incline
and the final point f at the bottom of the incline. Let Uf
= 0. At the initial point the potential energy is mgh,
where h is the vertical height above the bottom of
the incline. The object being released from the top of the
incline means that its initial velocity vi is
zero so that Ki = 1/2 mvi2
= 0.
From conservation of energy,
| |
|
|
|
|
|
|
 |
|
Ui
|
+
|
Ki
|
=
|
Uf
|
+
|
Kf
|
|
2.0 kg(10 m/s2)(3
m)
|
+
|
0
|
=
|
0
|
+
|
1/2(2.0 kg) vf2
|
| |
|
60m2/s2
|
=
|
vf2
|
|
|
|
or
vf = (60)1/2
m/s = 7.7 m/s
|
|
|
|
19.
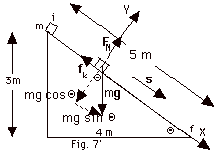
|
At the bottom of the incline Uf
= 0; at top of incline Ui = mgh. Ki
still = 0.
With the frictional force, a nonconservative force acting on
the block, mechanical energy is not conserved.
(Fnet)y = may = m(0).
FN = mg cos Θ;
fk = µkFN = µk
mg cos Θ = µk
mg(4/5).
Since the distance down the plane s = 5 m and cos  fk,s
= 180o: fk,s
= 180o:
|
the work by friction = (fk)
s cos  fk,
s fk,
s
|
 |
|
=µk mg cos
Θ}s cos 180o
|
|
=(1/4)(2 kg)(10 m/s2)(4/5)}(5m)(-1)
= -20 J.
|
|
Work by friction = (Uf
+ Kf) - (Ui + Ki)
|
|
-20
J = (0 + 1/2 mvf’2) - (mgh
+ 0)
|
| |
| |
| |
|
-20 J = 1/2(2 kg)vf’2 -
(2 kg)(10 m/s2)(3 m) = 1kg vf’2
- 60 J
|
|
40 J = 40 N-m = 40 kg m2/s2
= vf’2 kg; vf’
= (40)1/2 m/s = 6.3 m/s
|
|
|
|
20.
|
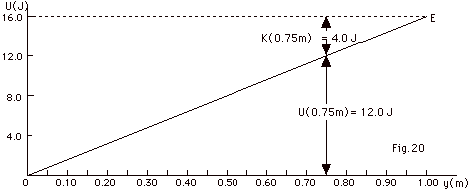
(a) From Fig. for #20, at y = 0.750 m,
U = 12.0 J.
(b) At all times, E = 16.0 J = U + K = U(0.750m) + K(0.750
m)
= 12.0 J + K(0.750 m) or K(0.750m) = 4.0 J.
(c) U = mgh or at 0.750 m, 12.0 J = m(10 m/s2)(0.75
m) or m = 1.6 kg.
(d) K = 1/2 mv2 = 1/2(1.6kg)v2 = 4.0
J or v = √ 5 m/s.
|
|
|
21.
|
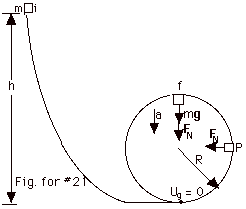
(a) We use conservation of energy to solve the problem. We
take the gravitational potential energy equal to 0 at the
bottom of the loop-the-loop (Fig. for #21). The block is released
at the initial position i so the kinetic energy there is zero.
The block will make it around the loop-the-loop if it can
stay on the loop as it gets to the top of the loop. For this
reason we take the top of the loop as the final position f.
|
Ui
+ Ki = Uf + Kf
|
|
mgh + 0 = 2mgR + 1/2 mvf2
(Equation
1)
|
At the top, the acceleration is in toward
the center.
|
Fnet
= ma, or
|
|
mg + FN = mvf2/R
|
For the minimum height h, we want the
minimum velocity vf, so we set the normal force
FN = 0. Then mg = mvf2/R
or:
Substituting Eq. 2 into Eq. 1: mgh = 5/2
mgR or h = 5R/2.
(b) At P, the potential energy = mgR.
|
Ui
+ Ki = UP + KP, or
|
|
mg(5/2 R) + 0 = mgR + 1/2 mvP2,
or
|
|
mg(3/2)R
=1/2 mvP2, or
|
|
mvP2 =
3mgR
|
At P, the normal force produces the centripetal
acceleration into the center of the circle. At P, mg
is down.
|
Fnet = ma,
|
|
FN
= mvP2/R = {3mgR}/R = 3mg
|
|
|
|
22.
|
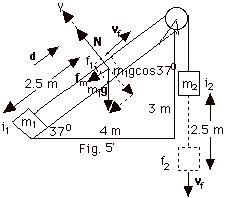
We choose different potential energy positions for the potential
energy equal to zero for m1 and m2.
Notice that when m2 moves down, m1 moves
up the incline. Since we always take the lowest position for
the zero of potential energy, the position of m1
in Fig. 5 (in the statement of the problem) is its lowest
position and we take the potential energy of m1
equal to zero there. The position of m2 in Fig.
5 is its highest position. We take its zero potential at a
point 2.5 m below where it is in Fig. 5, or its dashed position
in Fig. 5'.
|
(Fnet)y =
m1ay
|
|
FN - m1g
cos 370 = m1(0) = 0, or
|
|
FN = m1g
cos 370 = m1g(4/5)
|
|
f = µFN = 0.55(mg)(4/5)
|
|
= 0.55(2.0 kg)(10
m/s2)(4/5)
|
|
= 8.8 N
|
The work done by friction = f(d) cos
 f,d f,d
|
= fd cos 1800
|
|
= -fd
|
|
= -8.8 N(2.5 m)
|
|
= -22 J.
|
In the final position f2,
the potential energy (U2)f of m2
is zero, but in the final position f1, the potential
energy for m1 is m1gh1, where
h1 = the vertical height above the initial position.
Since it goes up the plane 2.5 m and the plane is inclined
at 370, the vertical height h1 = 2.5
m sin 370 = 2.5 m (3/5) = 1.5 m.
(U1)f = (m1g)h1 =
(20 N)1.5 m = 30 J. For the system Uf = (U1)f
+ (U2)f = 30 J + 0 = 30 J. Since both
blocks move together, their final speed vf is the
same. The final kinetic energy of the system Kf
= (1/2)(m1 + m2)vf2
= 1/2(6.0 kg) vf2. The initial
potential energy (U1)i of m1
at i1 is zero. The initial potential energy of
m2 at i2 is (U2)i =
m2g(2.5 m) = (4.0 kg)(10 m/s2)(2.5 m)
= 100 J. For the system, Ui = 100 J. Both blocks
were initially at rest. For the system Ki = 0.
Again,
| Work by friction |
=
|
{ Uf + Kf
}
|
-
|
{ Ui + Ki
}
|
|
-22 J
|
=
|
{30 J + 3.0 kg(vf2)}
|
-
|
{100 J + 0}
|
|
-22 J - 30 J + 100 J = 48 J = 48
N-m = 48 kg-m2/s2 = 3.0 kg vf2,
or
|
|
vf2 =16 m2/s2
|
|
and
vf = 4 m/s.
|
|
|
|
23.
|
(a) Take UB = 0 and use conservation
of energy:
| |
|
|
|
|
|
|
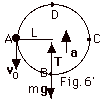 |
|
UA |
+
|
KA
|
=
|
UD
|
+
|
KD
|
|
mgL
|
+
|
1/2(m)vo2
|
=
|
mg2L
|
+
|
0 |
|
or
1/2(m)v02 = mgL or vo
= (2gL)1/2
|
| |
|
|
|
|
|
|
Note: If the ball were attached to a string, it could not go
up to D and stop. A string can only pull in toward the center
of a circle so at the top of the circle, the gravitational force
would cause the ball to fall down. On the other hand, a rod
can provide a force up or down, so when it comes to rest, the
upward force of the rod balances the gravitational force and
the ball returns on its path clockwise.
(b) At B (Fig. 6' above) the acceleration is up so take up as
positive.
|
Fnet = ma
|
|
T - mg = mvB2/L
(Equation
1)
|
Turn to conservation of energy to find vB:
|
UA
|
+ |
KA
|
= |
UB
|
+ |
KB
|
|
mgL
|
+ |
1/2(m)vo2
|
= |
0
|
+ |
(1/2)mvB2
|
From (a), mgL + (1/2)m{(2gL)1/2}2
= 0 + (1/2)mvB2
or
mgL + mgL = (1/2)mvB2
or
mvB2 = 4mgL (Equation
2)
Substituting Eq. 2 into Eq. 1: T - mg = 4mgL/L = 4mg and
T = 5mg
| (c) Work
done by frictional force |
= |
(UC + KC) |
- |
(UA
+ KA) |
| |
= |
(mgL + 0) |
- |
(mgL + mgL) |
| |
= |
mgL |
- |
2mgL
= -mgL |
(d) Work done by frictional force = (UB
+ KB) - (UA + KA)
|
=
|
(0 + 0)
|
-
|
(mgL + mgL) = -2mgL
|
|
|