Review - Induction

1.

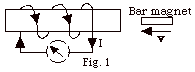
A magnet moves toward a coil of wire and the current is induced in the sense shown in Fig. 1 below. Is the pole of the magnet closes to the coil acting as a north-seeking or south-seeking pole?

2.

A bar magnet drops through a conducting loop. Will the acceleration of the bar magnet be constant? Explain your answer.

3.

A square loop of wire, 2.0 meters on a side, has a resistance of 0.04 ohms. The loop is in a horizontal plane. Initially, a magnetic field B = 0.080 N/A-m points vertically downward into the loop. If this field is reduced in magnitude to 0.040 N/A-m at a constant rate in 2.0 s, find the direction and magnitude of the induced current.

4.

A loop of wire acde in Fig. 2 below moves to the right in the magnetic field of a very long current-carrying wire. Is there an induced current in the loop for Fig. 2a and Fig. 2b? If there is an induced current, what is its direction?

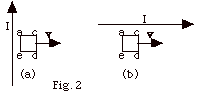
5.

A circular metal chain in a horizontal plane is in a vertical magnetic field upward. The chain has a resistance of 0.001 Ω and its length is 0.40 π m. (a) If the magnetic field increases from 0.010 N/A-m to 0.060 N/A-m in half a second, find the current that is produced in the coil. (b) Draw a diagram of the chain and field, and indicate the direction of the current in the chain. (c) Does the chain tend to expand or contract while the magnetic field increases? (d) When the field becomes steady at 0.060 N/A-m, the chain is withdrawn in 0.30 s. What average current is produced while the chain is withdrawn? Draw a diagram indicating the direction of the induced current. Does the magnetic force on the chain hinder or aid the withdrawal of the chain from the field?

6.

A loop of wire rotates with a constant angular velocity ω in a constant horizontal magnetic field B. At any instant, the angle between the magnetic field and the normal N to the surface of the loop is Θ = ωt. Write an expression for (a) the magnetic flux through the coil and (b) the emf induced in the coil at any instant. What is the value of Θ when (c) the magnetic flux and (d) the emf is a maximum?

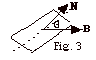
7.

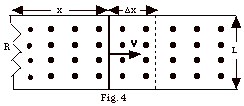
Figure 4 below shows a conducting rod of length L being pulled along horizontal, frictionless, conducting rails at a constant velocity v. A uniform vertical magnetic field B out of the page fills the region in which the rod moves. Find (a) the magnetic flux when the rod is a distance x from the left end of the conducting rails, (b) the change in magnetic flux when the rod moves to the right a distance Δx, (c) the induced emf ε, (d) the direction of the induced current, (e) the induced current in the loop of total resistance R, (f) the power dissipated in the resistance R in terms of B, L, v, and R, (g) the force that must be applied by an external agent to maintain the motion, (h) the power supplied by the external agent, and (i) a comparison of the answers to (f) and (h).

8.

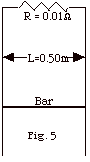
A bar of mass m = 0.50 kg slides downward along stationary wires that are separated by a distance L = 0.5 m and are joined at the top by a resistance R = 0.010 Ω (Fig. 5 below). A uniform magnetic field B = 0.20 N/A-m points into the paper. (a) If the bar slides down, what is the sense of the current through it? (b) At what speed v will the bar experience no force?

9.

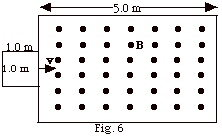
A square loop of wire 1 m on a side moves with a speed v = 0.5 m/s into a region of a magnetic field B = 1.0 T out of the page, as shown in Fig. 6 below. At t = 0, the loop of wire is just about to enter the magnetic field. (a) Plot the magnetic flux through the loop of wire as a function of time at 1-s intervals for 12 s. (b) Now plot the induced emf in the coil for the same time and interval of time. (c) If the coil has a resistance R = 0.01 Ω find the induced current in the coil at the various times. Describe the sense of the current as the coil passes through and out of the field.

10.

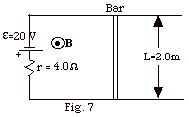
A conducting bar rests across horizontal tracks that are connected on the left by a battery of emf = 20 V and internal resistance r = 4 ohms (Fig. 7 below). The tracks are separated by a distance L = 2.0 m. A magnetic field B = 0.10 N/A-m points vertically upward. If the magnetic field is increased to 1.10 N/A-m at a uniform rate over a period of 0.10 s, how far from the left end of the rails must the bar be placed at rest in order to experience no net force?

11.

In Problem 10, if B remains constant at 1.10 N/A-m, at what constant velocity v (magnitude and direction) will the bar experience no net force?

12.

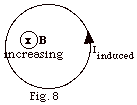
In Fig. 8 below, a circular wire encloses a magnetic field into the page that is increasing. There is an induced current in the wire counterclockwise to oppose the change that produced it. Can you think of this as changing magnetic flux producing an electric field, which, in turn, produces a current? If so what is the direction of the electric field. Would, then, a changing magnetic field produce an electric field, even if a circular wire were not in this space?

13.

A positively charged particle moves in a circle of radius R in the plane of the page with velocity v when a magnetic field B is into the page. (a) If the magnetic field is increased, will the speed of the charged particle remain the same increase, or decrease? (b) Will your answer be the same if the magnetic field is out of the page and increasing? (c) If it is out of the page and decreasing? (d) If the particle is negatively charged and the magnetic field is into the page and increasing? Explain your answers.

14.

A rod with length L, mass m and resistance R slides without friction down two parallel conducting rails inclined at an angle Θ with the horizontal. The rails and the bar that connects them at the bottom of the incline have negligible resistance. Find the constant velocity v achieved by the wire in a uniform magnetic field B directed vertically upward.