|
Review - Potential Energy, Potential,
and Capacitors
|
|
|
1.
|
Determine the electric potential due to two point charges,
Q1 and Q2, along a perpendicular
bisector at point P of the line joining the charges (Fig.
1 below). (b) What is the potential at P when r >> a?
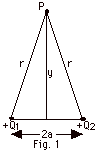
|
|
|
2.
|
Find (a) the electric potential at point P in Fig. 2 below.
(b) Find the work done in bringing up a charge of +3 nC from
infinity. (c) Repeat (a) and (b) for
q2 = +1 nC.
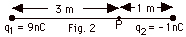
|
|
|
3.
|
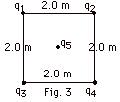
In Fig. 3 below, q1 = q2 = -200µC,
q3 = q4 = +100mC and the charge at the
center of the square q5 = +20µC. With
q5 removed in Fig. 3, find (a) the potential at
the center of the square and (b) the work done to bring q5
from infinity to the center of the square.
|
|
|
4.
|
A charged particle with q = +10-6 C and mass
m = 10-3 kg is placed between the plates of a parallel
plate capacitor and is at rest. (a) Draw the capacitor with
charges, label the forces acting on the particle, and calculate
the electric field between the plates. (b) Given the distance
between the plates as
10-3 m, find the potential difference across
the plates.
|
|
|
5.
|
An alpha particle (charge +2e) approaches a gold nucleus
(charge +79e) from a very great distance, starting with kinetic
energy K. The alpha particle just touches the surface of the
nucleus (the radius of the gold nucleus is
7.0 x 10-15 m) where its velocity is reversed.
Find the initial kinetic energy of the alpha particle.
|
|
|
6.
|
A proton of mass m = 1.67 x 10-27
kg and charge q = e = 1.60 x 10-19 C is accelerated
from rest through a potential difference of 100 V. What
velocity does it achieve?
|
|
|
7.
|
(a) What is the potential energy of a
system of a charge -q at a distance r from a charge +Q? (b)
How much work is required to move a charge -q around a circular
path which has +Q at the center of the circle?
|
|
|
8.
|
A proton of charge +e gains an energy
of 4.8 x 10-19 J when it is accelerated through
a potential difference Vab. (a) What is Vab?
(b) An alpha particle of charge +2e is accelerated through
the same potential difference. How much energy does it acquire?
|
|
|
9.
|
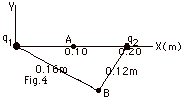
A point charge q1 = +80 nC
is situated on the X-axis at the origin and a second point
charge q2 = -60 nC is placed at x = +0.20 m, as
shown in the figure below. The field point A is located on
the x-axis at x = 0.10 m. A second field point B is
in the X-Y plane at a distance of 0.16 m from q1
and 0.12 m from q2. Find (a) the potential at point
A, (b) the potential at point B, and (c) the work done
in transferring a charge of +10 µC from B to A.
|
|
|
10.
|
A constant electric field E = 104
N/C exists between two parallel plates which are separated
by 0.10 m. (a) How much work is done to carry a charge of
+10-6 C from the negative plate to the positive
plate without increasing its kinetic energy? (b) What is the
potential energy difference between the plates? (c) What is
the potential difference between the plates?
|
|
|
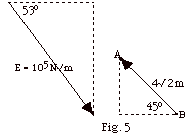
11.
|
A particle of charge q = 10-6
C is placed in an electric field E = 105 N/C directed
at an angle of 53o below the horizontal (Fig. 5
below). (a) How much work is done to carry the charge
from B to A in Fig. 5 without increasing its kinetic energy?
(b) What is the potential energy difference UA -
UB? (c) What is the potential difference
VAB?
|
|
|
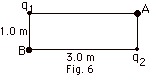
12.
|
In Fig. 6 below, q1 = -4 µC
and q2 = +2 µC. Find (a) the potential at
B, (b) the potential at A, (c) the work done to move
a particle with q3 = +3 µC at a constant speed
from B to A. (d) Does the work done depend on the path from
B to A?
|
|
|
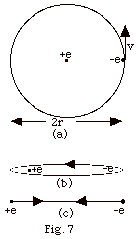
13.
|
Assume that an electron of mass m moves
in a circle of radius r with a constant speed around a stationary
proton (Fig. 7a below). (a) What is the electric potential
energy of this system in terms of k, e, and
r? (b) The electric force of the proton on the electron
provides the centripetal acceleration. Use Newton's second
law of motion to find mv2. Find (c) the total
energy and the angular momentum of the system.
|
|
|
14.
|
In one model of the hydrogen atom, the
electron moves in an elliptical orbit around a stationary
proton. For the very "skinny" ellipse of Fig. 7b
above, the electron's motion can be approximated by motion
back and forth along a straight line (Fig. 7c above). Find
(a) the electric potential energy of the system when the electron
is a distance 2r from the proton and (b) the kinetic energy
of the system when the electron is at this distance. (c) Compare
the total energy and the angular momentum of the system with
the model of Problem 13.
|
|
|
15.
|
Each of three parallel plate capacitors
has area A and spacing d. Find the spacing d’ of a single
capacitor of plate area A if its capacitance equals that of
the three connected in (a) parallel (b) series.
|
|
|
16.
|
A spherical capacitor of radius R1
is charged to a potential difference of (Vab)i.
The charging battery is then disconnected and the capacitor
is connected in parallel with a second (initially uncharged)
spherical capacitor of radius R2. The measured
potential difference drops to (Vab)f.
Find R2 in terms of R1, (Vab)i,
and (Vab)f.
|
|
|
17.
|
A parallel plate capacitor has a capacitance
C when the plates have an area A, a plate separation d and
the plates are in a vacuum. The charge on the plates is Q
when a battery of potential difference of Vab is
placed and kept across the capacitor. Find what happens to
(i) the capacitance, (ii) charge and (iii) the electric field
when (only one at a time), (a) the plate separation is doubled
and (b) a dielectric of constant κ
= 2 is inserted between the plates.
|
|
|
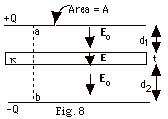
18.
|
Determine the capacitance of a parallel
plate capacitor in which the region between the plates is
partially filled with a dielectric slab of thickness t and
dielectric constant κ,
as shown in the Fig. 8 below.
|
|
|
19.
|
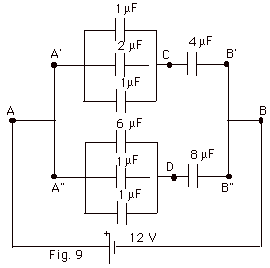
Find the equivalent capacitance of the
circuit in Fig. 9 below and the charge on each capacitor.
|
|
|
20.
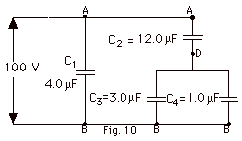
|
Find (a) the equivalent capacitance of
the combination of capacitors shown in Fig. 10 below,
(b) the charge on each capacitor, and (c) the potential difference
VAD and VDB. (d) How much energy is
stored in the capacitors?
|
|