Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 106

Answers - Circuits

1.
  1. The average current density is
    J = I/A = 20A/ π(1.63 x 10-3 m)2 = 2.4 x 106 A/m2.

  2. vd = J/en = 2.4 x 106 A/m2/(1.6 x 10-19C)(8.47 x 1028 m-3) =
    1.8 x 10-4 m/s.

  3. E = ρJ = (1.56 x 10-8 V-m/A)(2.4 x 106 A/m2) = 0.037 V/m.

2.



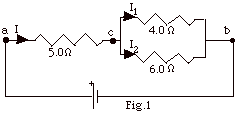
If the current  I1 = 3.0 A in the 4.0 Ω resistor,

Vcb = I1 (4.0 Ω) = 3.0 A(4.0 Ω) = 12 V.
I2 = Vcb/6.0 Ω = 12 V/6.0 Ω = 2.0 A.
I = I1 + I2 = 3.0 A + 2.0 A = 5.0 A.
Vac = IRac = (5.0 A)(5.0 Ω) = 25 V.
Vab = Vac + Vcb = 25 V + 12 V = 37 V.

3.
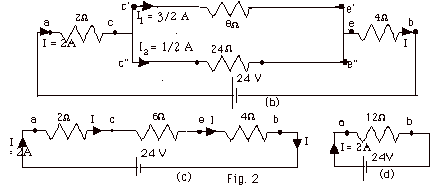
  1. 2 Ω is in series with 6 Ω.  Rc’e’ = (2 + 6) Ω = 8 Ω.

  2. 3 Ω is in series with the 21 Ω.  Rc”e” = (3 + 21) Ω = 24 Ω.

  3. Rc’e’ is in parallel with Rc”e”.
    1/Rce = (1/8 + 1/24)Ω-1 = (3/24 + 1/24) Ω-1.   Rce = 6 Ω.

  4. Rab = Rac + Rce + Reb = (2 + 6 + 4) Ω = 12 Ω.

  5. I = Vab/Rab = 24 V/12 Ω = 2 A.

  6. Vce = IRce = 2A(6 Ω) = 12 V = Vc’e’ = Vc”e”.

  7. I1 = Vc’e’/Rc’e’ = 12 V/ 8 Ω = 3/2 A.

  8. I2 = Vc”e”/Rc”e” = 12 V/24 Ω = 1/2 A.   Note that I1 + I2 = I.

4.


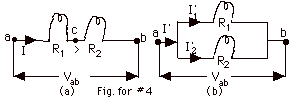
For the resistors in series, the current in each is the same and the power
P = I2R.  Since  R1 > R2,  P1 > P2.

When the resistors are in parallel, the current is not the same in each, but the potential difference across each is the same.
P1 = (I1’) Vab = (Vab/R1)(Vab) = Vab2/R1.
P2 = (I2’) Vab = (Vab/R2)(Vab) = Vab2/R2.
Since  R1 > R2,  now  P2 > P1.


5.


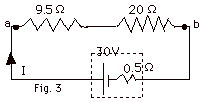
  1. The total resistance of the circuit is (9.5 + 20 + 0.5)Ω = 30 Ω.
    The current  I = 30 V/30 Ω= 1 A.

  2. Power dissipated in external resistances =
    I2(9.5 + 20)Ω = 1 A2 (29.5 V/A) = 29.5 W.
    Power dissipated in the internal resistance =
    I2(0.5 Ω) = (1 A2) (0.5 V/A) = 0.5 W.
    Total power dissipated in resistances =
    (29.5 + 0.5) W = 30 W.

  3. Power supplied when chemical energy is changed into electrical energy = (Emf)(I) = 30 V (1 A) = 30 W.

6.

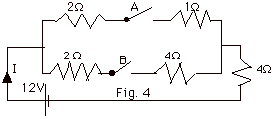
  1. When both switches are closed, the resistance of the upper branch of the parallel circuit is (2 + 1) Ω = 3Ω  and that of the lower branch is
    (2 + 4) Ω = 6Ω.

    For the parallel group,  1/Req = 1/3 Ω + 1/6 Ω  and  Req = 2Ω.

    The total resistance of the circuit is (2 + 4) Ω = 6 Ω  and
    I = 12 V/6 Ω = 2 A.

  2. If only switch A is closed, the bottom part of the parallel grouping is not in the circuit. The total resistance of the circuit is (2 + 1 + 4) Ω  and
    I = 12/7 A.

  3. If only switch B is thrown, the top part of the parallel grouping is not in the circuit. The total resistance of the circuit is (2 + 4 + 4) Ω   and
    I = 12V/10 Ω = 1.2 A.

7.


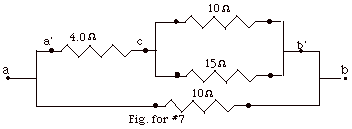
In the Fig. for #7, the 10 Ω resistance is wired in parallel with the 15 Ω resistance from c to b’. This parallel grouping is then wired in series with 4.0 resistor between a’ and b’. Finally this grouping is wired in parallel with another 10 Ω resistor.

1/Rcb’ = 1/10 Ω + 1/15 Ω = (3 +2)/30 Ω.
Rcb’ = 6 Ω.
Rab’ = (6 + 4) Ω = 10 Ω.
1/Rab = 1/10 Ω + 1/10 Ω = 2/10 Ω.
Rab = 5.0 Ω


8.



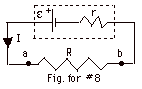
For the circuit in Fig. for #8 above,   I= ε/(r + R).

For  I = 6.0 A and R = 2.0 Ω,
6.0 A = ε/(r + 2.0 Ω)       (Equation 1)
For  I = 3.0 A and R = 7.0 Ω,
3.0 A = ε/(r + 7.0 Ω)      (Equation 2)
From Eq. 1:  ε = 6.0A r + 12 V.  From Eq. 2:  ε = 3.0A r + 21V.
Thus, 6.0A r + 12 V = 3.0A r + 21 V.   r = 9.0V/3.0 A = 3.0 Ω.
Substituting r back into Eq. 1,  6.0 A = ε/(3.0 + 2.0) Ω.    ε = 30 V.

9.



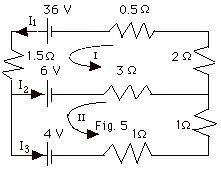
From conservation of charge,
I1 = I2 + I3  or  I3 = I1 - I2    (Equation 1)
For loop I,
36 V - I1(0.5 + 2 + 1.5) Ω- 6 V - I2(3 Ω) = 0   or
30 A = 4I1 + 3I2       (Equation 2)
For loop II,
6 V + (3 Ω)I2 - 4 V - (2 Ω)I3 = 0   or
2A = 2I3 - 3I2     (Equation 3)
Substitute Eq. (1) into Eq. (3):
2A = 2(I1 - I2) -3I2   or   2A = 2I1 - 5I2      (Equation 4) 
2 x Eq. 4 equals:                 4A = 4I1 - 10I2           (Equation 5)

Eq. 2 - Eq. 5 equals:          26A = 13I2     or    I2 = 2A.

Then from Eq. 2:               30A = 4I1 + 3(2A)   and   I1 = 6 A.

From Eq. 1,   I3 = 6A - 2A = 4A.

10.



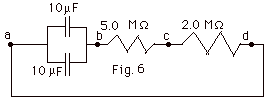
Given q(t) = Qi e-t/RC.  When t = RC,  q (RC) = Qi e -RC/RC = Qi e-1 = Qi/e.
The time constant for the circuit is RC.
  1. In Fig. 6 above, the two capacitors are in parallel. For capacitors in parallel, the equivalent capacitance is the sum of the capacitances.
    Cab = (10 + 10)µF = 20µF = 20 x 10-6 C/V.
    The two resistances are in series. The equivalent resistance of resistances in series is the sum of the resistances.
    Rbd = (5.0 + 2.0)MΩ= 7.0 MΩ = 7.0 x 106 V/A.
    The time constant =
    RC = 7.0 x 106 V/A x 20 x 10-6 C/V = 140 C/A = 140 s.
  2. q(t) = Qie-t/RC.  For Qi = 100 µC and q = 50µC, q/Qi = 1/2 = e-t/RC
     or  et/RC = 2. Taking log of both sides of this equation,  t/RC = ln 2.
    t = RC ln 2 = 140 s (0.693) = 97 s.

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
August 8, 2002
April 23, 2003