Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 106

Answers - Electric Fields

1.
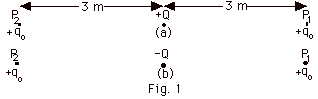
  1. The magnitude of the force of +Q or -Q on qo at r = 3 m is FqQ = kQqo/r2 = (9.0 x 109 N-m2/C2)(2 x 10-6 C)(10-12 C)/(9 m2) = 2 x 10-9 N.

    The force of +Q on +q0 at

    1. P1 is to the right since +Q repels +qo and urges it to the right

    2. P2 is to the left since +Q repels +qo and urges it to the left.

  2. The force of -Q on + qo at

    1. P1 is to the left since -Q attracts +qo and urges it to the left

    2. P2 to the right since -Q attracts +qo and urges it to the right.

2.
By definition, the direction of the electric field is the direction in which a positive test charge is urged. The magnitude of the electric field at a point P is equal to the electric force Fe on a test charge qo divided by the test charge.

For all points in Fig. 1 above, the magnitude of the electric field = (Fe)/qo = (kQqo/r2)/qo = kQ/r2 = (9 x 109 N-m2/C2)(2 x 10-6 C)/9 m2 = 2 x 103 N/C.
  1. In Fig. 1a, the electric field at P1 is to the right because a positive test charge there would be urged to the right.  At P2 the electric field is to the left because a positive test charge there would be urged to the left.

  2. In Fig. 1b, the electric field at P1 is to the left because a positive test charge there would be urged to the left.  At P2 the electric field is to the right because a positive test charge there would be urged to the right. Do not use the sign of a charge setting up a field to determine the direction of a field. Go to the point, imagine placing a positive test charge there, and ask what direction the test charge would be urged by the charge setting up the field.

3.


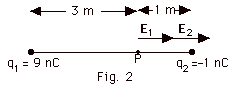
  1. In general the electric field E due to a point charge Q a distance r from the point where you wish to find the field is given by
    E = (9 x 109 N-m2/C2)Q/r2.
    For q1 in Fig. 2, E1 = (9 x 109 Nm2/C2)(9 x 10-9 C)/(3 m)2 = 9 N/C to the right because if a positive test charge is placed at P, q1 would urge it to the right.  E2 = (9 x 109 N-m2/C2)(1 x 10-9 C)/ (1 m)2 = 9 N/C to the right because if a positive test charge is placed at P, q2 would urge it to the right. The resultant field at P is E = (9 + 9) N/C = 18 N/C to the right. Again notice the importance of not using the negative sign of the charge in finding the field. If you had used the negative sign, you might have said the field due to q2 was to the left.

  2. If q2 = +1 nC,  the electric field due to q2 at P is 9 N/C to the left. Now taking to the right as positive, the resultant field at P is E = (9 - 9) N/C = 0.

4.


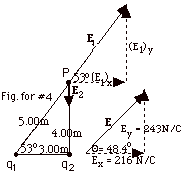
In Fig. for #4 above, the hypotenuse of the triangle = (9.00 + 16.00)1/2 m = 5.00 m.

The field due to q1,  E1 = q1/4πεor12 = 9 x 109 N-m2/C2(10-6 C/25.0m2)
= 360 N/C.  The direction of E1 is shown in Fig. for #4.

E2 = 9 x 109 N-m2/C2(0.0800 x 10-6 C/16.00 m2) = 45 N/C,  and
E2 = -45 j N/C, as shown in Fig. for #4.

Taking components of E1,  (E1) x = E1 cos 53o = 360 N/C (0.60) = 216 N/C,
and (E1)y = E1 sin 53o= 360 N/C (0.80) = 288 N/C.  The component of the resultant E in the y direction Ey = (E1)y + (E2)y = (288 - 45) N/C = 243 N/C.

E = (216 i + 243 j)N/C.   E = {(216)2 + (243)2}1/2 = 325 N/C.
tan Θ = 243/216.  Θ = 48.4o with X-axis.

5.


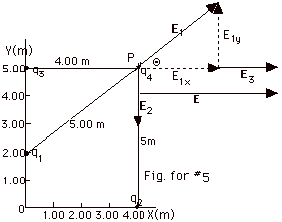
  1. In the Fig. for #5 above,  E1 represents the electric field due to
    q1 = 5.00 x 10-6 C,  which is r = 5.00 m from P.

    E1 = kq1/r2 = 9 x 109 N-m2/C2 (5.00 x 10-6C)
                                         25.0 m2
    = 1.80 x 103 N/C.

    E1x = E1 cos Θ= 1.80 x 103 N/C (0.800) = 1.44 x 103 N/C.
    E1y = E1 sin Θ=1.80 x 103 N/C (0.600) =1.08 x 103 N/C.

    In the Fig. for #5 above, E2 represents the electric field due to
    q2 = -3.00 x 10-6 C, which is a distance of r2 = 5.00 m from P.

    E2 = kq2/r2 = 9 x 109 N-m2/C2 (3.00 x 10-6)/25.0 m2 = 1.08 x 103 N/C
    in the negative Y direction (Fig. for #5).

    E2x = 0 and  E2y = -1.08 x 103 N/C.

    In the Fig. for #5,  E3 represents the electric field due to
    q3 = 1.60 x 10-6 C, which is a distance of r3 = 4.00 m from P.

    E3 = kq3/r3 = 9 x 109 N-m2/C2 (1.60 x 10-6)/16.0 m2 = 0.900 x 103 N/C
    in the positive X direction as shown in Fig. for #5.

    E3x = 0.900 x 103 N/C  and  E3y = 0.

    Let the total electric field = E.
    Ex = E1x + E2x + E3x = (1.44 + 0 + 0.90)103 N/C = 2.34 x 103 N/C.
    Ey = E1y + E2y + E3y = (1.08 -1.08 + 0)103 N/C = 0.  The resultant electric field is totally in the +X direction and it is equal to 2.34 x 103 N/C.

  2. The force on q4 at P = q4E = (2.0 x 10-6 C)(2.34 x 103 N/C) =
    4.68 x 10-3 N to the right.

6.




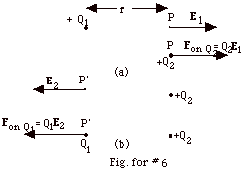
In Fig. for #6a above, we think of Q1 setting up a field E1 at P, where E1 = kQ1/r2 to the right. When Q2 is placed at P, it experiences a force Fon Q2, where Fon Q2 = Q2E1 = kQ1Q2/r2 to the right. In Fig. for #6b, we think of Q2 setting up a field E2 at P’, where E2 = kQ2/r2 to the left. When Q1 is placed at P’, it experiences a force Fon Q1, where Fon Q1 = Q1E2 = kQ1Q2/r2 to the left. This is the same result of the force on Q2 due to Q1 and the force on Q1 due to Q2 found from Coulomb's law.

7.

The electric field due to the positive point charge depends inversely upon the square of the distance from the positive point charge. A negative charge placed in the electric field of the positive point charge will experience a force that depends on the electric field. Since the field varies with the distance from the positive charge, the force F on the negative charge depends on the distance. The acceleration experienced by the negative charge will not be constant.
a = F/m.

8.


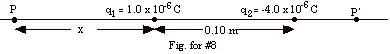
First we decide that the point where the electric field is zero cannot be between the two charges because at any point between them the electric field due to either charge is to the right so that the electric fields would add rather than cancel. The field also cannot be to the right of charge q2 at some point P'. Although the field due to q2 at P' is to the left and the field due to q1 to the right, the field due to q1 cannot cancel the field due to q2 because q2 is closer to P' than q1 and charge q2 is greater than q1. For point P, the field due to q1 is kq1/x2 to the left and the field due to q2 is kq2/(x + 0.10 m)2 to the right. The field at P is zero if
kq1/x2 = kq2/(x + 0.10 m)2  or
1.0 x 10-6 C/x2 = 4 x 10-6 C/(x + 0.10m)2  or
(x + 0.10 m)2 = (4.0/1.0)x2.         (Equation 1)
Taking the square root of both sides of Eq. 1,
x + 0.10 m = 2.0 x  and  x = 0.10 m.

9.
  1. The number of field lines is proportional to the electric flux which is proportional to the charge enclosed by the Gaussian surface. If the field lines leave the point charge, the net enclosed charge is positive. If the field lines enter the Gaussian surface the net charge enclosed is negative. The ratio of the the field lines give the ratio of the charge.

    q1/q2 = 10 μC/q2 = 15/75  or  q2 = 50 μC.

    Since the field lines enter the Gaussian surface,  q2 = -50 μC.


  2. If the field lines point out of the Gaussian surface it means that the net charge is positive. In other words, the surface could enclose some negative charge, but there are more positive charge than negative so that the net charge enclosed is positive.

10.


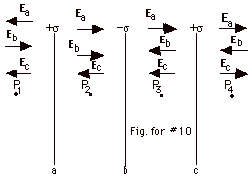
The electric field due to an infinite sheet of charge is σ/2 εo. The direction of an electric field at a point P is that in which a positive test charge placed at that point would be urged. As shown in Fig. for #10 above,
  1. at point P1 the electric field due to the sheet on the left Ea is to the left, the electric field due to the center sheet Eb is to the right and the electric field due to the sheet on the right Ec is to the left. Taking to the right to be positive, the electric field is to the left with magnitude E (at P1) =
    -σ/2 εo + σ/2 εo - σ/2 εo = - σ/2 εo.
  2. At point P2 the electric field due to the sheet on the left Ea is to the right, the electric field due to the center sheet Eb is to the right and field due to the sheet on the right Ec is to the left. Taking to the right to be positive, the E is to the right with magnitude E (at P2) =
    +σ/2 εo + σ/2 εo - σ/2 εo = + σ/2 εo.
  3. At point P3 the electric field due to the sheet on the left Ea is to the right, the electric field due to the center sheet Eb is to the left and the electric field due to the sheet on the right Ec is to the left. Taking to the right to be positive, the electric field is to the left with magnitude E (at P3) =
    σ/2 εo - σ/2 εo - σ/2 εo = - σ/2 εo .
  4. At point P4 the electric field due to the sheet on the left Ea is to the right, the electric field due to the center sheet Eb is to the left and the electric field due to the sheet on the right Ec is to the right. The electric field is to the right with magnitude E (at P4) =
    σ/2 εo - σ/2 εo + σ/2 εo = σ/2 εo.

11.




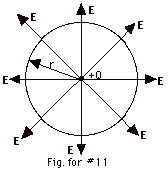
In Fig. for #11 above, a hypothetical sphere of radius r and surface area 4 πr2 is drawn around +Q. The electric field E is perpendicular to this hypothetical sphere. Thus, number of electric field lines/area = E or number of electric field lines = E(area) = (kQ/r2)(4 πr2) = (k)Q(4 π) = (1/4πεo)Q(4 π) = Q/ εo.

12.


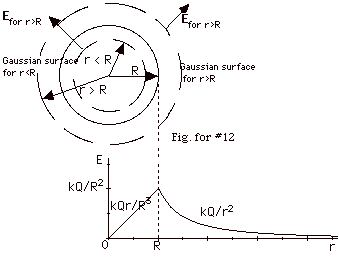
In the Fig. for #12 above, the spherical Gaussian surface for r < R and r > R are drawn with dashed lines. By symmetry, the electric field at both surfaces is perpendicular to the surfaces. If you rotate the sphere of charge, you should not expect the electric field direction on the Gaussian surface to change. This will only be true if the field is radially outward. E is normal to the surface, that is, the angle between E and dA is zero and E . dA = E dA cos 0o = E dA.  If you rotate the charged sphere the magnitude of E on the Gaussian surface can not change.  E is constant everywhere on the surface.

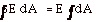= E 4 πr2

  1. For r < R, the Gaussian surface does not enclose the total charge Q.

    Charge/volume = Q/V = ρ= Q/(4 πR3/3), where 4 πR3/3 = V = the volume of the charged sphere. The charge enclosed by a Gaussian surface with r < R
    = ρ (Volume of the Gaussian surface)
    = {Q/(4/3 πR3}(4/3 πr3) = Qr3/R3
    For r < R,   E (Area of Gaussian Surface) = charge enclosed/ εo,

    which becomes
    E4 πr2 = Qr3/R3 εo  or  E = Qr/4πεoR3 = kQr/R3    (Equation 1)


  2. For r > R, the Gaussian surface encloses all the charge Q, E4 πr2 = Q/ εo.                      or                 E = Q/4πεor2 = kQ/r2       (Equation 2)
    If you let r = R in Eq. 1 or in Eq. 2, you get E = kQ/R2. Both expressions are equivalent at r = R, so we may write for r ≤ R,  E = kQr/R3 = (kQ/R3)r, that is,  E = constant times r, so E is directly proportional to r, and a plot of E vs. r for r ≤ R yields a straight line. For r ≥ R,  E = kQ/r2 for a sphere of radius R with a uniform distribution of charge. Notice for r ≥ R, the sphere “acts” like a point charge Q located at the center of the sphere.  A plot of E as a function of r is shown in the above figure.

13.


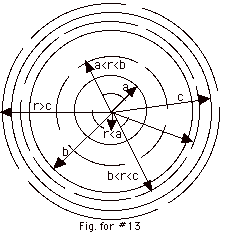
  1. In the figure above, the Gaussian surfaces for  r < a,   a < r < b, 
    b < r < c,  and  r > c  are shown by dashed surfaces. Using the same arguments we did in Problem 12, we establish that the electric field is perpendicular to the Gaussian surfaces and constant everywhere on them. The definition of a conductor is that electrons are perfectly free to move in them. They move until there is no electric field inside the conductor, which would produce a motion of charges. Since there is no electric field inside the sphere of radius a, there can be, in agreement with Gauss' theorem, no charges enclosed by a surface inside the sphere. You can use this argument until r goes to a and decide the +Q is on the outside of the sphere of radius a. In addition, since there can be no electrical field inside the spherical shell, the Gaussian surface for b < r <c  must enclose no net charge. The - Q must be on the inner surface of the spherical shell of radius b and the +Q must be on the outside of the shell of radius c. This gives the net charge on the shell equal to +Q - Q = 0. From all of this we conclude by Gauss' theorem, (E)(Area of Gaussian surface) = charge enclosed/ εo.

  2. For r < a,
    E(4 πr2) = 0
    E = 0
  3. For a < r < b,
    E(4 πr2) = Q/ εo
    E = Q/4πεor2 = kQ/r2
  4. For b < r < c,
    charge enclosed = + Q - Q = 0  so
    E(Area) = 0   or   E = 0
  5. For r > c
    E(4 πr2) = (Q - Q + Q)/ εo = Q/ εo
     E = Q/4πεor2 = kQ/r2

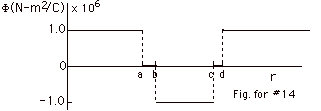
14.


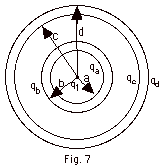
A Gaussian surface surrounding the point charge q1 encloses an electric flux Φ from  r = 0  to  r = a  equal to
(charge enclosed)/ εo =
8.85 x 10-6 C/8.85 x 10-12 C2/N-m2 = 106 N-m2/C.
  1. The electric flux Φ from  r = a  to b must be zero because this region is inside a conductor. For the flux to be zero, a Gaussian surface there can enclose no charge. Thus qa = - q1 = -8.85 x 10-6 C.

  2. Since the net charge on the inner shell is -17.70 x 10-6 C = qa + qb,
    qb = -17.70 x 10-6 C - qa
         = -17.70 x 10-6 C - (-8.85 x 10-6 C)
         = -8.85 x 10-6 C.
    The electric flux from b to c = charge enclosed/ ε0 = (q1 + qa + qb)/ εo
     =(8.85 - 8.85 - 8.85)10-6C/8.85 x 10-12 C2/N-m2 = -106 N-m2/C.

    The electric flux inside the outer shell from c to d = 0 = charge enclosed/ ε0 = (q1 +qa + qb + qc)/ εo or (8.85 -8.85 -8.85)10-6 C = -qc and qc = 8.85 x 10-6 C.

    Since the net charge on the outer shell is +17.70 x 10-6 C, = qc + qd = 8.85 x 10-6 C + qd,  qd = 8.85 x 10-6 C.

    From d to infinity, the electric flux equals (charge enclosed)/ εo
    =(q1 +qa + qb + qc + qd)/ εo
    =(8.85 - 8.85 - 8.85 + 8.85 + 8.85)10-6 C/8.85 x 10-12 C2/N-m2
    = 106 N-m2/C.


  3. From 0 to a, Φ= 106 N-m2/C.
    From a to b, Φ= 0.
    From b to c, Φ = -106 N-m2/C.
    From c to d, Φ= 0.
    From d to infinity, Φ = 106 N-m2/C.

15.


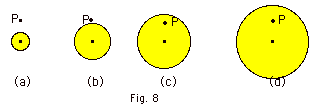
  1. The charge density = total charge/volume ρ = Q/(4 πR3/3). Each sphere has the same total charge Q. The sphere in Fig. 8d above has the largest radius. The charge density ρ is inversely proportional to the cube of the radius. The ranking of charge densities with the greatest first is Fig. 8a > Fig. 8b > Fig. 8c > Fig. 8d.

  2. For a point P outside of the charge distribution, as in Fig. 8a and Fig. 8b, all the charge acts at the center and the electric field for both is E = kQ/r2 where r is the distance from the center of the sphere to point P. The electric field at P for Fig. 8a and Fig. 8b are equal. For Fig. 8c and 8d, a Gaussian spherical surface drawn with a radius r from the center of the sphere to P would not enclose the total charge so the fields would be smaller than those for Fig. 8a and Fig. 8b. Since such a Gaussian surface would enclose more charge for Fig. 8c than for Fig. 8d, the electric field would be greater for Fig. 8c than for Fig. 8d. As we found in Problem 12, for  r < R,  E = kQr/R2. The rankings for highest field are Fig. 8a and Fig. 8b tie for first, Fig. 8c is third, and Fig. 8d comes in last.

16.

The tangent to an electric field line at any point gives the direction of the electric field at that point. If two electric field lines intersected, the tangent to the field lines at that point and the electric field at that point would have different directions and that is not possible.

17.


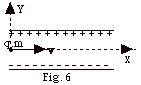
  1. Fe = qE = (3.2 x 10-19 C)(20 x 102 N/C) = 6.4 x10-16 N.  Since the electric field is down and the charge is positive, the electric force is down.

  2. The acceleration due to this force a = Fe/m = 6.4 x 10-16 N/1.6 x 10-27 kg = 4.0 x 1011 m/s2 down.

  3. The acceleration due to the gravitational force = g = 9.8 m/s2 down.

  4. Since the acceleration due to the gravitational force is much smaller than the acceleration due to the electric force we can ignore it and say ay = 4.0 x 1011 m/s2. There is no acceleration in the X-direction, that is, ax = 0.

    x(t) = xo + voxt + 1/2 axt2.  Since ax = 0, vox = v = 4.0 x 106 m/s,
    and taking xo = 0 with the X-Y axes as shown in Fig. 6 above,
    x = voxt  or  t = x/vox = 0.80 m/4.0 x 106 m/s = 2.0 x 10-7 s.

  5. y(t) = yo + voyt + 1/2 ayt2 = y(2.0 x 10-7 s) =
    0 + 0 + 1/2(4.0 x 1011m/s2)(2.0 x 10 - 7 s)2 = 8.0 x 10-3 m.

18.
  1. The force (Fe)p on the proton is in the direction of the electric field and equal to qE.  The acceleration ap of the proton is in the same direction as the force and equal to (Fe)p/m = eE/m, where m is the mass of the proton.

  2. The velocity vp and the displacement xp of the proton are in the same direction as the acceleration.   vp(t) = vo + apt = 0 + (eE/m)t.
    xp(t) = xo + vot + 1/2 apt2 = 0 + 0 +1/2(eE/m)t2.

19.

The force (Fe)α on the alpha particle is in the direction of the electric field and equal to 2eE.  The acceleration aα of the alpha particle is in the same direction as the force and equal to (Fα)/4m = 2eE/4m, where m is the mass of the proton. The velocity vα and the displacement xα are in the same direction as the acceleration.

Vα(t) = vo + aαt = 0 + (2eE/4m)t = vp/2.
xa(t) = xo + vot + 1/2 aαt2 = 0 + 0 +1/2(2eE/4m)t2 = xp/2.

20.

The force on a charged particle q in an electric E is Fe = qE. The electric force is independent of the speed of the particle. Whether the particle is initially at rest or moving with a velocity v, the force on it is qE.

21.
The electric field E due to a very long, uniformly charge wire is λ/2πεor  radially outward for a positive charge per unit length λ.  An electron moving around the wire experiences a force in toward the axis of the wire = eE = e λ/2 πr εo.  This force in toward the center produces a centripetal acceleration.
Fnet = ma
e λ/2 πr εo = mv2/r
(e λ/2 πm εo) = v2
1.6 x 10-19 C(2.5 x 10-9 C/m)/2 π(9.1 x 10-31 kg)(8.85 x 10-12 C2/N-m2) = v2
 v = 2.8 x 106 m/s.

22.




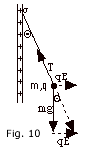
The electric force on the sphere of charge q is Fe = qE.  The electric field due to the sheet E = σ/2 εo.  For the sphere to remain at rest, the net force on it must equal zero,  that is  T + mg + qE = 0,  where T is the tension in the string.  From the geometry of the figure, we see that tan Θ = qE/mg = (qσ/2 εo)/mg or
σ = 2 εomg tan Θ/q.

23.


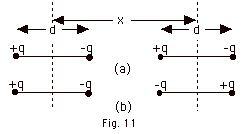
Taking to the right to be positive for the force of the charges in the dipole at the left on the charges in the dipole at the right in Fig. 11a above,

F = kq2/x2 - kq2/(x +d)2 - kq2/(x - d)2 + kq2/x2

Putting the above expression over the common denominator
x2(x2 + d2) (x2 - d2) gives:

F = {kq2/[ x2(x + d)2 (x - d)2]}{2(x + d)2 (x - d)2 - x2(x - d)2 - x2(x +d)2}
  = {kq2/[ x2(x2 - d2)2} {2(x2 – d2)2 - x2(x - d)2 - x2(x +d)2}
  = {kq2/[ x2(x2 - d2)2} {2(x4 – 2x2d2 + d4) - x2(x2 - 2dx + d2)
         - x2(x2 - 2dx + d2)}
  = {kq2/[ x2(x2 - d2)2} {-6x2d2 + 2d4}

Since 6x2d2 > 2d4, the net force on the dipole to the right will be to the left. By Newton's third law, the net force on the dipole to the left will be equal in magnitude, but to the right.

For Fig. 11b, again taking to the right to be positive for the forces of the charges in the dipole at the left on the charges of the dipole at the right,

F = = -kq2/x2 + kq2/(x +d)2 + kq2/(x -d)2 - kq2/x2.

The magnitude of the force is the same as in (a), but opposite in direction. Notice for x >> d, |F| = |{kq2/[ x2(x2 - d2)2} {-6x2d2 + 2d4}| reduces to 6kq2d2/x4 = 6kp2/x4, where p = the dipole moment.

24.




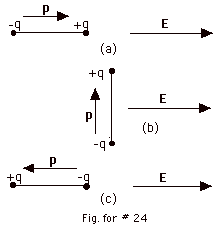
In general the torque τ= p x E

τ = pE sin p, E

  1. For p parallel to E (Fig. for 24a above)
    p, E = 0, sin 0o = 0,  so  τ= 0.

  2. For p perpendicular to E (Fig. for 24b above)
    p, E = 90o, sin 90o = 1,  so τ= pE =[qd](E)
             = [(3.2 x 10-19 C)(2 x 10-9 m)](5.0 x 105 N/C)
             = 3.2 x 10-22 N-m.
    The direction of the torque is into the page.

  3. For p antiparallel to E (Fig. for 24c above)
    p, E = 180o, sin 180o = 0,  so τ= 0.

25.
  1. You can find an electric field due to a distribution of charges by

    1. finding the electric field due to each point individually and then adding them vectorally or

    2. using Gauss's theorem if the charge distribution has spherical, cylindrical, or plane symmetry.

  2. Once you know an electric field E, you can find the electric force Fe on a charge q from Fe = qE.

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
August 8, 2002
April 22, 2003