Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 106

Answers - Induction

1.



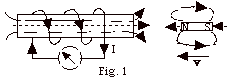
The left side of the magnet is a north-seeking pole and the right side is a south-seeking pole. As the bar magnet advances toward the coil of wire, its magnetic field lines to the left are thrust into the coil. To oppose the change that produced it, the magnetic field lines of the induced current must be to the right. If you curl the fingers of your right hand in the direction of the current, your thumb points in the direction of the magnetic field lines produced in the coil as shown in Fig. 1 above.

2.



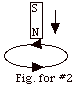
As the magnet moves toward the coil, it induces a current in the coil in the direction shown in Fig. for #2 above. The opposing magnetic field of the induced current slows down the magnet. The magnet experiences an acceleration down due to the gravitational force and and an acceleration up due to the magnetic force of the induced field. Since the rate of change of the magnetic flux due to the magnet varies with time, the magnetic force will vary and the acceleration is not constant.

3.



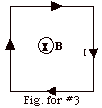
ΦB = B . A = BA cos 0o = BA
ε = - ΔΦB/ Δt = - ( ΔB/ Δt)A = - [(0.040 -0.080)N/A-m/(2.0 s)]4.0 m2
  = - 0.080 N-m/C = - 0.080 V
I = ε/R = 0.080 V/0.04 Ω = 2 A

With the magnetic field into the page and decreasing, the sense of the current will be such to oppose the change that produced it or clockwise. A clockwise-induced current produces a magnetic field into the page and opposes the decreasing external magnetic field.

4.



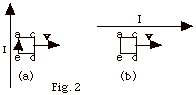
The current in the very long wire produces a magnetic field into the loop of wire acde in Fig. 2 above. This field decreases with distance from the wire. As the coil in Fig. 2a moves away from the current-carrying wire, the magnetic field due to the wire through the coil decreases. To oppose this change, the induced current in the loop acde is clockwise. A clockwise current will produce a field into the page. When the loop in Fig. 2b moves parallel to the current I of the long wire, there is no change in the magnetic field through the loop acde and there is no induced current in it.

5.

  1. The length of the chain = 0.40 π m = 2 πr and r = 0.20 m.
    A = πr2 = π(0.040 m2).

    Ignoring the minus sign,
    ε = ΔΦ/ Δt
      = Δ(BA)/ Δt
      = [(0.060 - 0.010)N/A-m](0.040 π m2)/0.50 s
      = 0.004 π V.
    I = ε /R = 0.004 π V/0.001 Ω = 4 π A.

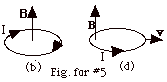
  2. The sense of the current is shown in Fig. for #5b above. Notice the induced currrent produces a magnetic field that opposes ΔB.

  3. The chain contracts "trying" to keep the increasing flux out of the loop.

  4. ε = ΔΦ/ Δt = Δ(BA)/ Δt
      = [(0 - 0.060)N/A-m](0.040 πm2)/0.30 s = - 0.008 π V.

    I = ε /R = 0.008 π V/0.001 Ω = 8 π A.

    The diagram is shown in Fig. for #5d above. At the left end of the loop, the current I is out of the page, the magnetic field B is up, and the force on the loop is to the left. The magnetic force hinders the withdrawal of the chain from the field.

6.



  1. Φ = BA cos Θ = BA cos ωt. The magnetic flux equals the component of the magnetic field perpendicular to the area times the area.

  2. ε = - dΦ/dt = + ωBA sin ωt = ωBA sin Θ.

  3. The magnetic flux is a maximum when Θ is 0o or ± (180o). This occurs when the plane of the coil is perpendicular to the magnetic field.

  4. The emf is a maximum when Θ is π/2 (90o) or 3 π/2 (270o). This occurs when the plane of the coil is parallel to the magnetic field and the magnetic flux is changing most rapidly.

7.



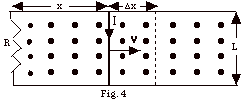
  1. The initial magnetic flux (ΦB)i = B(area) = B(xL).

  2. The later magnetic flux = B(x + Δx)L.
    The change in flux = ΔΦ= BL{(x + Δx) -x} = BL Δx.

  3. The electromotive force = ε = ΔΦ/ Δt = BL( Δx/ Δt) = BLv.

  4. I haven't used the minus sign because we find the sense of the current from Lenz's law. The sense of the induced current is such to oppose the change that produces it. As the rod moves to the right, the magnetic flux out of the page increases. To oppose this, the induced current must be clockwise. A current clockwise will produce a field into the page. If you curl the fingers of your right hand clockwise, your thumb points into the page.

  5. The current I = ε/R = BLv/R.

  6. Power dissipated in the resistance R = I2R = (BLv/R)2R = B2L2v2/R,
    since I = ε/R = BLv/R.

  7. In Fig. 4 above, the induced current is clockwise, which means positive charge moves down through the bar of length L. The force on the current carrying bar due to the magnetic field B is Fm = I( L x B).  L is taken in the direction of the current or down. B is out of the page, so Fm can be neither in or out nor up or down. It must be to the right or the left. If you rotate vector L into vector B, you find Fm is to the left. The external agent must exert a force F equal in magnitude to Fm to move the rod with a constant velocity.  F = Fm = ILB sin 90o = ILB = (BLv/R)LB = B2L2v/R.

  8. Power = work/time = (force x distance)/time = force x (distance/time) = force x v. Power generated by external agent = (B2L2v/R)v = B2L2v2/R.

  9. Notice that the answers to (f) and (h) are the same, as, of course, they should be if you believe in conservation of energy and all those good things. The external agent must do work in order to produce the induced emf and current. Lenz's law is just a statement of conservation of energy.

8.

  1. As the bar slides down, the magnetic flux into the page increases. To oppose this, the induced current must be to the right in the bar. The induced current then produces a magnetic field out of the page inside the loop.

  2. The "motional emf" = BLv.  I = ε/R = BLv/R.  The magnetic force on the bar of length L is Fm = (I)LB sin 90o = (BLv/R)LB(1) = B2L2v/R. For a current to the right in a field into the page the force on the bar is up. For constant velocity, Fnet = B2L2v/R - mg = 0  and  v = mgR/B2L2 = 0.50 kg(9.8 m/s2)(0.01 N-m/A-C)/(0.20 N/A-m)2(0.5 m)2 = 4.90 m/s.

9.





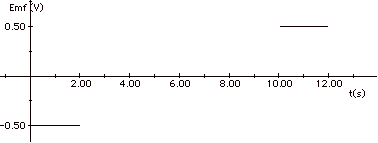
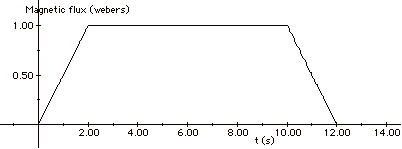
After 1 s, one-half of the loop is in the magnetic field so the magnetic flux = BA = (1T)(0.5m2) = 0.5 Wb.

After 2 s, the entire loop is in B:  ΦB = 1 Wb.

From  t = 2s  to  t = 10 s,  the entire loop is in the field.

At  t =10 s, the front edge of the loop reaches the edge of the field boundary.

At  t = 11 s, only half the loop is in the field, and at  t = 12 s  none of the loop is in the field.

From  t = 12 s on the flux is zero.

Since the emf = - dΦB/dt,  you find the emf from the negative slope of the
ΦB vs t  graph, as shown in the figures above. As the loop enters the magnetic field, the sense of the induced current is clockwise in the loop producing a magnetic field into the page to oppose the change that produced it.  As it leaves the field, the current is counterclockwise.

From  t = 0  to  t = 2 s, and from  t = 10 s  to  t = 12 s,
I = ε/R = 0.50 V/0.01Ω = 50 A.

From  t = 2s  to  t = 10 s,  I = 0.

10.



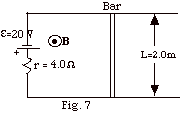
For the bar to experience no net force, the net emf in the circuit, ε = 20 V of the battery, is balanced by an opposing emf due to the change in magnetic flux in the loop of Fig. 7 above.

20 V = 20 J/C = 20 N-m/C = ΔΦ/ Δt = Δ(BA)/ Δt
        = [(1.10 - 0.10)N-s/C-m][(2.0 m)(x)]/0.10 s

x = 1.0 m

11.
To oppose the change which produced it, as the magnetic field increases out of the page, the bar must move to the right to increase the area through which the field passes so the "back" emf will increase to 20 V.

20 V = 20 J/C = 20 N-m/C = ΔΦ/ Δt = Δ(BA)/ Δt = Δ(BLx)/ Δt = BLv
        = [1.10 N-s/C-m][(2.0 m)(v)]

v = 9.1 m/s

12.



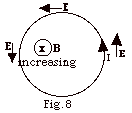
We can, and do, think of a changing magnetic flux producing an electric field. In Fig. 8 above the electric field line is counterclockwise. At any point the electric field is tangent to the circle. This electric field produces a counterclockwise current in the wire opposing the change in the magnetic field. Even if the wire is not there, the electric field with field lines counterclockwise is produced by a magnetic field into the page and increasing.

13.



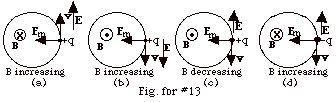
For a particle to move in a circle, there must be a force in to the center of the circle to produce the centripetal acceleration.
  1. In Fig. for #13a, with the magnetic field B into the page, the magnetic force Fm will be in to the center of the circle when the charged particle travels counter-clockwise. If the magnetic field into the page is increasing, the induced electric field E will always be in the same direction as the velocity of the particle and its velocity will increase.

  2. In Fig. for #13b, with the magnetic field B out of the page, the magnetic force will be in to the center of the circle when the charged particle travels clockwise. If the magnetic field out of the page is increasing, the induced electric field E will always be in the same direction as the velocity of the particle and its velocity will increase.

  3. In Fig. for #13c, with the magnetic field B out of the page, the magnetic force will be in to the center of the circle when the charged particle travels clockwise. If the magnetic field out of the page is decreasing, the induced electric field E will always be opposite to the direction of the velocity of the particle and its velocity will decrease.

  4. In Fig. for #13d, with the magnetic field B into the page, the magnetic force will be in to the center of the circle when the negatively charged particle travels clockwise. If the magnetic field into the page is increasing, the induced electric field E will always be in the opposite direction to the velocity of the electron and its velocity will increase.
Remember the direction of the electric field is the direction in which a positive charge is urged. An electric field up exerts a force down on an electron.

14.




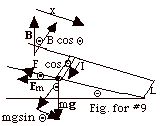
dΦB = B . dA = B xL cos Θ
ε = - dΦB/dt = - B (dx/dt)L cos Θ = - BvL cos Θ
I = ε/R = BvLcos Θ/R
Fm = I(L x B)
Fm = ILB sin 90o = ILB = [BvL cos Θ/R](LB) = (BL)2v cos Θ/R

The direction of the magnetic force is to the left. The component of the magnetic force up the plane equals
Fm cos Θ = [(BL)2v cos Θ/R]cos Θ= (BL)2 v cos2 Θ/R.
The component of the gravitational force down the plane = mg sin Θ.

For a constant velocity,  Fnet = mg sin Θ - (BL)2 v cos2 Θ/R = 0   or
v = mgR sin Θ/(BL cos Θ)2.

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
August 8, 2002
April 23, 2003