Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 107

Outline - Simple Harmonic Motion
  1. Definition of Simple Harmonic Motion

    1. Simple harmonic motion occurs when the force F acting on an object is directly proportional to the displacement x of the object, but in the opposite direction.

    2. Mathematical statement F = - kx

    3. The force is called a restoring force because it always acts on the object to return it to its equilibrium position.


  2. Descriptive terms

    1. The amplitude A is the maximum displacement from the equilibrium position.

    2. The period T is the time for one complete oscillation. After time T the motion repeats itself. In general x(t) = x (t + T).

    3. The frequency f is the number of oscillations per second. The frequency equals the reciprocal of the period.  f = 1/T.

    4. Although simple harmonic motion is not motion in a circle, it is convenient to use angular frequency by defining ω = 2 πf = 2 π/T.


  3. Example of Simple Harmonic Motion - mass at end of spring



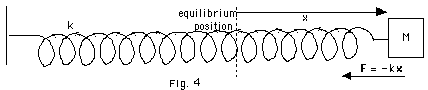
    1. When the object is at its equilibrium position, the spring is neither stretched or compressed.

    2. Differential equation of motion

      1. Fnet = ma
          - kx = ma

      2. Since v = dx/dt, and a = dv/dt, a = d(dx/dt)/dt = d2x/dt2                     - kx = md2x/dt2  or
           d2x/dt2 +(k/m)x = 0                    (Equation 1)

      3. Solution of Equation 1 gives x as a function of t.

        If you have had differential equations, you can solve this equation. If not, the following equation can be shown to be true by experiment. In any event the solution to Equation 1 is:

        x(t) = A cos (2 πt/T + Φ) = A cos (2 πft + Φ) = A (cos ωt + Φ)
                                                                             (Equation 2)

      4. Verification of A and T in Equation 2

        1. The maximum value of cos (2πt/T + Φ) = 1. Thus the maximum value of x = A, which is the definition of A.

        2. The value of x(t) must equal the value of x(t + T) if the motion repeats itself after one period. Thus for this to be true,
          x(t) = x(t + T)
          x(t + T) = A cos [(2 πt +T)/T + Φ]
          = A cos [2 πt/T + 2 π + Φ]
          = A cos [2 πt/T + Φ]
          = x(t)
          since 2 π= 360o and cos Θ = cos (Θ + 2 π)
          so x(t) = x(t + T)
      5. Finding an expression for ω.  From Equation 2,

        1. v(t) = dx/dt = -ωA sin (ωt + Φ)

        2. a(t) = dv/dt = d2x/dt2 = -ω2 [A cos (ωt + Φ) = -ω2 (x)

        3. Substitute d2x/dt2 = -ω2 (x) into Equation 1:
          -ω2 (x) + (k/m)(x) = 0,  or ω = (k/m)1/2
        4. For mass-spring, x(t) = A cos [(k/m)1/2 t + Φ]

    3. Sample problems in 107 Problem Set for Simple Harmonic Motion: 1-4,
      11, 12.


  4. Phase angle Φ and initial conditions

    1. x(t) = A (cos ωt + Φ).  x(0) = xo = A cos Φ.   cos Φ =xo/A
      v(t) = -ωA sin (ωt + Φ). v(0) = vo = -ωA sin Φ.   sin Φ = -vo /ωA

      1. tan Φ = sin Φ/cos Φ = (-vo /ωA)/(xo/A) = -vo /ωxo
      2. sin2 Φ + cos2 Φ = (-vo /ωA)2 + (xo/A)2
         1 = (1/A2)[ (-vo /ω)2 + (xo)2]
        A2 = [ (-vo /ω)2 + (xo)2],  or  A = [(xo)2 + (-vo /ω)2]1/2

    2. Special Cases

      Find x(t) for ω = 0.350 Hz = 0.350 s-1
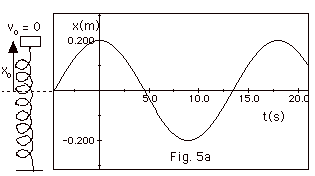
      1. When xo = 0.20 m and vo = 0

        A = [(xo)2 + (-vo /ω)2]1/2 = [(0.20 m)2 + 0]1/2 = 0.20 m
        cos Φ =xo/A=0.20 m/0.20 m = 1
        sin Φ = -vo /ωA = 0.  Φ= 0.  x(t) = 0.20 m cos 0.350 s-1t.
        Fig. 5a below shows x as a function of t with the mass at xo = A, vo = 0, and Φ = 0.



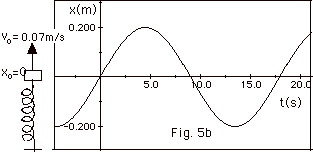
      2. When xo = 0 and vo = 0.070 m/s

        A = [(xo)2 + (-vo /ω)2]1/2 = {(0) + [(-0.070m/s)/0.35s-1]2}1/2
        = 0.20 m
        cosΦ =xo/A = 0/0.20 m = 0.
        sinΦ = -vo /ωA = -0.070m/s/(0.350s-1)(0.20m) = -1.  Φ= - π/2.
        x (t) = 0.20 m cos (0.350 s-1t - π/2)
        A plot of x as a function of t for xo = 0, vo = 0.07 m/s
        with Φ = -π/2 is shown in Fig. 5b below.




      3. When xo = 0.1(3)1/2 m and vo = 0.035 m/s

        A = [(xo)2 + (-vo /ω)2]1/2 =
        {(0.03) + [(-0.035m/s)/0.35s-1]2}1/2 = 0.20 m
        tan Φ = -vo /ωxo = -0.070m/s/(0.350s-1)(0.1√3 m) = -0.577
        Φ= - π/6
        x (t) = 0.20 m cos (0.350 s-1t - π/6)
        A plot of x as a function of t for xo = 0.1(3)1/2 m, vo = 0.035 m/s with Φ = -π/6 is shown in Fig. 5 c below.



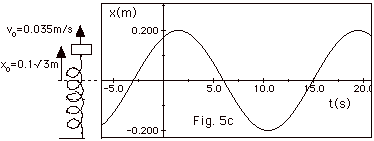
        You can work backwards to find t if you know x at that time.
        For example, find t when x = 0.10 m.
        Then 0.10 m = 0.20 m cos (0.350 s-1 t-π/6),  or
        1/2 = cos (0.350 s-1 t-π/6).
        cos 60o = cos π/3 = 1/2,  so π/3 = (0.350 s-1 t -π/6)
        or  0.350 s-1 t = π/3 + π/6 = π/2.
        t =( π/2)/(0.350 s-1) = 4.49 s.
        Check Fig. 5 c above for verification of t.

    3. Sample problems in 107 Problem Set for Simple Harmonic Motion: 10,
      14-16, 22-24.


  5. Examples of simple harmonic motion other than mass-spring

    1. The definitions of A, T, f, and ω are the same

    2. The equation of motion when maximum positive displacement occurs for t = 0 has the same form as x(t) = A cos (ωt + Φ) for example, if the motion is along an arc, the equation could be Θ(t) = Θmax cos (ωt + Φ)

    3. For different set-ups, ω is not the same.

      1. For pendulum, with L = length of pendulum,
        d2x/dt2 + (g/L)x = 0

      2. For mass-spring equation,
        d2x/dt2 + (k/m)x = 0
        For mass spring, ω= (k/m)1/2.
        You see for a pendulum ω= (g/L)1/2 = 2 πf = 2 π/T.


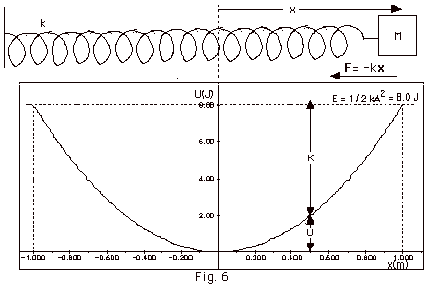
  6. For a spring with F = -kx,

    1. The potential energy function U = 1/2 kx2

    2. Total Energy E = U + K

      1. For any value of x, E = 1/2 kx2 + 1/2 mv2

        For x = ±A, v = 0, because the mass stops momentarily at both ends. At x = ±A, E = 1/2 kx2 + 1/2 mv2 becomes:

      2. E = 1/2 kA2 + 0 = 1/2 kA2

    3. Figure 6 below shows a plot of U as a function of x. The total energy
      E = 1/2 kA2 = constant.  E = U + K, as shown in Fig. 6.  U is greatest at
      x = ±A and K is greatest at x = 0.




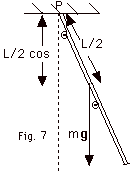
  7. Simple Harmonic Motion for Angular Motion

    Statement of the problem: Uniform rod of length L is suspended at a point P. Find the period of the oscillation for small angular displacements Θ.
    (See Fig. 7 below)



    Approach 1: The magnitude of the torque about P due to mg acting at the center of the rod is (L/2)mg sin Θ. As the rod swings counterclockwise, the torque tends to return the rod to the equilibrium position, clockwise. The torque then is -(L/2)mg sin Θ.  For small Θ, sin Θ ≈ Θ and the torque =
    -[(L/2)mg]Θ. Since all the quantities in the bracket are constants, the torque is directly proportional to the angular displacement Θ and in the opposite direction. The moment of inertia I of the rod about one end is 1/3 mL2,  or

    τP = IPα
    -[(L/2)mg]Θ = (1/3 mL2)d2Θ/d/t2
    d2Θ/dt2 + (3g/2L)Θ = 0

    Compare this with equation for mass attached to spring d2x/dt2 + (k/m)x = 0, for which ω = (k/m)1/2,  and see for this case ω = (3g/2L)1/2 and T = 2 π(2L/3g)1/2.


    Approach 2:

    The potential energy U of the rod as a function of Θ = mgL(1 - cos Θ)/2.
    K =1/2 I ω2= 1/2 (1/3 mL2) (dΘ/dt)2
    The total energy = E = mgL(1 - cos Θ)/2 + 1/2 (1/3 mL2) (dΘ/dt)2
    Since the total energy is a constant,
    dE/dt = 0 = mgL sin Θ(dΘ/dt)/2 + 1/3 mL2 (dΘ/dt)(d2Θ/dt2).
    For small Θ, (mgL/2)Θ + 1/3 mL2(d2Θ/dt2)
    or  d2Θ/dt2 + (3g/2L)Θ = 0, as before.


    Sample problems in 107 Problem Set for Simple Harmonic Motion: 26, 27.



Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
October 8, 2002
April 18, 2003