|
Outline - Work and Energy
|
|
- Definition of Work
-
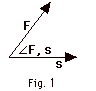 Work
= Fs cos  F,s,
where F is the force, s is the distance moved and F,s
is the angle between F and s. Work is a scalar
quantity. Since work is a scalar quantity, you are free to
use a + sign for work when the work increases the energy of
a system and a - sign for work when the work takes energy
out of the system.
- Calculation of work done by various forces
(f is the frictional force)
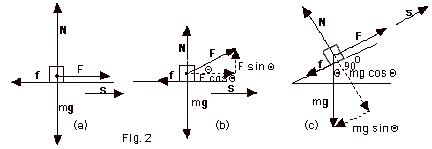
- For Fig. 2a above
- Work done by F = Fs cos F,s
= Fs cos 0o = Fs
- Work done by N = Ns cos N,s
= Ns cos 90o = 0
- Work done by mg = (mg)s cos mg,s
= (mg)s cos -90o= 0
- Work done by f = fs cos f,s
= fs cos 180o = -fs
- For Fig. 2b
- Work done by F = Fs cos F,s
= Fs cos Θ
- Work done by N = Ns cos N,s
= Ns cos 90o = 0
- Work done by mg = (mg)s cos mg,s
= (mg)s cos -90o= 0
- Work done by f = fs cos f,s
= fs cos 180o = -fs
- For Fig. 3c
- Work done by F = Fs cos F,s
= Fs cos 0o = Fs
- Work done by N = Ns cos N,s
= Ns cos 90o = 0
- Work done by mg = (mg)s cos mg,s
= (mg)s cos -(Θ
+ 90o) = -mgs sin Θ
- Work done by f = fs cos f,s
= fs cos 180o= -fs
- Sample problems in 107
Problem Set for Work and Energy: 1-6.
- Work-energy theorem
The work done by the net force equals the change in the
kinetic energy. The kinetic energy K = 1/2 mv2, where
m is the mass of the object and v its speed.
Example:
Each graph in Fig.3 below describes the one-dimensional motion
and finds the work done in each case:
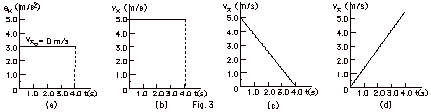
- In Fig. 3a, the area under the a versus t graph, the change
in velocity
= 3.0 m/s2 (4.0 s) = 12 m/s. Work done by net force
= change in kinetic energy = 1/2 mvf2
- 1/2 mvo2 = 1/2(5.0 kg)(12 m/s)2
- 1/2(5.0 kg)(0)2 = 360 J
- In Fig. 3b, the velocity is constant. There is no change
in kinetic energy and no work is done.
- Work done by net force = change in kinetic energy =
1/2 mvf2 - 1/2 mvo2
= 1/2(5.0kg)(0)2 -1/2(5.0kg)(5m/s)2
= -62.5 J
- Work done by net force = change in kinetic energy =
1/2 mvf2 - 1/2 mvo2
= 1/2(5.0kg)(5m/s)2 -1/2(5.0kg)(0)2
= +62.5 J
- Sample problems in 107
Problem Set for Work and Energy: 7, 9-14.
- Mechanical Energy
- Kinetic Energy K is energy of motion. For an object of mass
m moving with a velocity v,
K = 1/2 mv2
- Potential Energy U is energy of position. Potential energy
at point P equals the negative of the work done by a conservative
force in going from a point of zero potential to point P.
Every conservative force has its own potential energy function.
- Near the earth's surface, where the weight of the object
is mg, the gravitational potential energy function U =
mgh, where m is the mass of the object, g is the acceleration
due to gravity and h is the vertical height above the
zero potential energy point. You usually take the zero
of potential energy at the lowest point, unless a specific
location is given for U = 0 in the statement of the problem.
- Elastic potential energy function U = 1/2 kx2,
where k is the spring constant and x is the displacement
from the equilibrium position. The zero of potential energy
for the spring is when the mass is at the equilibrium
position, x = 0.
- The potential energy for the gravitational force Fg
= (Gm1m2/r2), where
the force is in the negative radial direction, is
U = - Gm1m2/r. The zero for this
U is when r = infinity.
|
Type of conservative force
|
Force
|
Potential Energy Function
U
|
U = 0 point
|
|
Gravitational force near
Earth's surface = a constant
|
mg
|
mgh = mgy
|
y= h = 0
|
|
Gravitational force between
two "point" objects = a variable
|
Fg = -Gm1m2r/r3
F = Gm1m2/r2
|
-Gm1m2/r
|
r = ∞
|
|
Elastic force = a variable
|
F = -kx
|
1/2 kx2
|
x = 0
|
- The total energy of a system E = U + K.
- If no non-conservative force acts on a system,
Ef = Ei, or (Uf
+ Kf) = (Ui + Ki)
- If non-conservative forces act on the system, work done
by the non-conservative forces =
(Uf
+ Kf) - (Ui + Ki)
Example:
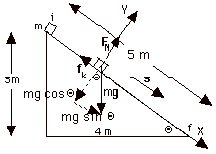
(a) An object of mass m = 2.0 kg is released
from rest at the top of a frictionless incline of height 3
m and length 5 m. Taking g = 10 m/s2, use
energy considerations to find the velocity of the object at
the bottom of the incline.
(b) Repeat when µk between the object and
the plane is 1/4.
Solution:
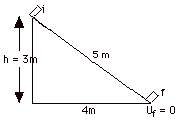
(a) Since the incline is frictionless and
no other nonconservative force acts on the object, energy
is conserved. Take the initial point i at the top of the incline
and the final point f at the bottom of the incline. Let Uf
= 0. At the initial point the potential energy is mgh,
where h is the vertical height above the bottom of
the incline. The object being released from the top of the
incline means that its initial velocity vi is
zero so that Ki = 1/2 mvi2
= 0. From conservation of energy,
| Ui |
+ |
Ki |
= |
Uf |
+ |
Kf |
|
2.0 kg(10 m/s2)(3 m) |
+ |
0 |
= |
0 |
+ |
1/2(2.0 kg) vf2 |
| |
| 60 m2/s2
= vf2 |
| vf = (60)1/2m/s
= 7.7 m/s |
(b) At the bottom of the incline
Uf = 0; at top of incline Ui = mgh.
Ki = 0. With the frictional force, a non-conservative
force acting on the block, mechanical energy is not conserved.
(Fnet)y= may= m(0)
FN - mg cos Θ
= 0
FN = mg cos Θ
fk = µkFN = µk
mg cos Θ = µk
mg(4/5)
Since the distance down the plane s = 5 m and cos fk, s
= 180o, the work by friction = (fk)
s cos fk,
s
= {µk mg cos Θ}s
cos 180o
= (1/4)(2 kg)(10 m/s2)(4/5)}(5m)(-1)
= -20 J.
Work by friction = (Uf + Kf) - (Ui
+ Ki)
-20 J = (0 + 1/2 mvf’2) - (mgh
+ 0)
-20 J = 1/2(2 kg)vf’2 - (2 kg)(10
m/s2)(3 m)
-20 J = 1kg vf’2 - 60 J
60 J - 20 J = 1kg vf’2
40 J = 40 N-m = 40 kg m2/s2 =
vf’2 kg; vf’
= (40)1/2 m/s = 6.3 m/s.
- Sample problems in 107
Problem Set for Work and Energy: 14-21, 23-41.
- Scalar or Dot Product
- Definition C = A • B
= |A||B|cos
A, B
- Work = Fs cos F,s
may be written as F • s
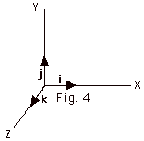
- Unit vectors
- i • i = |i||i|cos
i,
i = |1||1|cos 0o
= 1
j • j = |j||j|cos j,
j = |1||1|cos 0o
= 1
k • k = |k||k|cos k,
k = |1||1|cos 0o
= 1
- i • j = |i||j|cos
i,
j = |1||1|cos 90o
= 0 = j • i
i • k = |i||k|cos i,
k = |1||1|cos 90o
= 0 = k • i
j • k = |j||k|cos j,
k = |1||1|cos 900
= 0 = k • j
- Sample problems in 107
Problem Set for Work and Energy: 8, 22.
|
|
