|
Review - One Dimensional Motion
|
|
|
1.
|
An object moves with a constant velocity
of 15 m/s. (a) How far will it travel in 2.0 s? (b) If the
time is doubled, how far will it travel?
|
|
|
2.
|
An object, initially at rest, moves with
a constant acceleration of 10 m/s2. How far will
it travel in (a) 2.0 s and (b) 4.0 s? If this object had an
initial velocity of
4 m/s, how far will it travel in (c) 2.0 s and (d) 4.0 s?
|
|
|
3.
|
(a) An object moving with constant acceleration
changes its speed from 20 m/s to 60 m/s in 2.0 s. What is
the acceleration? (b) How far did it move in this time?
|
|
|
4.
|
An object moving with constant acceleration
along a horizontal path covers the distance between two points
60 m apart in 6.0 s. Its speed as it passes the second point
is 15 m/s. Find (a) the speed at the first point, (b) its
acceleration and (c) the distance from the point where the
object was at rest to the first point.
|
|
|
5.
|
A ball thrown straight up takes 2.0 s
to reach a height of 40 m. Find (a) its initial speed, (b)
its speed at this height, and (c) how much higher the ball
will go. Take g = 10 m/s2.
|
|
|
6.
|
A ball is thrown down vertically with
an initial speed of 20 m/s from a height of 60 m. Find (a)
its speed just before it strikes the ground and (b) how long
it takes for the ball to reach the ground. Repeat (a) and
(b) for the ball thrown directly up from the same height and
with the same initial speed.
Take g = 10 m/s2.
|
|
|
7.
|
A multiple choice question. (a) By definition,
velocity equals the change in position divided by the time
to change the position. The instantaneous velocity v = dx/dt
is (i) the slope of the position x versus time t at any instant,
(ii) the area under the x versus t curve up to that instant,
(iii) the slope of the acceleration a versus time t at any
instant. (b) Since v = dx/dt, by separation of variables dx
= v dt or ∫dx = ∫v dt. Thus the distance moved
in time t is (i) the slope of the velocity v versus time t
at any instant (ii) the area under the velocity v versus time
t curve up to time t (iii) the area under the acceleration
a versus time t curve up to time t. (c) By definition, instantaneous
acceleration a = dv/dt or (i) the slope of the position x
versus time t at any instant, (ii) the slope of the velocity
v versus time t at any instant, (ii) the area under the velocity
v versus time t curve up to time t. (d) Since a = dv/dt, by
separation of variables dv = a dt or ∫dv = ∫a
dt. Thus the change in velocity up to time t is (i) the slope
of the velocity v versus time t at any instant, (ii) the area
under the velocity v versus time t curve up to time t, (iii)
the area under the acceleration a versus time t curve up to
time t.
|
|
|
8.
|
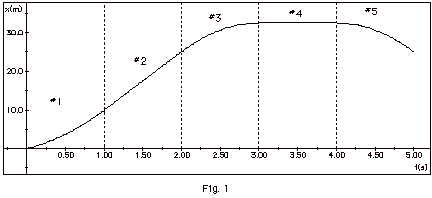
Figure 1 below is a plot of the displacement
x of an object as a function of time t. The dashed vertical
lines separate the one second intervals. During the first
time interval #1 (t = 0 to t = 1 s) of Fig. 1 decide if the
velocity of the object is (a) zero (b) constant and positive,
(c) constant and negative, (d) increasing and positive, (e)
increasing and negative, (f) decreasing and positive, or (g)
decreasing and negative. (You may use a ruler to check the
slopes of x vs t for the various time intervals.) Also decide
for the same intervals if the acceleration is (note do not
fix on one point in an interval) (h) positive (i) negative
(j) zero. Explain your answers. Repeat the above for the other
four time intervals in Figure 1.
|
|
|
9.
|
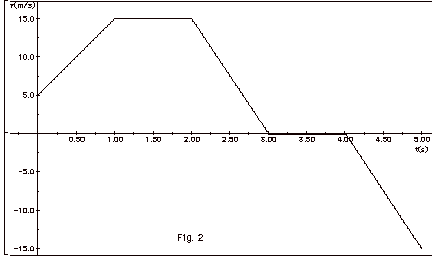
Figure 2 below shows the velocity of
a particle as a function of time. (a) Find the acceleration
for the five one-second periods and plot the acceleration
as a function of time. (b) Taking x = 0 at t = 0, find the
position of the particle at t = 0.5 s, t = 1.0 s, t = 2.0
s, t = 3.0 s, t = 4.0 s, and t = 5.0 s and plot the position
as a function of time. Look at the slopes of your x vs t curve
for the five one-second periods and show that they correspond
to the velocities of Fig. 2.
|
|
|
10.
|
An object moving with a velocity of
10 m/s is uniformly decelerated, coming to rest in a distance
of 20 m. Find (a) its deceleration and (b) the time for it
to come to rest. Plot (c) its velocity v as a function of
time t and (d) its position x as a function of t. Take xo
= 10 m.
|
|
|
11.
|
An apartment dweller sees a flower pot
(originally on a window sill above) pass the 2.0-m-high window
of her fifth floor apartment in 0.10 s. The distance between
floors is 4.0 m. From which floor did the pot fall?
|
|
|
12.
|
The acceleration of a particle is given
by a(t) = 6.0 m/s3 t. Find (a) v(t) and
(b) x(t) for a particle with vo = xo
= 0.
|
|
|
13.
|
Repeat Problem 12 for vo
= 1.0 m/s and xo = 2.0 m.
|
|
|
14.
|
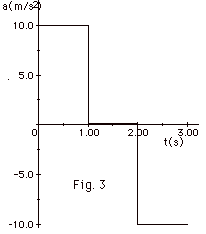
A particle starts from rest and undergoes
accelerations as plotted in Fig. 3 below for the first three
seconds. Plot a graph of (a) velocity v as a function of time
t and (b) position x as a function of time t taking xo
= 0. Find (c) the maximum velocity during the period and (d)
the distance moved by the particle in 3.0 s.
|
|
|
15.
|
At a certain instant, a ball is thrown
downward with a velocity of 8.0 m/s from a height of 40 m.
At the same instant, another ball is thrown upward from ground
level directly in line with the first ball with a velocity
of 12 m/s. Find (a) the time when the balls collide, (b) the
height at which they collide, and (c) the direction the second
ball is traveling when they collide. Take g = 10 m/s2.
|
|
|
16.
|
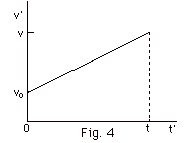
Use Fig. 4 below and geometry to find
(a) the average velocity of the particle in time t and (b)
the time at which the velocity of the particle equals the
average velocity.
|
|
|
17.
|
Sketch a graph that is a possible description
of position as a function of time for a particle that moves
along the x axis and, at t = 1 s, has (a) zero velocity and
positive acceleration; (b) zero velocity and negative acceleration;
(c) negative velocity and positive acceleration; (d) negative
velocity and negative acceleration. (e) For which of these
situations is the speed of the particle increasing at t =
1 s?
|
|