Review - Two Dimensional Motion

1.

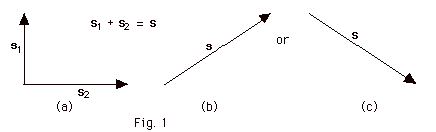
An object experiences displacements s₁ and s₂, as shown in Fig. 1a below. Is the resultant displacement s shown in Fig. 1b or Fig. 1c? Explain your answer.

2.

Show how two displacement vectors, one of magnitude 6 m and the other of magnitude 8 m, can be combined to give a resultant of (a) 2 m, (b) 14 m, and (c) 10 m.

3.

Vector A has magnitude 10 cm and makes an angle of 37^o with the x-axis. Vector B has components B_x = 8 cm and B_y = -2 cm.

Sketch the vector C = A + 1/2 B and determine its components, its magnitude, and the angle it makes with the x-axis.

4.

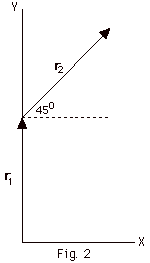
A particle moves 7.00 m along the positive Y-axis and then 7.07 m at angle of 45^o with the X-axis, as shown in Fig. 2 below. Find the resultant displacement r = r₁ + r₂ of the particle. Express r in terms of (a) unit vectors i and j and (b) its magnitude and direction.

5.

A pitcher throws a baseball with a horizontal velocity of 132 ft/s (90 mph) toward home plate that is approximately 60 ft away. What is the vertical drop of the ball when it reaches the plate? g = 32 ft/s².

6.

A young man practicing his pitching stands on a cliff and tosses a rock at a velocity of 24 m/s in a horizontal direction. At this instant a person in a car at rest in a service station 90 m from the cliff "guns" the car at a constant acceleration of 4.0 m/s² toward the cliff. The rock hits the car. (a) How long is the rock in the air? (b) How high is the cliff?

7.

A ball rolls off the edge of a 1.0 m-high table with a speed of 4.0 m/s. How far horizontally from the edge of the table does the ball strike the floor?

8.

9.

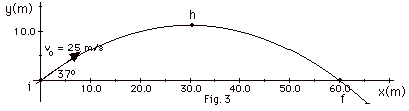
Find and draw the horizontal and vertical components of the projectile's velocity in Fig. 3 below (a) at the initial position i, (b) at the highest point h, and (c) just before it hits the ground at f. (d) Draw the velocity vector at h and f. (e) Draw the acceleration vectors for x = 20.0, 30.0 and 40.0 m.

10.

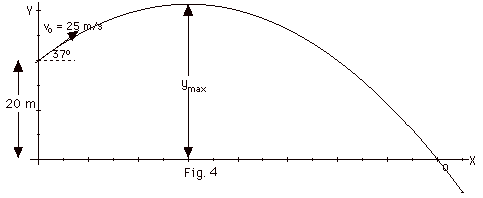
An object is shot into the air with an initial velocity v_o = 25 m/s at an angle of 37^o above the horizontal at a height of 20 m above the earth's surface (Fig. 4 below). Take g = 10 m/s². Find and draw the horizontal and vertical components of the projectile’s velocity in Fig. 4 (a) at the initial position, (b) at the highest point. Find (c) the maximum height y_max to which the object rises, (d) the time for it to return to the earth, (e) the distance moved horizontally, and (f) draw the horizontal and vertical components of the velocity just before it hits the ground. (g) Draw the velocity vector just before it hits the ground and find its magnitude and direction.

11.

For the projectile of Fig. 4 above, write numerical expressions for:

(a) the initial position vector r_o = x_oi + y_oj,

(b) the initial velocity vector v_o = v_oxi + v_oyj,

(c) the acceleration vector a = -a_yj,

(d) the velocity at any time t vector v(t) = v_xi + v_yj,

     and show that:

(e) v(t) = v_o + at,

(f) the position vector as a function of time r(t) = xi + yj,   and

(g) r(t) = r_o + v_ot + 1/2 at².

12.

A boy throws a ball into the air as hard as he can and then runs as fast as he can under the ball in order to catch it. If his maximum speed in throwing the ball is 20 m/s and his best time for a 20-m dash is 3.0 s, how high does the ball rise? Take g = 10 m/s².

13.

A driven golf ball just clears the top of a tree that is 15 m high and is 30 m from the tee, and then lands (with no roll or bounce) on the green, 180 m from the tee. What was the initial velocity imparted to the golf ball? Take g = 10 m/s².

14.

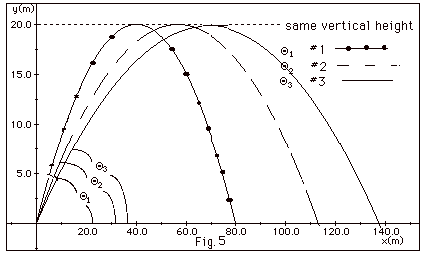
Projectiles in Fig. 5 below are shot off at different angles with Θ₁ (path designated –•–•–•–•–) greater than Θ₂ (path designated with __ __) greater than Θ₃ (path designated _____ ), but the maximum vertical height reached by each projectile is the same. (a) If t₁ represents the time for the object to reach the ground when projected at angle Θ₁, t₂ the time to reach the ground when launched at angle Θ_2, and t₃ for the one at angle Θ_3, find whether (i) t₁ > t₂ > t₃, (ii) t₃ > t₂ > t_1, or (iii) t₁ = t₂ = t₃. (b) The initial velocity for path #1 is (i) greater than the initial velocity for path #2 which is greater than the initial velocity for path #3, (ii) less than the initial velocity for path #2 which is less than the initial velocity for path #3, (iii) is the same as the initial velocity for path #2 and path #3. (c) Are your answers to (a) and (b) consistent with the fact that the range for path #3 is the greatest? Explain your answers.

15.

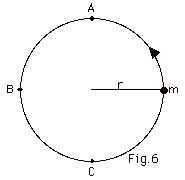
A small object of mass m rotates counterclockwise on a horizontal frictionless plane at the end of a string of length r = 0.4 m with constant speed v = 2.0 m/s. On Fig. 6 below draw the magnitude and direction of (a) the velocity and (b) the centripetal acceleration at points A, B, and C. (c) Are the velocity and the acceleration constant? (d) Could you use this method to find how an object would withstand a number of "g's"?  Explain your answers.

16.

(a) The period T of an object moving with uniform circular motion is defined as the time for one complete rotation. Find the period for the particle in #15. (b) The frequency f of an object is defined as the number of rotations it makes per second. Find the frequency of the particle in #15. How is the frequency related to the period? Write an expression for the centripetal acceleration in terms of (c) π, r, and T, (d) π, r, and f.

17.

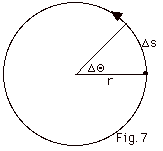
An angle in radians is defined as the arc an angle subtends divided by the radius of the circle. (a) In Fig. 7 below, what does the angle ΔΘ equal? (b) The magnitude of the angular velocity of the particle ω is defined as the limit of ΔΘ/ Δt as Δt approaches zero. Find ω. (c) The direction of ωis found by curling the fingers of your right hand in the direction of motion. Your thumb then points in the direction of the motion. What is the direction of ω? (d) Is uniform circular motion a case of constant angular velocity?

18.

In time t, an object moving with constant angular velocity ωrotates through angle Θ= ωt. Find (a) r(t) in unit vector notation, (b) v(t) in unit vector notation, (c) v_x, v_y and v, (d) a(t) in unit vector notation, (e) a_x, a_y, and a. (f) Draw the vectors v and a and their components on Fig. 8 below.

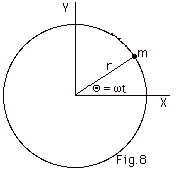
19.

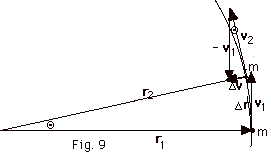
Figure 9 below represents an object moving in a circle with uniform circular motion. In this type of motion, the magnitude of the velocity v remains constant, but its direction is always tangent to the path. The direction continuously changes. Uniform circular motion is an example of constant speed, but not of constant velocity. That is v₁ = v₂, but v₁ is not equal to v₂. The object of mass m is located on the circle initially by the position vector r₁ with its instantaneous velocity v₁ tangent to the circle or perpendicular to r₁. Later the velocity v₂ is perpendicular to the position vector r₂. The displacement vector Δr = r₂ – r₁. In Fig. 9, the negative of the position vector r₁ has been added to r₂ to give r₂ – r₁ = Δr.

(a) Use the triangle with r₂, r₁, Δr and the triangle with v₂, v₁, Δv to find an expression for Δr/r and Δv/v. Recall that r₂ = r₁ and v₂ = v₁. Now find an expression for the acceleration from a = lim Δt 0 of Δv/ Δt.

(b) Find the direction of the acceleration from a = lim Δt 0 of Dv/ Δt.