Review - Angular Motion

1.

Write an expression for (a) the distance x moved by a particle traveling with a constant linear velocity v in time t and (b) the angle Θ moved by a particle rotating with a constant angular velocity ω in time t.

2.

Write an expression for (a) the constant linear acceleration a of a particle going from linear velocity v_o at time t = 0 to a velocity v at time t and (b) the constant angular acceleration going from angular velocity ω_o at time t = 0 to angular velocity ω at time t.

3.

Given that (a) dx/dt = v and a is constant, find x(t) for an object initially at x_o traveling with v_o at  t = 0 and (b) dΘ/dt = ω and αis constant, find Θ(t) for an object initially at Θ_o and rotating with ω_o at  t = 0.

4.

Starting from Θ_o= 0 and ω_o = π s^-1, a wheel is given a constant angular acceleration of 4 π s^-2.   After 4.0 s find (a) its angular speed and (b) how many turns the wheel has made.

5.

The angular position of a particle is given by Θ(t) = b + ct + et², where b, c, and e are constants.  At time t₁, the radial displacement of the particle is r.  Find (a) the angular velocity, (b) the angular acceleration α, (c) the linear velocity, (d) the tangential acceleration, and (e) the centripetal acceleration of the particle at time  t = t₁.

6.

Show that the direction, as well as the magnitude of (a) the tangential velocity of a particle moving in a circle of radius r drawn from the center of the circle and rotating with angular velocity ω  is v = ω x r and (b) the particle's radial or centripetal acceleration is a = ω  x (w x r).

7.

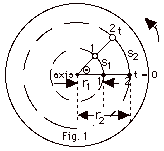
The wheel shown in Fig. 1 below rotates with constant angular velocity ω. Show that points 1 and 2 on the wheel move with the same angular velocity, but different linear velocities. In Fig. 1, the initial positions of the two points are shown by dark circles and the positions at time t are shown with open circles. Point 1 is a distance r₁ from the axis and Point 2 is a distance r₂ > r₁ from the axis.

8.

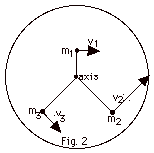
Some of the particles that make up the rigid body of a disk are shown in Fig. 2 below. (a) Write a summation for the total kinetic energy of the disk with particles from i = 1 to i = N in terms of the mass m_i of a particle and its velocity v_i. (b) Substitute the expression for the angular velocity ω of the disk in terms of v_i and r_i. (c) Take the 1/2 and ω out of the summation and identify the quantity represented by the summation. (d) Rewrite the kinetic energy in terms of 1/2,  ω, and the quantity represented by the summation.

9.

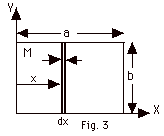
Calculate the moment of inertia about the Y-axis for a uniform plate of dimensions a x b with mass M when the Y-axis coincides with an edge of the plate along the b dimension, as shown in Fig. 3 below.

10.

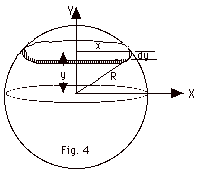
Determine the moment of inertia of a uniform solid sphere with radius R, mass M, and density ρ= M/(4πR³/3), about an axis through its center.  Hint: Divide the solid sphere into disks of thickness dy and radius x, as shown in Fig. 4 below. Use the rotational inertia of a disk to find the differential moment of inertia for the disk dI = 1/2 x² dm.

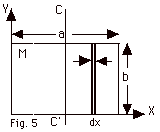
11.

(a) Look at Fig. 3 above and Fig. 5 below and decide whether the moment of inertia of the thin plate is greater about the Y-axis or about the CC’ axis of Fig. 5. (b) Calculate the moment of inertia by integration. (c) Use the parallel axis theorem to determine the moment of inertia about the CC’ axis.

12.

Find (a) A x B when A = A_xi + A_yj and B = B_xi + B_yj and (b) the angle between A and B.

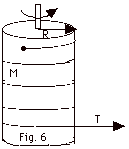
13.

A massless string is wrapped around a uniform solid cylinder with mass M = 30 kg and radius R = 0.040 m. One end of the string is attached to the cylinder and the free end is pulled tangentially by a force that maintains a constant tension T = 3.0 N (Fig. 6 below).  Find (a) the angular acceleration and (b) the angular speed of the cylinder 2.0 s after the force is applied to the cylinder initially at rest.

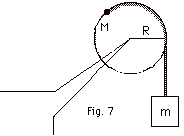
14.

A massless string is wrapped around a disk that has a radius R = 0.100 m and a mass M = 1.00 kg. The free end of the string is attached to a hanging 0.500-kg block; the other end is fixed to a point on the rim of the disk (Fig. 7). Neglecting friction, find (a) the linear acceleration of the hanging block and (b) the force exerted by the bearing on the pulley. Take g = 10 m/s².

15.

Show that the magnitude of the torque τ equals the product of (a) the force F times the component of the distance r from the axis perpendicular to the force F and (b) r and the component of F perpendicular to r.

16.

A uniform rod of length L and mass M is free to rotate about a frictionless pivot at the end attached to the wall. The pivot is shown as a dark circle in Fig. 8 below. The rod is released from rest in the horizontal position. Find the initial (a) angular acceleration of the rod and (b) the linear acceleration of the right end of the rod.

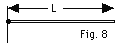
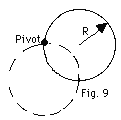
17.

A uniform solid disk of radius R and mass M is free to rotate on a frictionless pivot through a point on its rim, as shown in Fig. 9 below. (a) If the disk is released from rest in the position shown by the solid circle, what is the velocity of the center of mass when it reaches the position shown by the dashed circle? (b) What is the speed of the lowest point on the disk in the dashed position? (c) Repeat (a) and (b) for a uniform hoop.

18.

A solid disk of mass m is rolling along a surface. Its center has velocity v.  What is the kinetic energy of the disk?

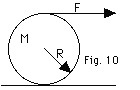
19.

A spool of wire of mass M and radius R is unwound under a constant force F, as shown in Fig. 10 below. Find (a) the acceleration of the center of mass and (b) the force of friction.

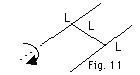
20.

A rigid body is made of three identical thin rods, each with length L, fastened together in the form of a letter H (Fig. 11 below). The body is free to rotate about a horizontal axis that runs along the length of one of the legs of the H. The body is released from rest in a position where the plane of the H is horizontal. What is the angular speed of the body when the plane of the H is vertical?

21.

A sphere of radius R rolls down an inclined plane of height h and angle of inclination.  Find (a) using conservation of energy, the velocity of the center of mass when the sphere is at the bottom of the incline and (b) using F_net = ma and τ_net = Iα, (i) the acceleration of the center of mass, (ii) the frictional force that acts on the sphere, and (iii) the speed of the sphere at the bottom of the incline.

22.

A pencil of length L, initially standing on end falls over. With what speed does the eraser strike the horizontal surface, assuming the pencil point remains at rest on the surface?

23.

A solid cylinder of mass M and radius R rolls without slipping on a rough horizontal surface and is accelerated to the right by a constant force F applied at the cylinder's symmetry axis. Find (a) the acceleration of the cylinder and (b) the force of friction on the cylinder.

24.

A uniform solid sphere with a mass M = 2.0 kg and a radius R = 0.10 m is set into motion with an angular speed ω_o = 70 rad/s.  At  t = 0 the sphere is dropped a short distance (without bouncing) onto a horizontal surface. There is friction between the sphere and the surface. Find (a) the angular speed of rotation when the sphere finally rolls without slipping at time  t = T and (b) the amount of kinetic energy lost by the sphere between  t = 0 and  t = T. (c) Show that the result in (b) equals the work done against the frictional force that acts to cause the sphere to roll without slipping.

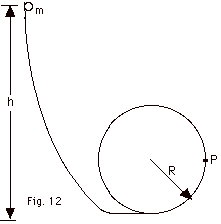
25.

A small solid sphere of mass m and radius r rolls without slipping along the loop-the-loop shown in Fig. 12 below. Find (a) the minimum height h above the bottom of the track you must release the sphere so that it will not leave the track at the top of the hoop (assume the radius of the loop-the-loop R >> r) and (b) the force of the track on the sphere at P in Fig. 12 when it is released from the height h found in (a).

26.

A particle of mass m moves in the xy plane in a circular path of radius r. The motion of the particle is counter-clockwise. Find (a) the magnitude and direction of its angular momentum relative to the center of the circle when its velocity is v and (b) an alternative expression for L in terms of the angular velocity ω.

27.

Show that the magnitude of the angular momentum of a particle can be written as the product of (a) the momentum of the particle p and the component of its position vector r perpendicular to p and (b) r and the component of its momentum p perpendicular to r.

28.

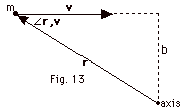
Find the direction and magnitude of the angular momentum of the particle of mass m moving with velocity v a distance r from the axis shown in Fig. 13 below.

29.

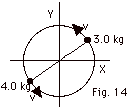
A light rod 1.0 m in length rotates in the xy plane about a pivot through the rod's center. Two particles of mass 4.0 kg and 3.0 kg are connected to its ends (Fig. 14 below). Determine the angular momentum of the system about the origin at the instant the speed of each is 5.0 m/s.

30.

Show dL/dt of a particle equals the torque τ acting on it.

31.

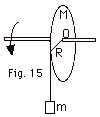
A mass m is attached to a light cord, which is wound around a pulley (Fig. 15 below). The pulley is a uniform disk of mass M and radius R. Find (a) the net torque on the system about the point O, (b) the angular momentum of the system when the mass m has a speed v, and (c) the acceleration of m using
dL/dt =τ.

32.

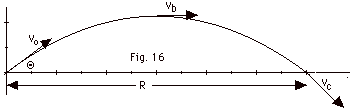
A particle is launched with a velocity v_o at an angle of Θ with the horizontal as shown in Fig. 16 below. Find the angular momentum of the particle about the origin when the particle is (a) at the origin, (b) at its highest point, and (c) just before it hits the ground. (d) What is the direction of the change in angular momentum and what torques produces this change?

33.

A particle of mass m and speed v_o collides with and sticks to the edge of a uniform solid disk of mass M and radius R. If the disk is initially at rest and pivoted about a frictionless axle through the center of the disk, find (a) the angular velocity of the system after the collision and (b) the loss of kinetic energy in the collision.

34.

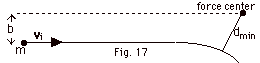
A small particle of mass m moves with velocity v_o when it is a great distance from a very large mass object that repels it. The potential energy of the system is A/r, where A is a positive constant and r is the distance between the two objects. Use conservation of energy and angular momentum to find the minimum distance d_min  between the particle and the large mass (Fig. 17 below) in terms of A, m, b, and v_i.

35.

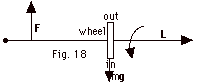
You exert a force F on the axle of a spinning wheel (Fig. 18 below) to lift it. If the wheel is spinning clockwise as you look at it, what happens to the wheel. Explain your answer.

36.

Show only the direction of L changes when τ  is perpendicular to L.

37.

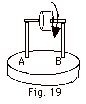
A wheel of mass m and moment of inertia I relative to its axis is spinning with an angular velocity ω while the ends of the axle are supported by two posts A and B, separated by a distance 2d and mounted on a rotatable platform (Fig. 19 below). At what angular velocity (direction and magnitude) must the platform be turned so that post B can be removed and the spinning wheel still maintain a fixed position relative to the platform?

38.

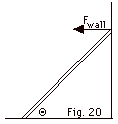
A uniform ladder of length L and weight W = 50 N rests against a smooth, vertical wall. The smoothness of the wall means that the force due to the wall is horizontal and to the right, as shown in Fig. 20 below. If the coefficient of static friction between the ladder and ground is µ_s = 0.40,  find the minimum angle Θ_min  such that the ladder will not slip.

39.

Solve Problem 24 above using conservation of angular momentum.

40.

Two balls of mass M equal to 0.975 kg are attached to the ends of a thin rod of negligible mass which is 1.00-m long. The rod is free to rotate about a vertical axis through it center. While the rod is horizontal (Fig. 22 below), a putty glob of mass m = 0.050 kg drops onto one of the balls with a speed of 3.00 m/s and sticks to it. Find (a) the angular speed of the system just after the putty glob hits and (b) the angle through which the system rotates until it momentarily stops. You may treat all the masses as point particles. Take g = 10 m/s².