Review - Center of Mass, Momentum, and Collisions

1.

A tennis player receives a shot with the ball (0.060 kg) traveling horizontally at 50 m/s, and returns the shot with the ball traveling horizontally as 40 m/s in the opposite direction. What is the impulse delivered to the ball by the racket?

2.

Four particles are distributed in the X-Y plane as shown in Fig. 1 below. Find the coordinates (X_CM, Y_CM) of the particles. The particles are on the corners of a
2.0-m square.

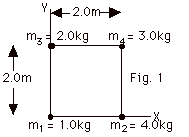
3.

A 1500-kg automobile travels eastward at a speed of 8.0 m/s. It makes a 90^o turn to the north in a time of 3.0 s and continues with the same speed. Find (a) the impulse delivered to the car as a result of the turn (b) the average force exerted on the car during the turn and (c) the average force of the car on the road during the turn.

4.

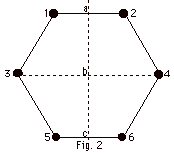
Six particles with equal mass m are arranged to correspond to the six corners of a regular hexagon, as shown in Fig. 2 below. Locate the center of mass of the system.

5.

Object A of mass 1.0 kg travels with a speed of 4.0 m/s, while object B of mass 2.0 kg travels with a speed of 2.00 m/s. Compare (a) the magnitude of their momenta and (b) their kinetic energies.

6.

Two skaters stand in the center of a circular rink of frictionless ice. When the skaters push on one another, they move apart along the same straight line. If the skater of mass m₁ = 50 kg reaches the edge of the rink after 12 s and the other skater reaches the opposite edge of the rink in 18 s, what is the mass m₂ of the second skater?

7.

A 0.050-kg block moving to the right with a speed of 0.20 m/s collides with a 0.10-kg block moving to the left with a speed of 0.04 m/s. After the collision the blocks stick together and go off with a common velocity v_f. Find v_f.

8.

For a number of point masses, the x-component of the center of mass is:

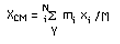
and for an extended object,



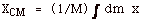
An object of mass M is in the shape of a right triangle with altitude a and base b as shown in Fig. 3 below. Find (a) the area of the triangle, (b) the mass per unit area σ. (c) the area dA of the element in Fig. 3a of height dy and width dx, (d) the mass dm of this element, (e) x dm, (f) the equation for the line which is the hypotenuse of the triangle, (g) an expression for x dm in terms of x and constants, (h) the integral expression for X_CM with limits and X_CM.  Repeat using Fig. 3b for Y_CM.

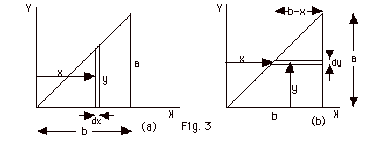
9.

Find the position of the center of mass of five equal-mass particles located at the five corners of a square based right pyramid with sides of length L and height h.

10.

A 75-kg man is standing in a 225-kg barge and is originally 10 m from a pier on a still lake. The man walks towards the pier a distance of 2.0 m relative to the barge, and then stops. Assuming the barge can move through the water without resistance, how far is the man now from the pier?

11.

After a nucleus decays, the products of the decay move off in opposite directions with equal and opposite momenta. What is the initial momentum of the nucleus?

12.

Object A with mass m_A = 3.0 kg moving in the +x-direction with a velocity of
1.0 m/s collides with object B with m_B = 2.0 kg moving in the +y-direction with velocity of 2.0 m/s.  After the collision, the blocks stick together. Find the magnitude and direction of the final velocity v_f.

13.

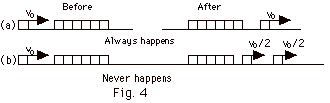
Seven steel blocks of equal mass m rest on a frictionless table. If one of the blocks is given an initial velocity v_o and it collides with the other six, a block at the other end always goes off with v_o (Fig. 4a below). The collision in Fig. 4b below never happens. Suggest a reason why the collision in Fig. 4b never happens.

14.

This is a one-dimensional problem. A 1.0-kg block moving with a velocity of
2.0 m/s to the right collides elastically with a second block that is initially at rest. Find the velocities of the two blocks after the collision if the mass of the second block is (a) 1.0 kg, (b) 1,000 kg, (c) 0.001 kg.

15.

This is a one-dimensional problem. A 4.0-kg block moving with a velocity of
2.0 m/s to the right collides elastically with a 1.0-kg block moving with a velocity of 3.0 m/s to the left. Find the velocity of the two blocks after the collision.

16.

Describe the collision of the blocks in Problem 15 in the center of mass coordinate system.

17.

A disk with a mass m₁ = 10 kg traveling along a smooth surface with a velocity of 24 m/s along the +X-axis collides with a stationary second disk of mass m₂ = 20 kg. After the collision, the first disk moves along the + Y-axis with a velocity of 10 m/s. What was the velocity (direction and magnitude) of the second disk after the collision?

18.

A disk with a mass m₁ = 2.0 kg traveling along a smooth surface with a velocity of 39 m/s along the +X-axis collides with a stationary second disk of mass m₂ = 8.0 kg. After the collision the second disk moves with a velocity of 10 m/s at an angle of 37^o above the X-axis. (a) Find the velocity (magnitude and direction) of the first disk after the collision. (b) Was this an elastic collision?

19.

A proton moving with a velocity of v_1i i collides elastically with another proton initially at rest. If both protons have the same speed (v_1f = v_2f) after the collision, find (a) the speed of each proton after the collision in terms of v_1i and (b) the direction of the velocity vectors after the collision.

20.

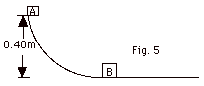
A 2.0-kg Block A slides down a frictionless chute (Fig. 5 below) and then strikes a stationary 9.2-kg block B on a horizontal table. (a) What is the velocity of A at the bottom of the chute? (b) If A sticks to B after the collision, what is their common velocity immediately after the collision? (c) If the frictional force between the blocks and the table is 2.8 N, how far do they slide before coming to rest? Take g = 9.8 m/s².

21.

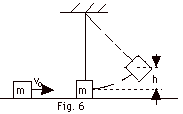
A mass m hangs by a string of length L.  A second identical mass is sliding along a frictionless surface with velocity v_o (Fig. 6 below). (a) If the two masses have an elastic collision, how high will the first mass rise? (b) If the two masses have a totally inelastic collision, how high will the masses rise?

22.

A horizontal force of 0.80 N is required to move m₂ = 5.0 kg of Fig. 7 below across the surface with a constant velocity. With the block initially at rest, a 0.020-kg bullet m₁ fired horizontally into the block causes the block (with bullet inside) to slide 1.5 m before coming to rest again. Find the speed v_o1 of the bullet.

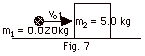
23.

A 2.0-kg steel ball A and a 3.0-kg steel ball B coated with putty are suspended by strings of length L = 0.80 m. When ball A is released from the position shown in Fig. 8 below, it strikes ball B. After the collision, the balls move with a common velocity. Find (a) the kinetic energy of ball A just before the collision, (b) the velocity of ball A just before the collision, (c) the common velocity of the balls immediately after the collision, and (d) the height to which the two balls rise after the collision. Take g = 10 m/s².

24.

Now imagine the putty of ball B in #23 is removed and there is an elastic collision between the two balls. Find (a) the kinetic energy of ball A just before the collision, (b) the velocity of ball A just before the collision, (c) the velocities of A and B immediately after the collision, and (d) the heights to which ball (i) B and (ii) A rise after the collision.

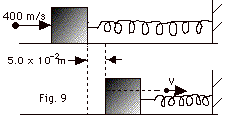
25.

A 5.0 x 10^-3-kg bullet moving with an initial speed of 400 m/s is fired into and passes through a 1.0-kg block, as shown in Fig. 9 below. The block initially at rest on a frictionless, horizontal surface is connected to a spring of force constant 900 N/m. If the block moves a distance of 5.0 x 10^-2 m to the right after impact and comes to rest momentarily, find (a) the speed at which the bullet emerges from the block and (b) the energy lost in the block.

26.

A number of years ago, The New Yorker gave the following quote, "Every time you drop a pin, the earth moves upward slightly." The comment after that was, "Butterfingers." Please explain the quote.