|
|
|
1.
|
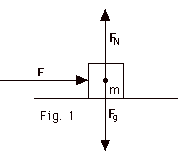
An object of mass m, resting on a horizontal
frictionless surface, is acted upon by an applied force F,
the normal force of the surface FN, and
the gravitational attraction of the earth Fg,
as shown in Fig. 1 below. Find (a) Fg, (b) FN
and the acceleration of the object when (c) F = 12 N and m
= 2.0 kg, (d) F = 24 N and m = 2.0 kg, (e) F = 12 N and m
= 1.0 kg. Take g = 10 m/s2.
|
|
|
2.
|
In Fig. 1 above, the surface now exerts
a frictional force of 4.0 N on the object when it is in motion.
If the mass of the object m = 2 kg, find the acceleration
of the object when (a) F = 12 N and (b) F = 24 N.
|
|
|
3.
|
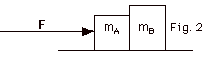
Two objects of mass mA = 2.0
kg and mB = 4.0 kg rests on a frictionless
surface (Fig. 2 below). An applied force F = 12 N acts on
object A, as shown in Fig. 2. Find (a) the acceleration of
the objects, (b) the force FAB of object B on A
and (c) the force FBA of object A on B.
|
|
|
4.
|
The two objects in Fig. 2 above are now
connected by a massless string, string 1, and pulled
to the right by exerting a force of 12 N to the right through
another massless string. Find (a) the acceleration of the
blocks and (b) the tension in string 1.
|
|
|
5.
|
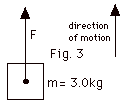
(a) An object of mass m = 3.0 kg is set
into motion and then raised with a constant velocity of 3.0
m/s. What applied force F is needed? (b) The object is now
given an acceleration of 3.0 m/s2. Now what applied
force is needed?
Take g = 10 m/s2. See Fig. 3 below.
|
|
|
6.
|
A system, consisting of a wide rope of
mass 0.10 kg between two blocks each of mass 0.10 kg, is lifted
by an applied force F = 9.0 N (Fig. 4 below). (a) Find the
acceleration of the system. Find the tension at (b) the top
of the rope, and (c) the bottom of one-fifth of the rope.
Take g = 10 m/s2.
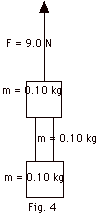
|
|
|
7.
|
A block of mass m = 2.0 kg is moved to
the right on a horizontal surface by a force of 26 N. The
coefficient of kinetic friction µk between
the surface and the object is 1/5. (a) Draw the object and
show all of the forces acting on it. Find (b) the frictional
force on the block and (c) the acceleration of the block.
Take g = 10 m/s2.
|
|
|
8.
|
Repeat Problem 7 when the applied force
makes an angle of 22.6o above the horizontal.
|
|
|
9.
|
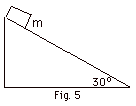
An object of mass m = 3.0 kg accelerates
down the frictionless inclined plane of Fig. 5 below. (a)
Show all the forces acting on the object. Draw a X-axis parallel
and down the plane and a Y-axis perpendicular to the plane
and upward. (b) Find and draw the components of the forces
on the X and Y-axes. (c) Find the acceleration of the block.
Take g = 10 m/s2.
|
|
|
10.
|
Repeat Problem 9 for a coefficient of
kinetic friction µk between the surface and
the object of 0.154.
|
|
|
11.
|
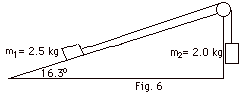
The coefficient of kinetic friction between
the block of mass m1 = 2.5 kg and the plane in
Fig. 6 below is 1/6. Find (a) the acceleration of the block
and (b) the tension in the string. Take g = 10 m/s2.
|
|
|
12.
|
An object of mass m = 2 kg moves in a
circle on a table with uniform circular motion. The speed
of the object is 2 m/s and the radius of the circle is 0.5
m. Find the (a) frictional force acting on the object and
(b) total force of the table on the object.
|
|
|
13.
|
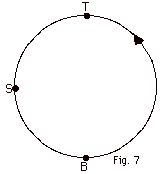
A wooden rod of negligible mass is connected
to the shaft of a motor. An object with mass m = 2 kg is attached
to the other end of the rod. As the shaft rotates, the object
moves in a vertical circle of radius 0.5 m with a constant
speed of magnitude v = 3 m/s. (a) Find the magnitude of the
centripetal acceleration for this object. The vertical circular
path is shown in Fig. 7 below for an object that moves counterclockwise.
Redraw the figure and show on it, the direction of the velocity
at (b) B, the bottom of the circle, (c) T, the top of the
circle and (d) S, the side of the circle. Now draw the direction
of the acceleration for points (e) B, (f) T and (g) S. Find
the force of the rod on the object For for
points (h) B, (i) T and (j) S.
|
|
|
14.
|
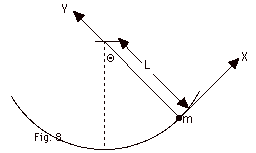
A simple pendulum consists of a point
object (called a bob) of mass m at the end of a massless string
of length L. When the string is vertical, the bob is at its
equilibrium position. When it goes to the right a restoring
force tends to return it to the equilibrium position. When
it goes to the left, the restoring force again tends to return
it to the equilibrium position. (a) Isolate the object and
show all the forces that act on it. (b) Taking the X-axis
tangent to the path and the Y-axis in toward the center of
the arc (Fig. 8 below), write equations for (Fnet)x
= max and (Fnet)y = max,
with the correct forces or a component of a force under (Fnet)x
and (Fnet)y. Find (c) ax
and the tension in the string when the bob is (i) at its maximum
displacement and (ii) the equilibrium position.
|
|
|
15.
|
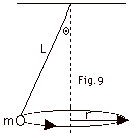
A small object of mass m is suspended
from a string of length L. The object revolves in a horizontal
circle of radius r with constant speed v, as in Fig. 9 below.
Since the string sweeps out the surface of a cone, the system
is called a conical pendulum. (a) Choose a X-axis and Y-axis
for the figure and draw all of the forces acting on the object.
(b) Write equations for (Fnet)x = max
and (Fnet)y = max. Find (c)
the speed of the object and (d) the period of revolution T.
|
|
|
16.
|
A piece of string of length L, which
can support a maximum tension T, is used to whirl a particle
of mass m in a circular path. What is the maximum speed with
which the particle may be whirled if the circle is (a) horizontal
as in Fig. 9 above or (b) vertical?
|
|
|
17.
|
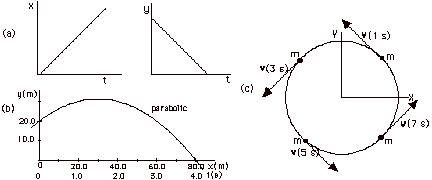
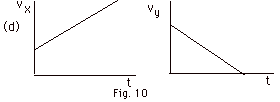
The graphs shown in Fig. 10 below give
information regarding the motion in the xy plane of four different
particles. For each case, write equations that describe the
force components Fx and Fy.
|
|
|
18.
|
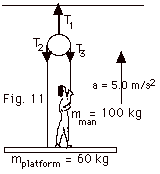
A man is raising himself and the platform
that he stands on with an acceleration of 5.0 m/s2
by means of the rope-and-pulley system shown in Fig. 11 below.
The man's mass is 100 kg and the platform's is 60 kg. Assume
the pulley and rope are massless and neglect any tilting effects
of the platform. (a) Find the tension in rope 1. With
our assumptions, T2 = T3 = T1/2.
(b) Draw separate force diagrams for the man and for the platform,
label and identify each force acting on them. (c) Find the
force of contact exerted by the platform on the man. Take g = 10 m/s2.
|
|
|
19.
|
Two blocks of mass m1 = 2.0
kg and m2 = 4.0 kg are pushed by an external force
F = 45 N, as shown in Fig. 12 below. The coefficient of kinetic
friction µk between the surface and m2
is 0.25. Find the minimum value of the coefficient of static
friction µs between m2 and m1
that will prevent m1 from slipping on m2.
Hint: First isolate the entire system, and then the blocks
individually. Take g = 10 m/s2 .
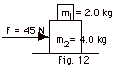
|
|
|
20.
|
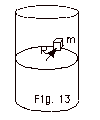
A block with a mass m will be "pinned
by static friction" against the wall of a cylindrical
shell that rotates about a vertical axis when it exceeds a
certain critical frequency value fo. (a) Isolate
the block and show all the horizontal and vertical forces
acting on it. (b) Show that fo = (1/2 π)(g/µsR)1/2,
where µs is the coefficient of static
friction between the block and the wall of the cylinder and
R is its radius (Fig. 13 below).
|
|
|
21.
|
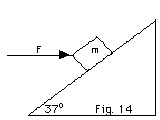
A block with a mass m = 2.0 kg initially
at rest is pushed up the incline of 37o by a horizontal
force F = 60 N (Fig. 14 below). The coefficient of kinetic
friction between the block and the incline µk
=1/2. Find the acceleration of the block.
|
|
|
22.
|
A man of mass 60-kg pushes on a sled
of mass 10-kg and the man and the sled accelerate forward
with an acceleration of 2.0 m/s2. Neglect a frictional
force on the sled and find (a) the force of the man on the
sled, (b) the force of the sled on the man and (c) the frictional
force of the snow on the man.
|
|
|
23.
|
A 10-kg object rests on a scale in an
elevator. Find the reading on the scale when the elevator
moves up with (a) a constant velocity of 5 m/s and (b) a constant
acceleration of 5 m/s2. Take g = 10 m/s2.
|
|
|
24.
|
Two spheres of identical radii, one of
lead, the other of wood fall from rest in air from a certain
height. Assume the frictional force of the air is the same
on both. Do the spheres have the same acceleration?
|
|