Review - Wave Motion

1.

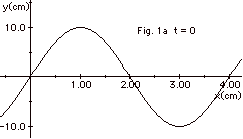
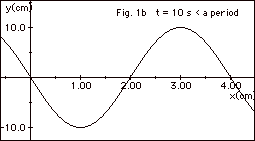
Figure 1a below represents a wave at  t = 0 traveling along a rope to the right. Figure 1b below represents the same wave at  t = 10 s = a fraction of the period T.  Find (a) the wavelength of the wave, (b) the frequency of the source that produces the wave, (c) the velocity of the wave, (d) on an extension of the graph to the right, two other positions where you expect to find crests at
t = 10 s, (e) at what later time there will be another crest at x = 1 cm.  (f) the number of times the displacement of the rope is zero at x = 2.0 cm during each period, and (g) the number of crests that pass x = 1.0 cm in 80 s.

2.

For the wave of Fig. 1, sketch a graph of the displacement y as a function of time t for (a) x = 0, (b) x = 2.0 cm and (c) x = 4.0 cm from t = 0 to t = 20 s.

3.

(a) In Fig. 1, is the point at x = 0 in phase with the point at x = 2.0 cm? (b) Is it in phase with the point at x = 4.0 cm?

4.

Write an equation for the wave of Fig. 1 that gives the displacement y as a function of x and t.

5.

Write an equation for y as a function of t for the point at (a) x = 0 , (b) x = 2.0 cm and (c) x = 4.0 cm for the wave of Fig. 1.

6.

For x = 0, write an equation for the transverse (a) velocity and (b) acceleration as a function of time for the wave of Fig. 1.

7.

Illustrate, by drawing figures, (a) two waves of the same amplitude but different wavelengths, and (b) two waves of the same wavelength but different amplitudes.

8.

At  t = 0  a wave traveling along a rope to the right has a maximum displacement of +10 cm at x = 0. The source that produces the wave makes 10 vibrations per second. The velocity of the wave is 40 cm/s. Sketch the displacement y of the rope as a function of the distance x along the rope for (a) t = 0 and (b) t = 0.05 s. (c) Write an equation for y as a function of x and t for this wave.

9.

The equation of a transverse traveling wave on a string is y(x,t) =
2.0cm sin(0.50 π cm^-1x - 200 π s^-1 t) (a) Find the amplitude, wavelength, period, frequency, velocity, and the direction of motion of the wave. (b) Sketch the wave at the following values of t: 0, 0.0025 s, and 0.0050 s. (c) Find the transverse velocity of the string at x = 1.0 cm at t = 0 and t = 0.0025 s.

10.

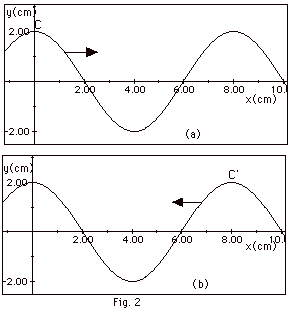
Fig. 2a below represents a wave at time t = 0 traveling along a rope to the right and Fig. 2b below a wave along the same rope to the left, which together produce a standing wave. (a) How far apart will crest C and crest C’  be at t = T/2, where T = the period? (b) Describe the resultant displacement of the rope as a function of x at t = 3T/4.

11.

Do points on a rope along which (a) a traveling wave exists, (b) a standing wave exists, vibrate up and down with simple harmonic motion? Do points on a rope along which (c) a traveling wave exists, (d) a standing wave exists, have the same amplitude? (c) How many times in one period will the entire rope have zero displacement for (e) a traveling wave? (f) a standing wave?

12.

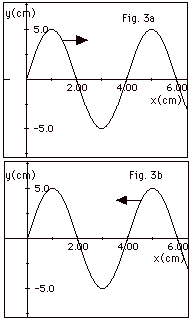
A wave travels along a rope to the right in the +x-direction (there is no reflected wave).  At time t = 0, a plot of displacement y as a function of distance x along the rope looks like Fig. 3a below. Sketch a graph of displacement y as a function of x for t = -T/4,  t = T/4,  and t = T/2, where T is the period of the wave.

13.

Sketch a graph of the displacement y of the rope for the wave of Problem 12 at x = 0, as a function of time for the times given in #12.

14.

A wave travels along a rope to the left in the -x-direction (there is no reflected wave).  At time t = 0, a plot of displacement y as a function of the distance x along the rope looks like Fig. 3b above. Sketch a graph of displacement y as a function of x for the times given in #12.

15.

We now look at the rope for different times due to the combined displacements by the waves of Fig. 3a and Fig. 3b below.  At time t = 0,  a plot of the resultant displacement y due to both waves versus position x looks like Fig. 3c below. Sketch a graph of displacement y as a function of x for the times given in #12.

16.

Sketch a graph of the displacement of the rope as a function of time at x = 1.0 cm in Fig. 3c above.

17.

The velocity of a wave along a string depends only on the tension or force F exerted on the string and the mass per unit length µ of the string. (a) From a consideration of the units of the following quantities, a dimensional analysis, decide which is the correct expression for a wave along a string: (i) µ /F,
(ii) F/ µ ,  (iii) ( µ /F)^1/2,  or (iv) (F/ µ )^1/2.  (b) Standing waves are set up in a string by a vibrator of frequency f.  If the tension in the string is increased by a factor of four, what happens to the number of nodal points?

18.

19.

A stretched string has a mass per unit length of 4.0 x 10^-3 kg/m and a tension of 1.6 N.  A sinusoidal wave on this string has an amplitude of 1.0 cm and a frequency of 100 Hz and is traveling toward decreasing x. Write an equation for this wave.

20.

A certain violin string is 50 cm long between its fixed points. The string produces a note of A (440 Hz) when played without fingering. Where must a finger be placed to produce a note of C (528 Hz)?

21.

The lowest frequency of a stretched string is 30 s^-1 when the supports are 60 cm apart. What is the speed of propagation of a wave in the string?

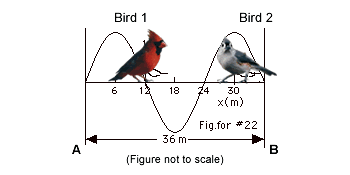
22.

Two birds sit on a telephone wire, as shown in the figure below. The wire is rigidly attached to the poles at A and B.  A person at pole A wishes to dislodge bird 2 without disturbing bird 1. She sets up a standing wave with a velocity of 48 m/s. (a) What is the longest wavelength that will get the job done? (b) At what frequency should she shake the wire in order to make such a wave? (c) If bird 2 can hold on only if his up-and-down acceleration is less than 48 m/s², what is the smallest amplitude needed to dislodge bird 2?

 

23.

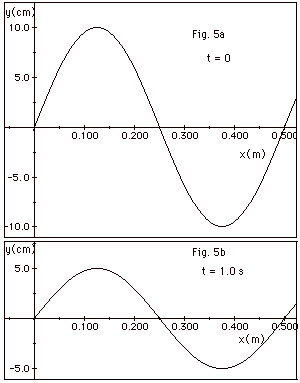
24.

A standing wave is set up in a long rope.  At t = 0 the standing wave with maximum displacement of its antinodes looks like Fig. 5a below. One second later (for the first time) it looks like Fig. 5b below. Find (a) the wavelength and (b) the period of the wave. (c) If the total length of the rope is 1.25 m, is the rope fixed at both ends, or is it fixed at one end and free at the other? (d) Write the equation of the standing wave. (e) What are the three longest wavelengths for standing waves in the string? Sketch the corresponding standing waves.

25.

What are the boundary conditions for a string (a) fixed at x = 0 and x = L and (b) fixed at x = 0 and free at x = L? Explain the reasons for these conditions. Use these conditions to find the allowed (c) wavelengths and (d) frequencies for a string (i) fixed at x = 0 and x = L and (ii) fixed at x = 0 and free at x = L.

26.

The stationary siren on a firehouse is sounding at 85 Hz. What is the frequency received by a firefighter racing toward the station with a speed of 108 km/hr (30 m/s)? Take the velocity of sound v = 340 m/s.

27.

A policeman is chasing a speeder along a straight interstate highway. Both the speeder and the policeman are moving at 144 km/hr. The siren on the police car has a frequency of 2.0 x 10³ Hz. What frequency is detected by (a) the policeman, (b) the speeder, and (c) and the observer standing by the side of the road as the cruiser approaches the observer? Take the velocity of sound v = 340 m/s.

28.

An ambulance travels down a highway at a speed of 30 m/s. Its siren emits sound at a frequency of 400 Hz. What is the frequency of the sound heard by a passenger in a car that is traveling at 20 m/s as (a) the car approaches the ambulance and (b) the car moves away from the ambulance? Take the velocity of sound v = 340 m/s.