Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 107

Answers - One Dimensional Motion

1.
  1. The distance moved x divided by the time t equals the constant velocity v. x/t = v  or  x = vt = 15 m/s (2.0 s) = 30 m.

  2. Since x/t = v = constant, the distance moved is directly proportional to the time elapsed. If you double the time, you double the distance.
    For t = 4.0 s, x = 2 x 30 m= 60 m.

2.
In general for constant acceleration, the distance moved by the object x =
xo + vot + 1/2 at2, where xo is the position of the object at t = 0 (the initial position), vo the velocity at t = 0 (the initial velocity), a the acceleration, and t the time at which you wish to find x.  Let's arbitrarily take xo = 0.  Then for an object initially at rest,  vo = 0,  x = 0 + 0 + 1/2 at2.
  1. x(2.0 s) = 1/2 (10 m/s2)(2.0 s)2 = 20 m

  2. x(4 s) = 1/2 (10 m/s2)(4 s)2 = 80 m. For constant acceleration and an initial position and initial velocity of zero, x = 1/2 at2  or  x/t2 = 1/2 a = a/2 = a constant. For this case x is directly proportional to the square of t. If you double t, t2 goes up by a factor of four and x must go up by a factor of 4 = 4 x 20 m = 80 m.

  3. For this part, we still take the initial position xo = 0, but now the initial velocity vo = 4.0 m/s.  x(t) = 0 + vot + 1/2 at2.
    x(2.0 s) = 0 + (4.0 m/s)(2.0 s) + 1/2 (10 m/s2)(2.0 s)2 = 28 m

  4. x(4.0 s) = 0 + (4.0 m/s)(4.0 s) + 1/2 (10 m/s2)(4.0 s)2 = 96 m

    With x = vot + 1/2 at2 and x/t2 = vo/t + a/2. Since t is a variable, the right hand side of the above equation is not equal to a constant and x is no longer proportional to the square of the time, that is, 96 ≠ 4 x 28.

3.
By the definition of constant acceleration, a = (v - vo)/(t - 0), where v is the velocity of the object at time t and vo is the velocity of the object at time t = 0.
  1. a = {(60 - 20) m/s}/(2.0 s - 0) = 20 m/s2

  2. Taking xo = 0, x(t) = vot + 1/2 at2.
    x(2.0 s) = 20 m/s(2.0 s) + 1/2 (20 m/s2)(2.0 s)2 = 80 m.

4.
  1. The average velocity = x/t = (v + vi)/2, where v = 15 m/s and vi is the initial speed. The average speed = x/t = 60 m/6.0 s = (15 m/s + vi)/2  or 10 m/s = (15 m/s + vi)/2  or  20 m/s = 15 m/s + vi so vi = 5 m/s.

  2. The acceleration a = (v - vi)/(t - ti) = (15 m/s - 5 m/s)/(6.0 s) = 5/3 m/s2.

  3. vi2 = vo2 + 2a(xi - xo).
    (5 m/s)2 = 0 + 2(5/3 m/s2)(xi - xo)
    25 m2/s2 = (10/3 m/s2)(xi - xo)
    or  (xi - xo) = 7.5 m.
Let's check all of this. First we find the time for the object to acquire a velocity vi = 5.0 m/s with an acceleration of 5/3 m/s2 starting from an initial velocity of zero.  v = vo + at  or  5.0 m/s = 0 + (5/3 m/s2)t  or  t = 3.0 s.

At t = (6.0 + 3.0)s, x(9.0 s) = 1/2 (5/3 m/s2)(9.0 s)2 = 67.5 m = 60 m + 7.5 m, where 60 m is the distance given in the statement of the problem for the object to go from 5 m/s to 15 m/s and 7.5 m is the distance moved from the point where the object was at rest to where it was traveling with 5 m/s.

5.
Three equations are used frequently for motion with constant acceleration: For motion in the y-direction,
  1. v(t) = vo + at
  2. y(t) = yo + vot + 1/2 at2,   and
  3. v2(y) = vo2 + 2a(y - yo)
The first is just the definition of constant acceleration, a = (v - vo)/(t - 0), rearranged algebraically. Eq. 1 gives the velocity of an object as a function of time. If you know the initial velocity vo and the acceleration a of the object, you can find its velocity v at time t. The second equation is derived from the area under the velocity versus time curve and the definition of acceleration (See solution to Problem #16). It gives the position y as a function of t. If you know the initial position yo of the object, vo and a, you can find y for any time t. The third equation is found by solving for t in Eq. (1) and substituting it into Eq. (2). It gives the velocity v as a function of height y. If you know yo, vo, and a, you can find y for any value of v.
  1. We know the height reached y, the time t for it to reach this height, the acceleration a of the ball, and taking yo = 0, we can find the one unknown vo with:
    40 m = 0 + vo(2.0 s) - 1/2 (10 m/s2)(4.0 s2)
    40 m = vo(2.0 s) - 20 m  or
    vo = 30 m/s

  2. v(2.0s) = vo + at = 30 m/s - 10 m/s2(2 s) = 10 m/s

  3. We must interpret the meaning of "how much higher will the ball go." The answer, of course, is "until it stops rising." At the highest point the ball comes momentarily to rest and v(t) = 0.

    0 = v2 = vo2 + 2a(y - yo) = (30 m/s)2 - 20 m/s2(y - 0)  or
    0 = 900 m2 - 20 m(y)  and  y = 45 m.
    Added height = (45 - 40)m = 5 m.

6.
  1. We do not know the time, but taking yo = 60 m and y = 0, we can use
    v2(y) = vo2 + 2ay(y - yo)
    v2(0) = (-20 m/s)2 - 20 m/s2(0 - 60 m) = (400 + 1200)m2/s2
    and v = -40 m/s, where the negative sign occurs because we have taken up as positive.

  2. v(t) = vo + at  or  -40 m/s = -20 m/s - 10 m/s2 t and t = 2 s

  3. Now the initial and final positions are the same, but the initial velocity vo = +20 m/s. The algebra, however, will be the same as in part (a) and the answer is again v = -40 m/s when it hits the ground. The time does change with v(t) = vo + at and vo = +20 m/s:
    -40 m/s = 20 m/s -10 m/s2 t and now t = 6 s.

7.
  1. i.  By definition, the slope of a plot of x as a function of t at any time t is
    dx/dt. Since v = dx/dt, the slope of a plot of x as a function of t at any time t is the velocity at that instant.

  2. ii.  If you plot y as a function of x, you know that ∫y dx is the area under the curve of y versus x. Similarly, ∫v dt is the area under the velocity v versus time t curve up to time t. Since ∫dx = ∫v dt, the area under the velocity v versus time t up to time t is the distance moved.

  3. ii.  By definition, the slope of v versus t at any instant is dv/dt.
    Since a = dv/dt, the slope of v versus t at any instant is the acceleration at that instant.

  4. iii.  ∫a dt is the area under the a versus t curve. Since ∫dv = ∫a dt, the area under the a versus t curve up to any time t is the change in velocity in that time interval.

8.

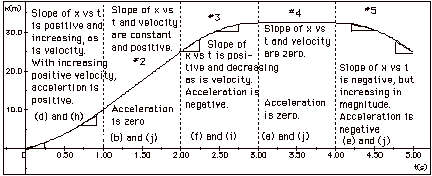
The answers are written on the graph below for each interval. Note that in #1 the slope of the x vs t curve is positive and increasing in magnitude so the velocity is positive and increasing and the acceleration is positive. In #3 the velocity is positive, but decreasing in magnitude so the acceleration is negative. In #5 the velocity is negative, but it is increasing in magnitude so the acceleration is negative.

9.
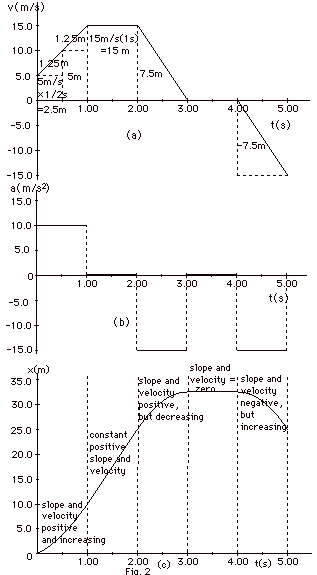
See Figure 2 below:
  1. The acceleration at any instant equals the slope of v versus t at that instant.

    From t = 0 to t = 1.0 s, a = (15 - 5)m/s/(1 - 0 )s = 10 m/s2.
    From t = 1.0 s to 2.0 s, the velocity is constant and the acceleration a = 0.
    From t = 2.0 s to 3.0 s, a = (0 - 15.0)m/s/(3.0 - 2.0)s = -15 m/s2.
    From t = 3.0 s to 4.0 s, the velocity equals zero and the acceleration a = 0. From t = 4.0 s to 5.0 s, a = (-15.0 - 0)m/s/(5.0 -4.0)s = -15 m/s2.

  2. The distance moved by an object in time t equals the area under the v vs t curve from t = 0 to t.

    From t = 0 to t = 0.5 s, area equals the area of a triangle of height
    5.0 m/s and base 0.5 s and square with sides= 5.0 m/s and 0.5 s.
    Area = (1/2)(5.0 m/s x 0.5 s) + (5 m/s x 0.5s) = 3.75 m.

    From t = 0.5 s to t = 1.0 s,
    area = (1/2 x 5.0 m/s x 0.5 s) + (10 m/s x 0.5 s)= 6.25 m.

    From t = 0 to t = 1, x(1s) = (3.75 + 6.25)m =10 m.

    From t = 1 to t = 2 s, area = 15 m/s x 1 s = 15 m.
    x(2s) = (10 + 15) m = 25 m.

    From t = 2 s to t = 3 s, area = 1/2(15 m/s)(1s) = 7.5 m.
    x(3s) = (25 + 7.5)m = 32.5 m.

    From t = 3 to 4 s, the area = 0.
    x(4s) = 32.5 m.

    From t = 4 to 5 s, area = 1/2(-15 m/s)(1 s) = -7.5 m.
    x(5s) = (32.5 - 7.5)m = 25 m.

  3. The slope of x vs t at any instant is the velocity at that instant.

    From t = 0 to t = 1 s, the slope and velocity are positive and increasing. From t = 1 to t = 2 s, the slope and velocity are constant and positive.
    From t = 2 to t = 3 s, the slope and velocity are positive, but decreasing. From t = 3 to t = 4 s, the slope and velocity equal zero.
    From t = 4 to t = 5 s, slope and velocity are negative, but increasing.

    All agree with v versus t in Fig. 2a.

10.
  1. "Coming to rest in a distance of 20 m" means x(t) - xo = 20 m.

    v2(x) = vo2 + 2a(x - xo)
    0 = (10 m/s)2 + 2a(20 m)
    (-40a) m = 100 m2/s2
     a = -2.5 m/s2.

  2. v(t) = vo + at
    0 = 10 m/s - (2.5 m/s2)t
    t = 4.0 s.

  3. Shown in the figure below

  4. Shown in the figure below

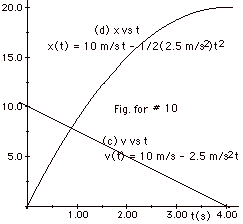
11.
The average velocity of the flowerpot equals:
2.0 m/0.10 s = 20 m/s  ≈ v
at top or bottom of window.

v2(y) = vo2 + 2a(y - yo) or (-20 m/s)2 = 0 + 2(-10 m/s2)(0 - yo) or yo = 20 m. Since the distance between floors is 4.0 m, it fell from an apartment 5 floors up or, since she is on the fifth floor, from an apartment on the tenth floor.

12.

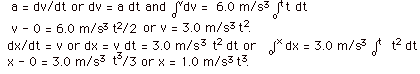
13.


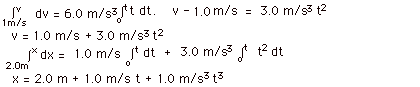
14.
The change in velocity up to any time equals the area under a versus t curve up to that time. The distance moved in time t equals the area under the v versus t curve up to that time t.
  1. Velocity as a function of time and position as a function of time are shown in the figure below.



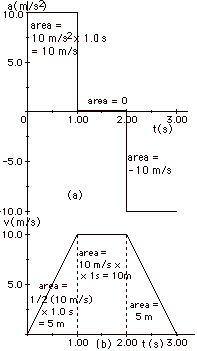
  2. Velocity as a function of time and position as a function of time are shown in the figure above.

  3. The maximum velocity occurs for t = 1.0 s through 2.0 s and it is equal to
    10 m/s, as illustrated in figure 3b above.



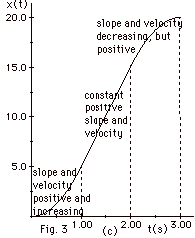
  4. The distance moved by the particle in 3.0 s is 20.0 m. Notice that the slope of x vs t at any instant equals the velocity v at that instant and the slope of v vs t at any instant equals the acceleration a at that instant.

15.
  1. For the ball thrown downward, y(t) = yo + vot + 1/2 at2  or
    taking up as +,
    y(t) = 40 m - (8.0 m/s)t - (5.0 m/s2)t2      (Equation 1)
    For the ball thrown upward from the ground,
    y(t) = 0 + (12 m/s)t - (5.0 m/s2)t2           (Equation 2)
    When the balls collide the two y's are equal:
    40 m - (8.0 m/s)t - (5.0 m/s2)t2 =
                              0 + (12 m/s)t - (5.0 m/s2)t2  or
    40 m - (8.0 m/s)t = (12 m/s)t
    40 m = (20 m/s)t  and  t = 2.0 s.

  2. From Eq. 2, y(2.0s) = (12 m/s)(2.0 s) - (5.0 m/s2)(2.0s)2 = 4.0 m
    From Eq. 1, y(t) = 40 m - (8.0 m/s)(2.0 s) - (5.0 m/s2)(2.0 s)2= 4.0 m.

  3. In general, v(t) = vo+ at.
    For the second ball, v(2.0 s) = 12 m/s - (10 m/s2)(2.0 s) = -8.0 m/s.
    Since the velocity at 2.0 s of the second ball is negative, it is on its way down when the first ball collided with it.

16.
In Fig. 4 below, I have used v’ and t’ as a variable velocity and time, respectively, to distinguish between the velocity v at time t.

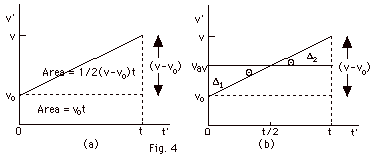
  1. The distance moved by the object in time t equals the area under the velocity as a function of time curve up to time t. In Fig. 4a, the area consists of the area of a triangle of base t and height (v - vo) and a rectangle of length t and height vo.

    In time t, the distance traveled x = 1/2 (v - vo)t + vot = (vo + v)/2t.
    The average velocity vav= x/t = (v + vo)/2.

    If the object were to move in a straight line with the average velocity for the same time t as the object that moved with a variable velocity, it would have the same displacement. In Fig. 4b, we see that the triangles labeled Δ1 and Δ2 are congruent because their angles are equal and the heights, (vav – vo) and (v – vav), are equal. Thus the rectangle with height vav and length t has area vavt which equals 1/2 (v - vo)t + vot,  the area used in Fig. 4a.

  2. Since Δ1 and Δ2 are congruent, their bases are equal. For this to be true, the time at which the velocity equals the average velocity occurs at t/2 or halfway through the interval.

    In Problem #5, I mentioned that you could find x(t) from Fig. 4.
    Since a = (v - vo)/t   or  (v - vo) = at, we write:
    1/2 (v - vo)t + vot = 1/2 at2 + vot = vot + 1/2 at2
    = distance traveled
    If there is an initial displacement of xo,  x(t) = xo + vot + 1/2 at2.

17.
  1. In Fig. 17a below, at t = 1 s, the velocity is zero
    (the slope of x vs t at t = 1 s is zero).

    The acceleration is positive because the slope of x versus t after t = 1 s is positive and increasing. For example, imagine the slope of x vs t at t = 2 s is 1 cm/s, then a = [(1 - 0)cm/s]/(2 - 1) s = +1/2 cm/s2.



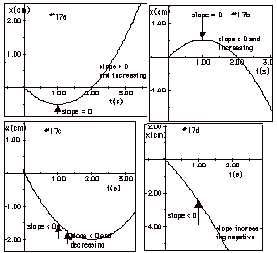
  2. In Fig. 17b above, at t = 1 s, the velocity is zero
    (the slope of x vs t at t = 1 s is zero).

    The acceleration is negative because the slope after t = 1s is less than zero and increasing. For example imagine the slope of x vs t at t = 2 s
    is -1 m/s, then a = [(-1 - 0)cm/s]/(2 - 1)s = -1/2 cm/s2.

  3. In Fig. 17c, at t = 1 s, the velocity is negative
    (the slope of x vs t at t = 1 s is negative).

    The acceleration is positive because the slope of x vs t after t = 1 s is negative and decreasing. For example imagine the slope of x vs t at
    t = 1 s is -1 cm/s and at t = 2 s it is 0. Then a = {0 - (-1)cm/s}/(2 - 1)s
    = 1/2 cm/s2.

  4. In Fig. #17d, at t = 1 s, the velocity is negative
    (the slope of x vs t at t = 1 s is negative).

    The acceleration is negative because the slope of x vs t is negative and increasing. For example, imagine at t = 1 s, v = -3 m/s and at t = 2 s,
    v = -4 m/s, then a = {(-4) - (-3)}cm/s/(2 - 1)s = -1/2 cm/s2.

  5. The speed, the magnitude of the velocity, is increasing at t = 1 s for all cases except (c).

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
October 8, 2002
April 15, 2003