|
|
|
1.
|
a. For constant linear velocity, the ratio of
the distance x moved to the time t,
x/t = constant = v or
x = vt.
b. For constant angular velocity, the ratio of the
angle Θ moved to the time
t,
Θ/t = constant
= ω or
Θ= ωt.
|
|
|
2.
|
a. Constant linear acceleration a equals the change
in linear velocity
divided by the time to change
the velocity, or
a = (v - vo)/(t - 0) or
v = vo + at.
b. Constant angular acceleration α
equals the change in angular velocity
divided by the time to change the velocity,
or
α = (ω
- ωo)/(t -
0) or
ω = ωo
+ αt.
|
|
|
3.
|
| a. |
dx/dt
= v = vo + at or |
b. |
dΘ/dt
= ω = ωo + αt
or |
| |
 |
|
 |
|
|
|
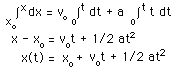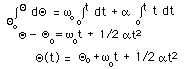4.
|
- ω(t) = ωo
+ αt.
ω(4.0 s) = πs-1
+ (4 π s-2)(4.0
s) =17 πs-1.
- Θ(t) = Θo
+ ωot + 1/2
αt2.
Θ(4.0s) = 0 + ( π
s-1)(4.0s) + 1/2 (4 πs-2)(16s2)
= 36 π.
In one rotation, the wheel turns through an angle of 2 π
radians.
The number of turns made by the wheel = 36 π/2 π
= 18.
|
|
|
5.
|
- ω(t) = dΘ/dt
= d(b + ct + et2)/dt = c + 2et.
ω(t1) = c
+ 2et1
- α(t) = dω/dt
= d(c + 2et)/dt= 2e = constant = α(t1).
- v(t1) = ω(t1)r
= (c + 2et1)r.
- Tangential acceleration, a(t1) = α(t1)r
= 2er.
- Centripetal or radial acceleration(t1) = {
v(t1)}2/r = (c + 2et1)2r2/r
= (c + 2et1)2r.
|
|
|
6.
|
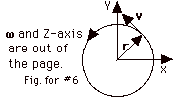
- If v = ω x
r, then v is perpendicular to ω and
v is perpendicular to r, or v is perpendicular
to the plane that contains ω
and r. In the figure above you see that
ω is out
of the page and v is in the xy-plane, so v
is perpendicular to ω.
Since v is always tangent to the path, it is
also perpendicular to r. The plane of ω and
r is the xz-plane, so v is perpendicular to
the plane that contains ω
and r. If you point the fingers of your
right hand in the direction of ω
(out of the page) and curl them in the direction of
r, your outstretched thumb points in the direction
of v. Also, v = ωr
sin
 ω,r
= ωr sin 90o =
ωr. ω x
r gives both the correct direction and magnitude
of v.
- a = ω
x (ω x
r) = ω x
v from above. a is into the center of
the circle and perpendicular to both ω
and v. If you point the fingers of your
right hand in the direction of ω
(out of the page) and curl them in the direction of
v, your outstretched thumb points in the direction
of a or into the center of the circle. a =
ωv sin w,
v = ωv
sin 90o = ωv
= (v/r)(v) = v2/r = ω2r.
The direction and magnitude of the centripetal acceleration
is given by:
a = ω
x (ω x
r) = ω x
v.
|
|
|
7.
|
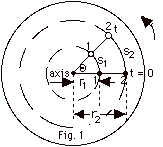
The constant angular velocity ω
= (Θ - 0)/(t - 0) = Θ/t.
In time t, both points 1 and 2 rotate through angle
Θ so both points have the
same angular velocity. For point 1, v1 = s1/t
and for point 2, v2 = s2/t.
Since s2 > s1, v2 >
v1. This is also shown from v1 =
ωr1 and v2
= ωr2.
Again since r2 > r1, v2
> v1.
|
|
|
8.
|
For one particle of mass m and velocity
v, the kinetic energy
K = 1/2 mv2.
For all of the particles that make up the disk from i = 1 to
i = N,
K = 1/2 m1v12 +
1/2 m2v22 + 1/2 m3v32
+ . . . .1/2 mNvN2.
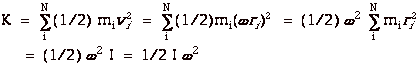
where I is the moment of inertia of the rigid body.
|
|
|
9.
|
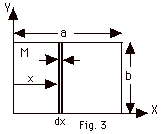
The area of the plate A = ab (Fig. 3 above).
The mass per unit area σ
= M/A = M/ab.
The differential area with height b and thickness dx is dA =
b dx.
The mass of this area is the mass per unit area times dA.
That is dm = σ dA = (M/ab)
(b dx) = M dx/a.
Its moment of inertia dI = x2 dm = x2
(M dx/a) = (M/a) x2 dx.
The moment of inertia for the entire plate about the Y-axis
is:
|
|
|
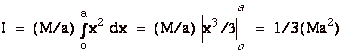
10.
|
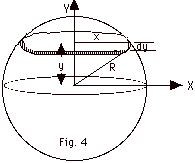
The differential volume of the disk of radius x and thickness
dy is dV = πx2
dy. Its mass dm = the mass per unit volume times the volume
=
dm
= ρ dV = {M/(4 πR3/3)}
{ πx2 dy). dI
=1/2 dm x2 =
1/2{M/(4 πR3/3)}{
πx2
dy)x2.
From Fig. 4, we see that x2 = (R2
- y2) and
dI = 3M/8R3 (R2 - y2)2
dy.
|
|
|
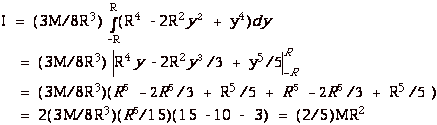
11.
|
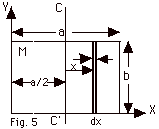
- I = iσ
miri2. The
moment of inertia of the plate about the Y-axis is greater
than the moment of inertia about CC’ because the mass
of the plate is less concentrated about the Y-axis than
CC’. In other words, there are greater values
of r for the Y-axis calculation.
- Again dI = (M/a) x2 dx. But taking
x = 0 at C’, we must integrate from -a/2 to a/2:
- CC’ passes through the center of mass of the plate.
The parallel axis theorem states that the moment of inertia
about a parallel axis a distance d from an axis through
the center of mass equals the moment of inertia about the
center of mass + Md2. In this case
IY = ICC’ + M(a/2)2
since the distance between the Y-axis and CC’ is
a/2.
1/3 Ma2 = ICC’
+ Ma2/4 or
λCC’
= Ma2(1/3 - 1/4) = 1/12 Ma2.
|
|
|
12.
|
|
|
|
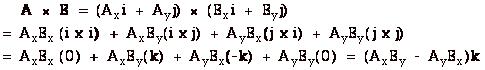
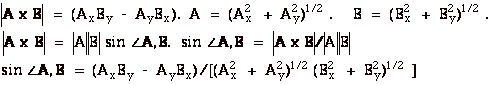
13.
|
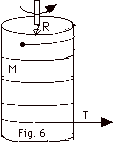
- The string is always tangent to the surface of the cylinder.
The angle between the tension and the radial vector is 90o.
The torque applied to the cylinder is constant and
has magnitude
τ = RT
sin 90o = 0.040 m(3.0 N))(1) = 0.12 N-m.
The moment of inertia of the cylinder about its axis is
I = 1/2 MR2 = 1/2(30 kg)(0.040 m)2
= 2.4 x 10-2 kg-m2.
α = τ/I
= 0.12 N-m/2.4 x 10-2 kg-m2 = 5.0
s-2.
- The angular speed at t = 2.0 s is
ω = ωo
+ αt = 0 +(5.0 s-2)(2.0 s) = 10
s-1.
|
|
|
14.
|
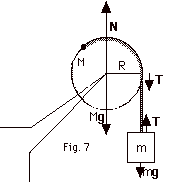
- Applying Newton's second law to the hanging block,
Fnet = ma
mg - T = ma
(Equation
1)
For the accelerated disk and taking clockwise rotation as
positive,
τnet
= Iα
RT sin 90o = 1/2 MR2 α =
1/2 MR2 (a/R)
T = 1/2 Ma
(Equation
2)
Substituting Eq. 2 into Eq. 1:
mg - 1/2Ma = ma
a = mg/(M/2 + m)=(0.50 kg)(10 m/s2)/(1.0/2
+ 0.5)kg = 5.0 m/s2.
- Applying Newton's second law to the disk,
(Fnet)y = may
N - Mg - T = m(0) = 0 or
N = Mg + T (Equation
3)
From Eq. 2,
T = 1/2 Ma = 1/2 (1.0 kg)(5.0 m/s2)
= 2.5 N
N = Mg + T = (1.0 kg)(10 m/s2) + 2.5 N = 12.5
N
|
|
|
|
|
16.
|
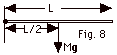
- As illustrated in Fig. 8 above,
τabout
pivot = Iabout pivot α
L/2(Mg)sin 90o = 1/3 ML2
α
α
= 3/2 (g/L)
- a = αL = 3/2(g/L)
(L) = 3g/2
|
|
|
17.
|
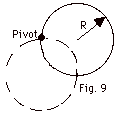
The moment of inertia of the disk about the pivot in Fig. 9
above is
I = ICM + Md2,
where d the distance of the center of mass from the pivot is
R. Thus,
Ipivot = 1/2 MR2 + MR2
= 3MR2/2.
For the hoop in part (c)
Ipivot = MR2 + MR2 =
2MR2.
Take the "final" gravitational potential energy Uf
= 0. Then the initial gravitational potential energy,
when it is in the position shown by the solid circle,
Ui = MgR, since the center of mass of the disk
in its initial position is a distance R above its "final"
position. Because it is initially at rest, Ki
= 0.
From conservation of energy,
Ui
+ Ki
= Uf
+ Kf
MgR +
0
= 0
+ 1/2(3/2MR2)ω2
- ω = 2(g/3R)1/2
and at the center of mass v = ωR
= 2(gR/3)1/2
- At the bottom of the disk, v = ω2R
= 4(gR/3)1/2
- Now,
MgR +
0
=
0
+ 1/2(2MR2)ω2 and
ω = (g/R)1/2
At center of mass v = R(g/R)1/2 = (gR)1/2.
At bottom v = 2(gR)1/2.
|
|
|
18.
|
The center of mass of the disk translates
and the disk rotates. The total kinetic energy of the disk is
the sum of its translational and rotational kinetic energy =
1/2 Mv2 + 1/2 Iω2
= 1/2 Mv2 + 1/2(1/2 MR2)(v/R)2
= 3/4 Mv2.
|
|
|
19.
|
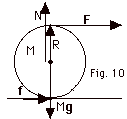
The forces acting on the spool are F, its weight W, normal
force N, and the frictional force f. f acts to
the right because when you pull it to the right, the spool
would tend to slip backwards. A frictional force then acts
on it to the right. Taking the axis of rotation about the
center of the sphere means that the weight and normal force
produce no torque since their lines of action passes through
the center of the sphere. The force F produces clockwise rotation,
while f produces counterclockwise rotation.
τ
= r x F
For translation,
Fnet = Ma
F + f = Ma
(Equation 1)
For rotation,
τnet =
Iα
RF -Rf = 1/2 MR2 (a/R) or
F - f = 1/2 Ma (Equation
2)
Adding Eq. 1 and Eq. 2:
2F = 3/2 Ma or
a = 4F/3M
From Eq. 1,
F + f = Ma, with Ma = 4F/3, F
+ f = (4F/3) or
f = F/3.
|
|
|
20.
|
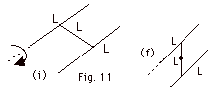
Use conservation of energy. This time take the potential energy
of the initial state (Fig. 11i) as the zero of potential. The
final potential energy state (Fig. 11f) will be negative. The
leg of the H about which the system rotates remains at rest.
Its potential energy is zero at all times. The center leg of
the H center of mass moves down to L/2 and the other leg moves
down L. The kinetic energy is gained by the center leg with
moment of inertia 1/3 ML2 about one end and the leg
on the right whose mass acts at the center of mass and has the
moment of inertia of a point particle ML2.
Ui + Ki =
Uf
+
Kf
0 + 0 = - (MgL/2 + MgL) + 1/2(1/3
ML2)ω2
+ 1/2(ML2)ω2
MgL(1/2 + 1) = (1/2 ML2ω2)(1/3
+ 1)
3/2(g/L)1/2 = ω
|
|
|
21.
|
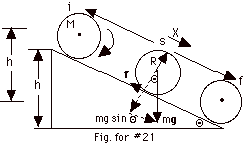
- The frictional force f acts at a point, not through
a distance, so it does no work and energy is conserved.
We take the gravitational potential energy of the sphere
equal to 0 at the bottom of the hill, that is, Uf
= 0. The center of mass of the sphere at the top of the
hill is a distance h above where it is at the bottom
of the hill: Ui = Mgh. As the sphere rolls down
the hill, it has kinetic energy of translation of the center
of mass and it has rotational kinetic energy. From conservation
of energy,
Ui + Ki = Uf + Kf
Mgh + 0 = 0 + 1/2 Mv2 + 1/2 Iω2
= 0 + 1/2 Mv2 + 1/2(2/5MR2)(v/R)2
Mgh = 7/10 Mv2 or
v = (10gh/7)1/2
- (Fnet)x
= ma
Mg sin Θ - f =
Ma (Equation
1)
Take the torques about the center of mass. Since the weight
and normal force pass through this axis, they produces no
torque.
τ
= Ia
Rf sin 90o = (2/5 MR2)(a/R)
f
= 2/5 Ma (Equation
2)
- Substituting Eq. 2 into Eq. 1:
Mg sin Θ
- 2/5 Ma = Ma or
a = 5g sin Θ/7
- From Eq. 2,
f = 2/5 Ma = (2/5)M(5g sin Θ/7)
= 2 Mg sin Θ/7
- v2 = vo2 + 2as =
0 + 2(5g sin Θ/7)s
=
(10g/7)(s sin Θ)
=
(10g/7)(h)
v = (10gh/7)1/2,
as found in Part (a).
|
|
|
22.
|
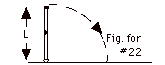
Assume the center of mass of the pencil is at its center L/2
(as shown in Fig for #22 above). From conservation of
energy,
Ui +
Ki = Uf + Kf
mgL/2 + 0 = 0 + 1/2 Iω2
ω = (mgL/I)1/2
= (mgh/1/3 mL2)1/2 = (3g/L)1/2
vtop of pencil = ωL
= (3g/L)1/2L = (3gL)1/2
|
|
|
23.
|
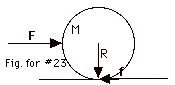
From Newton's second law:
Fnet = ma
F - f = Ma (Equation
1)
For rotation about center,
τnet
= Ia
Rf sin Θ = (1/2 MR2)(a/r)
f
= 1/2 Ma (Equation
2)
- Adding Eq. 2 to Eq.1:
F = 3/2 Ma or
a = 2F/3M (Equation
3)
- Substituting Eq. 3 into Eq. 2:
f = 1/2 M (2F/3M) = F/3
|
|
|
|
|
25.
|
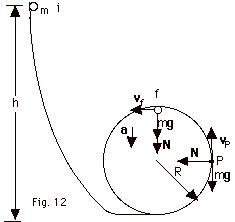
- Use conservation of energy to solve the problem. Take
the gravitational potential energy equal to 0 at the bottom
of the loop-the-loop. Remember that the sphere will have
both rotational and translational kinetic energy. The sphere
is released at the initial position i so the kinetic energy
there is zero. The sphere will make it around the loop-the-loop
if it can stay on the loop as it moves down from the top
of the loop. For this reason we take the top of the loop
as the final position f.
Ui + Ki = Uf + Kf
mgh + 0 = 2mgR + 1/2 mv2 + 1/2 Iω2
or
mgh = 2mgR + 1/2 mvf2 + 1/2 (2/5mR2)(vf/R)2
mgh= 2mgR + 7/10 mvf2
(Equation
1)
At the top, the acceleration is in toward the center.
Fnet = ma
mg + N = mvf2/R.
For the minimum height h, we want the minimum velocity vf,
so we set the normal force N = 0. Then,
mg = mvf2/R or
mvf2 = mgR
(Equation
2)
Substituting Eq. 2 into Eq. 1:
mgh = 27/10 mgR or
h = 2.7R.
- At P, the potential energy = mgR.
Now,
Ui + Ki = UP
+ KP
mg(2.7R) + 0 = mgR + 0.7mvP2
mg(2.7 - 1.0)R = 1.7mgR = 0.7mvP2
or
mvP2 = 17/7 mgR.
At P, the normal force produces the centripetal acceleration
into the center of the circle. At P, mg is
down.
Fnet = ma
N = mvP2/R = {(17/7)mgR}/R = 17/7
mg
|
|
|
26.
|
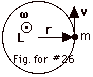
- L = r x mv. L is out of the
page (Fig. for #26 above).
L = rmv sin r,
v= rmv sin 90o = rmv.
- Since v = ωr, L
= (mr2)ω = Iω.
|
|
|
27.
|
|
|
|
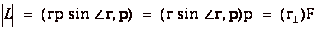
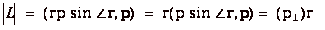
28.
|
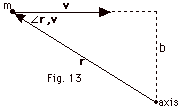
L = r x mv. L is into the page
(Fig. 13 above).
L = rmv sin r,
v = mv(r sin r, v) =
mvb.
|
|
|
29.
|
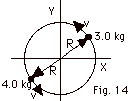
L = r x mv.
L is out of the page for both particles (Fig. 14 above).
L = rmv sin r,
v = rmv sin 90o.
Total L = 0.50 m(5.0 m/s)(3.0 + 4.0) kg = 17.5 kg-m2/s.
|
|
|
30.
|
L
= r x mv
dL/dt = d(r x mv)/dt = r x d(mv)/dt
+ dr/dt x mv
=
r x F + (v x mv)
= r
x F + (0)
= r
x F.
Note: d(mv)/dt = dp/dt = F and (v
x v) = 0.
|
|
|
31.
|
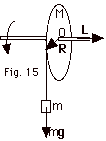
- τ = R x
mg is toward the right (Fig. 15 above)
τ= Rmg sin 90o
= Rmg
- L = 1/2 MR2 ω
+ Rmv = 1/2 MR2(v/R) + Rmv = vR(M/2 + m)
dL/dt = d[vR(M/2 + m)]/dt = R(M/2 + m) dv/dt
dL/dt = R(M/2 + m)a = Rmg = τ.
a = mg/(M/2 + m)
|
|
|
32.
|
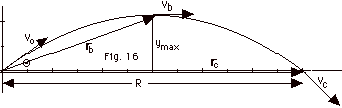
- At the origin, r = 0 and L = r x mv
= 0.
- At highest point, vy2 = 0
= (vo sin Θ)2
-2g(ymax - yo).
Since yo = 0, ymax = (vo
sin Θ)2/2g.
rb = rbx i + (vo
sin Θ)2/2g
j.
vb = vo cos Θ
= vox because vby = 0 and there
is no acceleration in the X-direction.
vb =vo cos Θi.
Lb = rb x mvb
= (rbx i + (vo sin Θ)2/2g
j) x m(vo cos Θi)
= (rbxmvo
cos Θ)(i x
i) + (mvo3 sin2
Θ cos
Θ/2g) (j
x i)
= (rbxmvo
cos Θ)(0) + (mvo3
sin2 Θ
cos Θ/2g)(-k)
= - (mvo3
sin2 Θ
cos Θ/2g)k
- The length of rc is the range R = 2vo2
sin Θcos Θ/g.
rc = 2vo2 sin Θcos
Θ/g i.
vc = vo(cos Θi
- sin Θ j).
When the projectile leaves the ground and returns to the
ground, the X-component of the velocity remains the same
(constant horizontal velocity) and the Y-component has the
same magnitude as the initial Y- component of velocity,
but now it is negative.
Lc = rc x mvc
= (2vo2
sin Θcos Θ/g)
i x mvo (cos Θi
- sin Θj)
= - (2mvo3
sin2 Θcos
Θ/g)k.
- ΔL is in -k
direction.
τ = r
x -mgj = (rxi + ryj)
x -mgj = -rxmg k.
|
|
|
|
|
34.
|
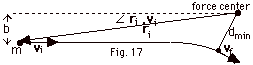
Take the axis at the force center (Fig. 17 above). The repulsive
force acts along the line connecting the two masses,
passing through the axis, so the net torque equals zero and
angular momentum is conserved.
Li = rimvi sin ri,
vi = (ri sin ri,
vi)mvi = bmvi.
Lf = dminmvf.
From conservation of momentum,
bmvi = dminmvf
and vf = bvi/dmin (Equation
1)
From conservation of energy,
Ui
+ Ki = Uf + Kf
0 + 1/2 mvi2 = A/dmin
+ 1/2 mvf2 (Equation
2)
Substituting Eq. 1 into Eq. 2:
1/2 mvi2 = A/dmin +
1/2 m(bvi/dmin)2
dmin2 - (2A/mvo2)dmin
- b2 = 0
dmin = {(2A/mvo2) ±
[(2A/mvo2)2 + 4b2]1/2}/2
dmin = (A/mvo2) + [(A/mvo2)2
+ b2]1/2
|
|
|
35.
|
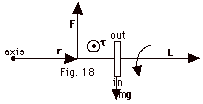
Curl the fingers of your right hand clockwise to find the
angular momentum L to the right (Fig. 18 above). τ =
r x F is out of the page. The torque due to
the weight of the wheel is into the page, but we have made
the torque due to F greater and the resultant torque is out
of the page. Since τ =
ΔL/ Δt,
ΔL will be in the
direction of τ,
out of the page or to the right as you view it from above.
The wheel turns to the right.
|
|
|
36.
|
d(L2)/dt = d(L . L)/dt
= L. dL/dt + dL/dt.
L = 2L . dL/dt = 2L
. τ
= 2Lτ cos L,
τ. If
the angle between L and τ
is 90o, d(L2)/dt = 0 and the magnitude
of the angular momentum remains constant.
|
|
|
37.
|
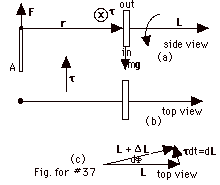
Taking the axis at A, F produces no torque because it
passes through the axis. τ
= r x mg. The torque due to mg is into
the page, as shown in Fig. for #37(a), a side view, and to
the left in Fig. for #37(b), a top view. The magnitude of
the torque τ =
rmg. Since τ
= dL/dt or dL = τ
dt, dL is to the left as shown in Fig. for #37(c),
a top view. The angle turned through by L is dΦ =
τ dt/L or dΦ/dt
= mgr/L = mgr/Iω. The
wheel precesses counterclockwise with dΦ/dt
so the platform must rotate with dΦ/dt
= mgr/Iω counterclockwise
for the wheel to maintain a fixed position relative to the
platform.
|
|
|
38.
|
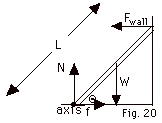
For equilibrium, Στ =
0.
Taking the axis at the bottom of the ladder, with τ
= r F sin r,
F,
Στ = L Fwall
sin Θ - (L/2)W
cos Θ = 0 or
tan Θ= W/2 Fwall
(Equation
1)
Note that neither N nor f contribute to the torque when the
axis is at the bottom of the ladder because both forces pass
through the axis. Also for equilibrium,
| σ Fx
= 0 and |
σ Fy
= 0 |
| f - Fwall =
0 |
N - W = 0 |
| f = Fwall |
N = W but f = µN
so f = µW and µW = Fwall (Equation
2) |
Substituting Eq. (2) into Eq. (1):
tan Θ= W/2µW
= 1/2µ = 1/0.80 = 1.25. Θ=
51.3o.
|
|
|
39.
|
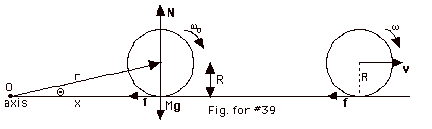
Take the axis at O in the above figure.
The torque due to Mg = rMg sin Θ
= Mg (r sin Θ) = MgR clockwise.
The torque due to the normal force N = rN sin Θ= NR counterclockwise.
Since there is no acceleration in the vertical direction,
N - Mg = 0 or N = Mg.
The torque due to Mg equals the torque due to N so that the
net torque due to these two forces is zero.
The torque due to the frictional force = fx sin
f, x-axis = fx sin 0o = 0.
Since no net torque acts on the sphere, angular momentum is
conserved. The initial angular momentum LI = Iωo
= 2/5 MR2ωo.
The final angular momentum when it is both rotating and the
center of mass moves with velocity v = Lf = Iω
+ MRv. For the sphere to rotate without slipping, v = ωR
or Lf = 2/5 MR2ω
+ MR2ω. From
conservation of angular momentum,
LI
= Lf
2/5 MR2ωo
= 2/5 MR2ω
+ MR2ω = 7/5
MR2ω
2ωo/ 7
= ω
|
|
|
|
