|
Answers - Center of Mass, Momentum,
and Collisions
|
|
|
1.
|
Impulse J = pf - pi = mvf
- mvi. Taking the return direction as positive,
J = 0.060 kg{(40 - (-50)}m/s = 5.4 kg-m/s.
|
|
|
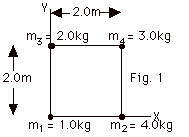
2.
|
XCM = (m1x1 + m2x2
+ m3x3 + m4x4)/(
m1 + m2 + m3 + m4)
=
{(1.0 kg)(0) + (4.0 kg)(2.0 m) + (2.0 kg)(0) + (3.0 kg)(2.0
m)}/(10.0 kg) = 1.4 m.
YCM = (m1y1 + m2y2
+ m3y3 + m4y4)/(
m1 + m2 + m3 + m4)
=
{(1.0 kg)(0) + (4.0 kg)(0) + (2.0 kg)(2.0 m) + (3.0 kg)(2.0
m)}/(10.0 kg) 1.0 m.
|
|
|
3.
|
- Taking east in the +i direction and north in the
+j direction,
J = pf - pi =
(1500 kg)(8.0 m/s)(j - i) = 12 x 103
kg-m/s(j - i).
- J = Fav t
Fav = J/t = {12 x 103
kg-m/s(j - i)}/3.0 s = 4 x 103
N(j - i).
- By Newton's third law of motion, the average force of
the car on the road = -4 x 103 N(j - i).
|
|
|
4.
|
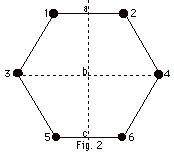
Divide the system into three pairs of particles, consisting
of 1 + 2, 3 + 4, and 5 + 6. The midway for 1 + 2 is at a and
the midpoint for 5 + 6 is c. We can treat 1 + 2 as a point particle
of mass of 2m at a and 5 + 6 as a point particle of mass 2m
at c. We can combine these two point particles to be another
point particle with mass 4m at b. 3 + 4 have their midpoint
at b so we can replace them with a point particle of mass 2m
at b. Finally the whole works acts like a point particle of
mass 6m at b.
|
|
|
5.
|
- pA = (1.0 kg)(4.0 m/s) = 4.0 kg-m/s.
pB = (2.0 kg)(2.0 m/s) = 4.0 kg-m/s.
- KA = 1/2(1.0 kg)(4.0 m/s)2 = 8.0
J.
KB = 1/2(2.0 kg)(2.0 m/s)2 = 4.0 J.
While the momenta are equal, the kinetic energies are not.
|
|
|
6.
|
Take the distance to the edge of the
rink as x. Then the velocity v1 after the collision
for the skater of mass m1 equals +x/12 s and the
velocity v2 of the other skater equals -x/18 s. From
conservation of momentum,
pi = pf
0 = (50 kg)(x/12 s) + (m2)(-x/18 s) or
(m2)(x/18 s) = (50 kg)(x/12 s)
m2 = (50 kg)((18/12) = 75 kg
|
|
|
7.
|
Take to the right to be positive. From
conservation of momentum,
pi
= pf
0.050 kg(0.20 m/s) + (0.10 kg)((-0.04 m/s) = (0.05 + 0.10)kg
vf
(0.010
- 0.004)kg-m/s = (0.15 kg)vf
vf
= 0.040 m/s to the right
|
|
|
8.
|
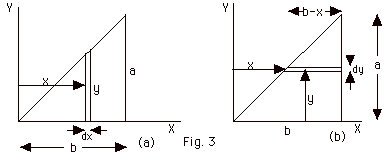
For Fig. 3a:
(a) The area of the triangle is 1/2 (base)(altitude) = ba/2.
(b) The mass per unit area σ
= mass/area = M/(ba/2) = 2M/ba.
(c) The area of the element dA = (y)dx.
(d) Since σ = mass/area,
the mass of any element equals σ
times the area of the element. dm = (σ)dA
= (2M/ba)ydx.
(e) dm x = (2M/ba)ydx (x)
(f) In general, the equation of a line is y = mx + b, where
m is the slope of the line and b is the intercept on the y-axis.
In Fig. 3, we see b = 0 and m = a/b, so y = (a/b)x.
(g) From the equation of the line found in (f) we substitute
y into dm x =
(2M/ba) y dx x, or dm x = (2M/ba) (a/b)x dx x = 2M/b2
x2 dx, and
(h)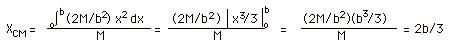
For Fig. 3b:
(a) and (b) The solutions to both (a) and (b) are the same
for both Fig. 3a and Fig. 3b.
(c ) dA = (b - x)dy
(d) dm = (2M/ba) (b - x)dy
(e) and (f) The solutions to both (e) and (f) are the same
for both Fig. 3a and Fig. 3b.
(g) from the equation of the line y = (a/b) x, x =
by/a
(h) y dm = y (2M/ba)(b - by/a)dy = (2M/ba) (b/a)(a - y)
y dy =
(2M/a2)(a - y) y dy
YCM = ∫ dm y/M = ∫(2M/a2)
(ay - y2) dy /M = 2/a2 |(ay2/2
- y3/3)|
taking the integral from 0 to a,
YCM = (2/a2) (a3/2 - a3/3)
= (2/a2) (3a3/6 - 2a3/6)
= a/3
|
|
|
9.
|
The center of mass of the four particles at the base of the
pyramid is the center of the base. The center of mass of the
five-particle system lies on the line perpendicular to the
base and passes through the peak of the pyramid. This line
passes through the center of mass of the four particles at
the base and gives the x-coordinate of the center of mass
at the center of the base.
YCM = {(m)(h) + (4m)(0)}/5m = h/5.
|
|
|
10.
|
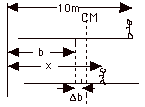
In the figure above, b represents the center of mass of the
barge and Δb the distance
the barge moves to the right as the man moves to the left. No
external forces act on the barge-man system and the center of
mass CM of this system remains at rest.
Initially, XCM = {(75 kg)(10 m) + (225 kg)(b)}/(75
+ 225)kg (Equation
1)
Finally, XCM = {(75 kg)x + (225 kg)(b + Δb)}/(75
+ 225)kg (Equation
2)
Since the CM of the system remains at rest, equate Eq. 1 and
Eq. 2 and cancel denominators,
(75 kg)(10 m) + (225 kg)(b) = (75 kg)x + (225 kg)(b + Δb)
(Equation 3)
Distance moved by man relative to shore = (10 m - x) = 2.0 m
- Δb
or Δb
= x - 8.0 m.
Substituting this expression for Δb
into Eq. 3:
750 N + (225 kg)(b) = (75 kg)x + (225 kg)(b + x - 8.0 m)
750 N + 1800 N = (300 kg)x and
x = 8.5 m.
|
|
|
11.
|
Momentum is conserved:
pi = pf
pin = p1f + p2f
Since the final momentum of product 1, p1f, =
- p2f, the negative of the final
momentumof product 2, the initial momentum pin
of the nucleus must equal zero.
|
|
|
12.
|
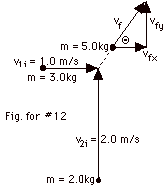
(pi)x
= (pf)x
(3.0 kg)(1.0 m/s) = (5.0 kg)(vf)x (vf)x
= 0.60 m/s
(pi)y
= (pf)y
(2.0 kg)(2.0 m/s) = (5.0 kg)(vf)y (vf)y
= 0.80 m/s
vf = {(0.60)2 + (0.80)2}1/2
= 1.0 m/s. tan Θ
= 0.80/0.60. Θ = 53o.
|
|
|
13.
|

| pi = pf |
mvo |
= |
mvo |
| Ki = Kf |
1/2 mvo2 |
= |
1/2 mvo2 |

| pi = pf |
mvo |
= |
mvo/2 + mvo/2 |
| Ki ≠
Kf |
1/2 mvo2 |
≠ |
1/2 m(vo/2)2
+ 1/2 m(vo/2)2 |
Another conservation law is at work here. In an elastic collision,
kinetic energy is also conserved. For an elastic collision,
(b) cannot occur.
|
|
|
14.
|
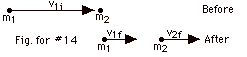
For an elastic collision,
pi
= pf
m1v1i = m1v1f
+ m2v2f
(Equation
1)
where I have assumed both final velocities to the right. In
any calculation, if one of them is to the left, you will get
a minus answer in your solution.
Ki
= Kf
1/2 m1v1i2 = 1/2 m1v1f2
+ 1/2 m2v2f2
(Equation
2)
Solving Eq. 1 and Eq. 2 simultaneously for v1f and
v2f gives:
v1f = {(m1 - m2)/(m1
+ m2)} v1i and
v2f = {2m1/(m1 + m2)}
v1i
For v1i = 2.0 m/s, m1 = 1.0 kg
and
- m2 = 1.0 kg, v1f = 0 and
v2f = 2.0 m/s = v1f
Example: Cue ball colliding with another billiard ball.
- m2 = 1000 kg, v1f = - (999/1001)(2.0
m/s) ≈ (1)(2.0 m/s) = - v1i
v2f = (2.0/1001)(2.0 m/s) ≈ 0.004 m/s,
which is small compared to v1i
Example: A basketball colliding with a bowling ball is an
example of a relatively small mass colliding with a large
mass.
- m2 = 0.001 kg, v1f = (0.999)(2.0
m/s) ≈ (1)(2.0 m/s) = v1i
v2f = (2.0/1.001)(1.0 m/s) ≈ 2 v1i
Example: A bowling ball colliding with a basketball is an
example of a relatively large mass colliding with a small
mass.
|
|
|
15.
|
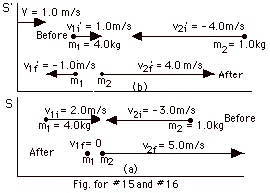
| Momentum is conserved, |
|
|
| |
pi |
= |
pf |
| |
(4.0
kg)(2.0 m/s) + (1.0 kg)(-3.0 m/s) |
= |
(4.0
kg)v1f + (1.0 kg)v2f |
| |
5.0 m/s |
= |
4.0v1f
+ 1.0v2f |
| or |
v2f |
= |
5.0 m/s
- 4.0v1f (Equation
1) |
| |
|
|
|
| Kinetic energy is conserved, |
|
|
| |
Ki |
= |
Kf |
| 1/2(4.0kg)(4.0m2/s2)+1/2(1.0kg)(9.0m2/s2) |
= |
1/2(4.0kg)v1f2+1/2(1.0kg)v2f2 |
| |
1/2 (25)(m/s)2 |
= |
1/2(4.0v1f2+
1.0v2f2) |
| or |
(25)(m/s)2 |
= |
4.0v1f2
+ 1.0v2f2 (Equation
2) |
Substituting Eq. 1 into Eq. 2:
25 (m/s)2 =
4.0v1f2 + (5.0 m/s - 4.0v1f)2
25 (m/s)2 = 4.0v1f2 +
25 (m/s)2 - 40v1f m/s + 16v1f2
0 = 20v1f2 - 40v1f
m/s or
0 = v1f(v1f - 2 m/s)
Solutions are v1f = 0 and
2.0 m/s. To decide which to choose, use Eq. 1.
For v1f = 0, v2f = 5.0 m/s.
For v1f = 2.0 m/s, v2f = - 3.0 m/s.
The latter is not possible because they would collide. The correct
solution is shown in Fig. for 15a.
|
|
|
16.
|

The velocity of the center of mass V = (m1v1i
+ m2v2i)/(m1 + m2) =
{4.0(2.0)+1.0(-3.0)}kg-m/s/5.0 kg = 1.0 m/s.
In the center of mass coordinate system moving with V = 1.0
m/s to the right,
v1i’ = v1i - V = 2.0
m/s - 1.0 m/s = 1.0 m/s.
v2i = v2i - V = -3.0 m/s - 1.0 m/s =
-4.0 m/s.
v1f’ = v1f
- V = - 1.0 m/s = -1.0 m/s.
v2f’ = v2f - V = 5.0 m/s - 1.0
m/s = 4.0 m/s.
Prime velocities are shown in Fig. 16b above.
In center of mass system, pi = (4.0 kg)(1.0 m/s)
+ (1.0 kg)(-4.0 m/s) = 0
= pf = (4.0 kg)(-1.0 m/s) + (1.0 kg)(4.0 m/s). The
center of mass system is a zero momentum system.
|
|
|
17.
|
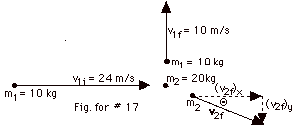
If momentum, a vector quantity, is conserved, its components
are conserved.
(pi)x = (pf)x
10 kg(24 m/s) = (20 kg)(v2f)x
(v2f)x = 12 m/s
(pi)y = (pf)y
0=10 kg(10 m/s)+20 kg (v2f)y
(v2f)y = -5.0 m/s
v2f = {(v2f)x2 +
(v2f)y2}1/2
v2f = (122 + -5.02)1/2
m/s = 13 m/s.
tan Θ= -5/12. Θ
= -22.6o.
|
|
|
18.
|
(pi)x = (pf)x
cos 37o = 0.80 and
sin 37o = 0.60
2.0 kg(39 m/s) = 2.0 kg(v1f)x + 8.0
kg(10 m/s)(0.80)
(78 - 64)m/s = 2.0(v1f)x
(v1f)x = 7.0 m/s
(pi)y = (pf)y
0 = 2.0 kg(v1f)y + 8.0 kg(10 m/s)(0.6)
- 24 m/s = (v1f)y
v1f = {(7.0)2 + (-24)2}1/2
m/s = 25 m/s
tan Θ = - 24/7.
Θ = - 74o.
|
|
|
19.
|
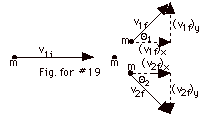
Momentum is conserved
(px)i = (px)f
mv1i = m(v1f)x + m(v2f)x
(Equation
1)
(py)i = (py)f
0 = mv1f sin Θ1
+ mv2f sin Θ2.
Since v1f = v2f,
Θ1 = - Θ2
and
(v1f)x = (v2f)x (Equation
2)
From Eq. 1,
v1i = 2 (v1f)x = 2v1f
cos Θ1 (Equation
3)
From conservation of kinetic energy, Ki = Kf
1/2 m v1i2 = 1/2 m v1f2
+ 1/2 m v2f2 = mv1f2
or
v1f = v2f = v1i/(2)1/2
From Eq. (3), v1i = 2 [v1i/(2)1/2]
cos Θ1; cos
Θ1 = (2)1/2/2
and
Θ1 =45o and Θ2
= - 45o
|
|
|
20.
|
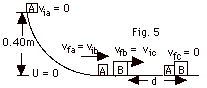
- Take the zero of gravitational potential energy at the
bottom of the ramp, Uaf = 0. At the top
of the ramp, Uai = mgh, where h = 0.40 m.
On the ramp, from conservation of energy
Uai
+
Kai = Uaf + Kaf
mA(9.8 m/s2)(0.40 m) +
0 = 0 + 1/2 mAvfa2
vfa
= [19.6(0.4)]1/2m/s = 2.8 m/s
- When A collides with B, momentum is conserved.
pbi = pbf
mAvib = (mA + mB)vfb
vfb = [mA/(mA + mB)]vib
= [2.0/(11.2)]2.8 m/s = 0.50 m/s
- Work done by friction = (Ucf + Kcf
) - (Uci + Kci)
fd cos 180o =
-(2.8 N)d = (0 + 0) - [0 - 1/2(11.2 kg)(0.50 m/s)2]
-(2.8 N)d = -1.4 N-m and
d = 0.50 m.
|
|
|
21.
|
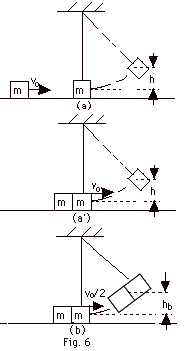
- For an elastic collision in one dimension,
v1f = (m1 - m2)/(m1
+ m2) v1i and
v2f = 2m1/(m1 + m2)
v1i
In this problem, m1 = m2
and v1i = vo. Thus the first
block stops after the collision, v1f =
0, and the second block gains a velocity v2f
= vo (Fig. 6a' above). Now the second block swings
up to height h. Energy is conserved. Taking the middle
of the block as the zero of potential energy at the initial
position i, the potential energy at "final"
position of height h, where the block comes momentarily
to rest is mgh.
Ui + Ki
= Uf
+ Kf
0 + 1/2 mvo2 = mgh +
0
and
h = vo2/2g
- For the inelastic collision,
pi = pf
mvo = 2mvb
vb = vo/2
Uib + Kib
=
Ufb + Kfb
0 + 1/2(2m)(vo2/4)
= 2mgh + 0 and
hb = vo2/8g
|
|
|
22.
|
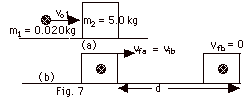
pia
= pfa
0.020 kg(vo1) = (0. 020 + 5.0)kg vaf
vaf
= (0.02/5.02)vo1
It takes 0.80 N to keep the 5.0 kg moving with constant
velocity. The increase in the normal force due to the weight
of the bullet does not change the frictional force to two significant
figures. Take the gravitational potential at the surface = 0
= Ufb = Uib.
Work by friction = (Ufb + Kfb) - (Uib
+ Kib)
-(0.80 N)(1.5 m) = (0 + 0) -
{0 + 1/2(0.502 kg)[0.02vo1/5.02]2}
-1.2 kg(m/s)2 = -3.98 x 10-6
vo12 kg
vo1 = 549 m/s
|
|
|
23.
|
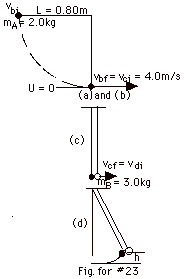
Take the potential energy at the bottom of swing to be zero.
The kinetic energy at the top of the swing is zero since the
velocity of A there vbi = 0.
See the figure for #23 above for parts (a), (b), (c) and (d).
- Ubf + Kbf = Ubi + Kbi
0 + Kbf = (2.0kg)(10 m/s2)(0.80 m)
+ 0
Kbf = 16 J = 1/2(2.0 kg)vbf2
- vbf = 4.0 m/s
- pi = pf
2.0 kg(4.0 m/s) = (2.0 + 3.0)kg vcf
vcf = 1.6 m/s
- Udf + Kdf = Udi + Kdi
5.0 kg(10 m/s2)h + 0 = 0 + 1/2(5.0 kg)(1.6 m/s)2
h = 0.13 m
|
|
|
24.
|
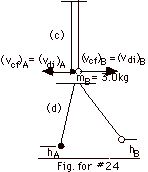
- Parts (a) and (b) above have the same approach as #23
above. The figures for (a) and (b) are the same as for #23
above.
- Parts (a) and (b) above have the same approach as #23
above. The figures for (a) and (b) are the same as for #23
above.
- For the elastic collision,
vBf = 2mA/(mA + mB)(4.0
m/s)= (4/5)(4.0 m/s) = 3.2 m/s.
vAf = (mA - mB)/(mA
+ mB)(4.0 m/s) = (-1.0/5)(4.0 m/s) = -0.8
m/s.
- Udf + Kdf = Udi + Kdi
For B, (3.0 kg)(10 m/s2)hB = 1/2(3.0
kg)(3.2 m/s)2. hB = 0.51 m.
For A, (2.0 kg)(10 m/s2)hA = 1/2(2.0
kg)(-0.8 m/s)2. hA = 0.032 m.
|
|
|
25.
|
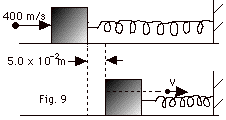
- Do the problem in steps. First there is the collision
between the bullet of mass m = 5.0 x 10-3 kg
travelling with a speed of 400 m/s and the block of mass
M = 1.0 kg. After the collision, the bullet has a
velocity v and the block a velocity vM.
From conservation of momentum,
pi
= pf
(5.0 x 10-3 kg)(400 m/s) = (1.0 kg)vM
+ (5.0 x 10-3 kg)v (Equation
1)
Just after the collision and just before the block compresses
the spring, the initial potential energy of the block-spring
system is 0 and the kinetic energy of the block is 1/2 (1.0
kg) vM2. When the spring has
been compressed to its maximum, the block momentarily comes
to rest and its "final" kinetic energy is zero,
but the potential energy of the block-spring system is 1/2
kx2 = 1/2(900 N/m)((5 x 10-2m)2.
From conservation of energy,
Ui + Ki
=
Uf
+
Kf
0 + 1/2(1.0 kg) vM2 = 1/2(900 N/m)(5.0
x 10-2 m)2 + 0 or
vM = 1.5 m/s
Substituting this value of vM back into Eq. 1:
(5.0 x 10-3 kg)(400m/s) = (1.0kg)(1.5m/s) + (5.0
x10-3 kg)v
or
v = 100 m/s
- For the collision,
Ki = 1/2 (5 x 10-3 kg)(400 m/s)2
= 400 J
Kf = 1/2(5.0 x 10-3 kg)(100 m/s)2
+ 1/2(1.0 kg)(1.5 m/s)2
= (25 + 1.12)J
K lost = (400 - 26.12)J = 374 J
|
|
|
26.
|
This problem is a reminder to choose your system carefully.
When you drop an object, its momentum does not stay constant
because the gravitational attraction of the earth, an external
force, acts on it. If you take your system to be the object
and the earth, then momentum is conserved because the force
of the earth on the object and the force of trhe object on
the earth are internal forces. There is no net external force
on the system of the object and the earth and momentum is
conserved. Let the object be a textbook with mass mb
= 2.0 kg and velocity vb. The earth has a mass
Me = 5.98 x 1024 kg. Before you release
the book, the momentum of the system is zero.
pi = pf
0 = mbvb + Meve,
where ve = the speed acquired by the earth.
ve = (mb/Me)vb
= (2.0 kg/5.98 x 1024 kg)vb = 3.3 x 10-25
vb.
So the earth does move up, but we do not detect the motion.
|
|