|
|
|
1.
|
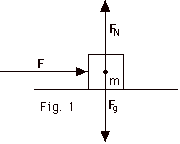
We again use the Principle of Superposition to solve this
problem by separating the problem into forces acting along
the horizontal or X-axis and those acting along the vertical
or Y-axis. Then, for each axis, all forces will be along a
line. We assign a positive or negative sign to the forces,
depending on their direction along the axis, and then add
them algebraically. There is no acceleration in the Y-direction,
ay = 0. (Fnet)y =
may =m(0) = 0
(a) and (b),
FN - Fg = 0 or
FN = Fg = mg .
For m = 2.0 kg, FN = Fg = (2.0 kg)(10
m/s2) = 20 N.
(Fnet)x = max
F = max or
ax = F/m
For (c) ax = 12 N/ 2.0 kg = 6.0 m/s2.
For (d) ax = 24 N/2.0 kg = 12.0 m/s2.
The acceleration is directly proportional to the net force.
When you double the net force, you double the acceleration.
For (e) ax = 12 N/1.0 kg = 12.0 m/s2.
The acceleration is inversely proportional to the mass of
the object. When you halve the mass, you double the acceleration.
|
|
|
2.
|
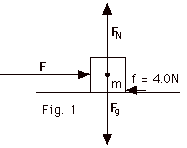
Now the net force in the X-direction depends on an applied
force to the right and a frictional force to the left.
(Fnet)x = max
F - f = max
- 12 N - 4 N = 2.0 kg ax
4.0 m/s2 = ax
- 24 N - 4 N = 2.0 kg ax
10 m/s2 = ax
While the applied force F is doubled, the net force is
not doubled and the acceleration is not doubled. The second
net force = 20/8 x the first net force = 5/2 the first
net force. The second acceleration = 5/2 the first acceleration
= 5/2 x 4.0 m/s2 = 10 m/s2.
|
|
|
3.
|
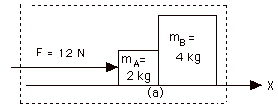
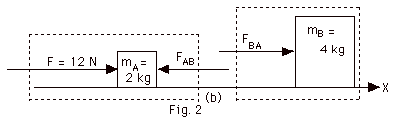
In Fig. 2a above, I have isolated (shown by dashed box) the
entire system in order to find the acceleration of the two blocks.
In Fig. 2b above, I have isolated A and B separately in order
to find FAB and FBA. FAB
is the force of B on A and FBA is the force of A
on B. FAB is an external force to the system
which consists only of A and FBA is an external force
to the system which consists only of B. FAB
and FBA are internal forces to the system of Fig.
2a. I do not use a Y-axis in the figures because I am
not interested in the normal forces and there is no friction
in the problem. For the entire system of Fig. 2a, I know the
external force that acts on it along the X-axis and I know the
mass of the system so I can find its acceleration. Since I am
interested only in the X-direction, I drop the subscript x on
Fnet and a.
(a) Fnet external = (mass of system)a
12
N = (2 + 4)kg (a) or
12
N/6 kg = 2 m/s2 = a
Now we isolate block A to find FAB since we know
mA and a and then isolate block B because we know
everything but FBA, as shown in Fig. 2b. F
is only in contact with A and A pushes B to the right, while
B pushes A to the left.
| |
For
block A |
|
For
block B |
| (b) |
(Fnet external)on
A = (mA)a |
(c) |
(Fnet external)on
B = (mB)a |
| |
F - FAB =
(2 kg)(2 m/s2) |
|
FBA = (4
kg)(2 m/s2) |
| |
12 N - FAB =
4 N |
|
FBA = 8 N |
| |
or
12 N - 4 N = 8 N = FAB |
|
|
FAB and FBA
are Newton third law of motion forces. They are equal
in magnitude, but opposite in direction. FAB,
the force of B on A, has a magnitude of 8 N and is to the left.
FBA, the force of A on B, has a magnitude
of 8 N and is to the right.
|
|
|
4.
|
It is a little difficult to solve (a) of this problem without
a sneak look at the figure for part (b). There are a lot of
forces here, but Fig. 3-4a below shows the only external
force in the horizontal direction acting on the system of
the two blocks. Again Fnet external = ma, where
a is the acceleration of the blocks and m is the mass of the
system we have isolated. There are internal forces acting
in the system, for example, the force of the rope on A, FAR,
the force of the rope on B, FBR. And we cannot
forget the force of A on the rope, FRA, or the
force of B on the rope, FRB. I have not drawn the
vectors for the gravitational forces on the blocks or the
normal force of the surface on the blocks because they were
not asked for and there is no frictional force.
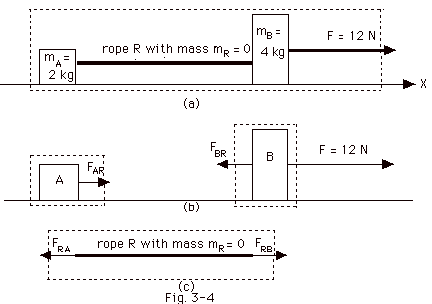
While Figures 3-4b and c above show forces FAR,
FBR, FRA and FRB,
these are internal to the system shown in Fig. 3-4a
above. The only external force for the entire system
in the horizontal direction is F = 12 N.
- Thus for the system shown in Fig. 3-4a above,
(Fnet external)x = (mass
of system)a
12 N = (2 + 4)kg (a) or
12 N/6 kg = 2 m/s2 = a
For part (b), let us stare at Fig. 3-4b and c, which I reproduce
below:
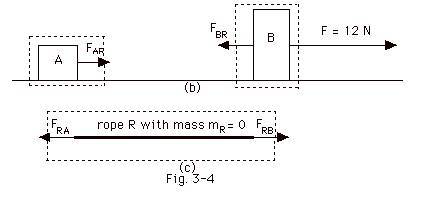
Let's cope with the massless rope first:
(Fnet external)on rope
= (mR)a
Taking to the right to be positive,
FRB - FRA = (0)a, where
a = the acceleration of the rope
So,
FRB = FRA
It is important to notice that FRB and
FRA, while equal and in opposite directions,
are not Newton third law of motion forces because
they act on the SAME object. They are equal and in
the opposite direction because they must sum to zero because
a massless object has no net force acting on it. Then by
Newton's third law we know that:
FRA = - FAR and
FRB = -FBR.
Thus since the magnitudes of these forces are equal, FRA
= FRB, FAR = FBR.
We throw all this careful notation to the wind and call
FAR, FBR, FRA and FRB
the tension T. With this information we redraw Fig. 3-4b
below:
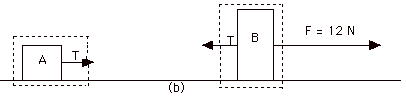
- Now we can choose either object to find the tension T
in the rope. You can check the answer by isolating the other
block and finding T.
| For block B, in
the X-direction, |
For block A, in
the X-direction, |
| (Fnet external)x
= (mB)a |
(Fnet external)x
= (mA)a |
| 12 N - T = (4 kg)(2 m/s2)
= 8 N |
T = (2 kg)(2 m/s2)
= 4 N |
| So
12 N - 8 N = T = 4 N |
|
|
|
|
5.
|
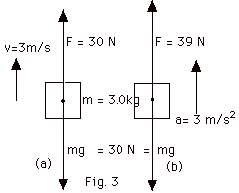
The forces acting on the object are the applied force F and
the weight of the object mg. In all cases, Fnet =
ma
(a) For constant velocity, a = 0 and F - mg = m(0) = 0
or
F = mg = 3.0 kg (10 m/s2) = 30 N
(b) For a constant acceleration, a = 3.0 m/s2,
F - 30 N = 3.0 kg(3m/s2)
or
F = 9.0 N + 30 N = 39 N.
|
|
|
6.
|
- For entire system (Fig. 4a above),
Fnet = Ma
F - 3mg = (3m)a
9.0 N - (0.30kg)(10 m/s2) = (0.30 kg)a
9.0 N - 3.0 N = (0.30 kg)a
20 m/s2 = a
- To find the tension at the top of the rope T(b) first
use the lower figure in Fig. 4b above.
Fnet = Ma
T(b) - 2mg = (2m)a
T(b) - 2.0 N = (0.20 kg)(20m/s2)
T(b) - 2.0 N = 4.0 N.
T(b) = 6.0 N
Check with top figure in Fig. 4b above.
Fnet = Ma
9.0 N - mg - T(b) = ma
9.0 N -1.0 N - T(b)=(0.10 kg)(20 m/s2)=2.0 N
6.0 N = T(b)
- The mass of 1/5 of the rope = m/5 = 0.02 kg and its weight=mg/5=
0.2N. Use the top figure in Fig. 4c above.
Fnet = Ma
9.0 N - 1.2 mg - T(c) = (0.12 kg)(20 m/s2) =
2.4 N
T(c) = 5.4 N
Using the bottom figure in Fig. 4c above,
T(c) - 1.8 mg = T(c) - 1.8 N = (0.18 kg)(20 m/s2)
= 3.6 N
T(c) = 5.4 N
|
|
|
7.
|
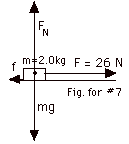
| (Fnet)x
= max |
(Fnet)y
= may |
| 26 N - f = 2.0 kg(ax) |
FN - mg = m(0) |
| |
FN = mg = (2.0 kg)(10m/s2)=20N |
- f
= µkFN = 1/5(20 N) = 4.0 N
26 N - 4.0 N = 2.0 kg(ax)
- 11 m/s2 = ax
|
|
|
8.
|
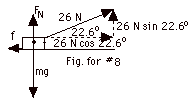
- (Fnet)y = may
FN + 26 N sin 22.60 -
mg = 0
FN = + 20 N - 26 N(5/13) = 20 N - 10 N = 10 N.
f = µkFN = (1/5)(10
N) = 2 N
- (Fnet)x = max
26 N cos 22.60 - f = 2.0 kg(ax)
26 N(12/13) - 2 N = 2.0 kg(ax)
24 N - 2 N = 2.0 kg(ax)
11 m/s2 = ax
|
|
|
9.
|
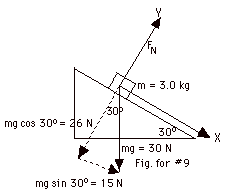
(a) & (b) The x-axis is chosen in the direction of the
acceleration. The axes, forces and components of forces
are shown in the figure above.
(c) (Fnet)x = max
30 N sin 300 = 3.0 kg(ax)
15 N = 3.0 kg(ax)
5.0 m/s2 = ax
|
|
|
10.
|
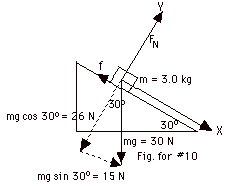
- Now there is a frictional force up the plane.
(Fnet)y = may
FN - mg cos 30o =
0
FN = 30 N (0.866) = 26 N
f = µk FN = 0.154(26 N) = 4.0
N
- (Fnet)x = max
30 N sin 30o - f = 3.0 kg(ax)
15 N - 4.0 N = 3.0 kg(ax)
ax = 11/3m/s2
|
|
|
11.
|
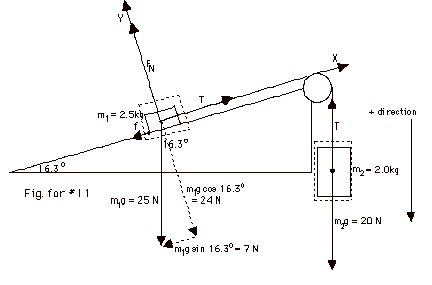
- First isolate m1, taking the X-axis in
the direction of the acceleration:
| (Fnet)x
= m1ax |
(Fnet)y
= m1ay |
| T - m1g
sin 16.3o - f = m1ax |
FN -
m1g cos16.3o = m1(0) |
| |
FN =
25 N(24/25) = 24 N
f = µkFN = 1/6(24 N) =
4 N |
| T - 25 N(7/25) -
4 N = 2.5 kg a |
|
| T - 11 N = 2.5 kg
a (Equation
1) |
| Note:
I have dropped the subscript on a, the only acceleration. |
Now isolate m2,
taking down as positive:
Fnet = m2a
m2g - T = m2a
20 N - T = 2.0 kg a (Equation
2)
Adding Eq. 1 and Eq. 2:
20 N - 11 N = 4.5
kg a or
a = 2.0 m/s2
- Substituting a = 2.0 m/s2
into Eq. 2:
20 N - T = 2.0 kg(2.0
m/s2) and
T = 16 N.
|
|
|
12.
|
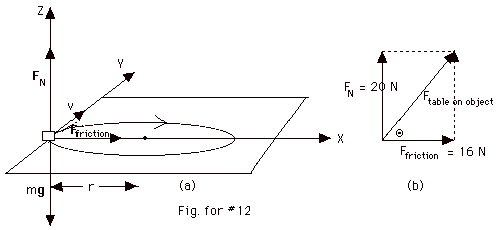
Figure for #12a above is a sketch of the object moving on the
table and all of the forces acting on it. As the object starts
to slip away from the circle, a frictional force acts into the
center of the circle to produce the centripetal acceleration.
I chose the X-axis to the right because at the moment shown
in the picture, the centripetal acceleration is into the center
of the circle or to the right. The frictional force is the only
force into the circle or, as I have drawn it, along the positive
X-axis. This is a three dimensional drawing showing that for
clockwise motion, at this instant of time, the velocity is along
the positive Y-axis. The weight of the object is always along
the negative Z-axis and the normal force of the table along
the positive Z-axis. Now our axis of interests are the X-axis
and the Z-axis. The acceleration in the positive X-direction
is the centripetal acceleration = v2/r.
- (Fnet external)x = max
Ffriction = mv2/r = 2 kg (2 m/s)2/(0.5
m) = 16 N
- There is no acceleration in the Z-direction.
(Fnet external)z = maz.
FN - mg = m(0) or
FN = mg = (2 kg)(10 m/s2) = 20 N
As shown in Fig. for #12b above,
Force of table on object = {(Ffriction)2
+ FN2)1/2
= {(16)2 + (20)2}1/2
N
= {656}1/2 N = 25.6 N
tan Θ = FN/Ffriction
= 20/16 = 1.25
Θ = 51.3o
|
|
|
13.
|
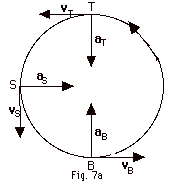
- The centripetal acceleration a = v2/r = (3m/s)2/0.5
m = 18 m/s2. The object travels in a counterclockwise
direction so the directions of the velocities are as shown
in Fig. 7a above. Remember the velocity is always tangent
to the path. Thus,
- at B the velocity is to the right,
- at T the velocity is to the left, and
- at S the velocity is down.
- At B the acceleration is into the center of the circle
or up. At B we take the X-axis up.
- At T the acceleration is into the circle or down. At T
the X-axis is down.
- At S the acceleration is to the right and the X-axis is
to the right. All of the accelerations are in the direction
of the net force.
For all cases Fnet = ma = 2 kg(18 m/s2)
= 36 N.
Looking at Fig. 7b below, we see that at B and T, there
are no components of the force in any direction except the
X-direction so we drop the subscripts on Fnet.
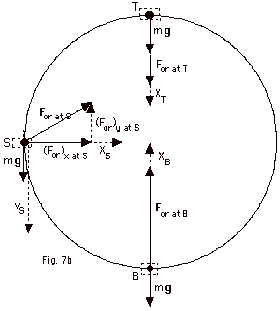
- At B,
Fnet = ma
For at B - mg = ma
For at B - 20 N = 36 N
For at B = 56 N
- At T, I have drawn For at T down, but I must
use the equation for a final decision, so I write it with
± to find its sign and, therefore, its direction.
Fnet = ma
±For at T + 20 N = 36 N so
For at T = +16 N or it is down.
- At S, For at S must have
a component into the center or along the +X-axis to produce
the centripetal acceleration and a component along the +Y-axis
so the net force along the Y-axis is zero keeping the magnitude
of the velocity for the uniform circular motion constant.
Thus, we must look at Fnet along the X and Y-axes.
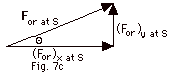
| (Fnet)x
at S = max |
(Fnet)y
at S = may |
| (For)x
at S = 36 N |
(For)y
at S - mg = m(0)
(For)y at S = mg = 20 N |
| For
at S = {(For)2x at
S + (For)2x at S}1/2 |
| For
at S = {(36)2 + (20)2}1/2
N = 41 N |
|
tan
Θ = (For)y/(For)x
= 20 N/ 36 N = 0.55.
Θ = 29o |
|
|
|
14.
|
- Forces shown in Fig. 8 below:
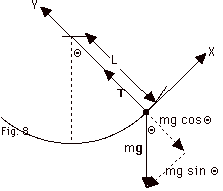
- (Fnet)x = max
(Fnet)y = may
-mg sin Θ= max
T - mg cos Θ=
mv2/L
Acceleration in the X-direction = -g sin Θ
Acceleration in the Y-direction = v2/L, where
v is speed of the object at that instant and L is the radius
of the circular arc.
ay = v2/L = T/m - g cos Θ
- In general, ax = -g sin Θ
(i) at maximum displacement, ax
= -g sin Θmax
(ii) at the equilibrium position, Θ
= 0, sin Θ= 0, ax
= 0.
In general, T- mg cos Θ=mv2/L.
- At its maximum displacement, the bob comes momentarily
to rest,
v = 0 and T = mg cos Θmax.
- At the equilibrium position, v = vmax,
T = mg cos 00 + mvmax2/L
= mg + mvmax2/L.
|
|
|
15.
|
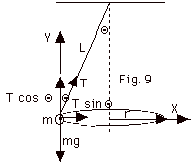
The forces acting on the object are its weight mg
and the tension T in the string. The acceleration
is into the center or, at this instant, to the right. We
take the X-axis in the direction of the acceleration and
the Y-axis perpendicular to it. The weight mg is
in the negative Y-direction, but T is in neither
the X nor Y direction so we take components, as is shown
in Figure 9 above. The acceleration in the X-direction
is the centripetal acceleration v2/r. There is
no acceleration in the Y-direction.
| (Fnet)x
= max |
(Fnet)y =
may |
| T sin Θ
= mv2/r (Equation
1) |
T cos Θ
- mg = 0 or
|
| |
T cos Θ
= mg (Equation
2) |
Dividing Eq. 1 by Eq. 2:
T sin Θ/T
cos Θ = tan Θ
= (mv2/r)/(mg) = v2/rg (Equation
3)
From geometry, we see that r/L
= sin Θ or
r = L sin Θ
(Equation
4)
- Substituting Eq. 4 into Eq.
3:
tan Θ= v2/(L
sin Θ)g or
(tan Θ) (L sin
Θ)g= v2 and
v =(Lg sin Θtan Θ)1/2
- v = (distance traveled/time)
= 2πr/T or
T= 2πr/v = 2 π(L
sin Θ)/v =
T = 2 π(L sin Θ)/(Lg
sin Θtan Θ)1/2
= 2 π(L
sin Θ)/(Lg sin2Θ/cos
Θ)1/2 =
T = 2 π(L cos Θ/g)1/2
|
|
|
16.
|
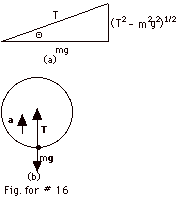
- For motion in a horizontal circle, from the solution
to #15, we see that:
T sin Θ= mv2/L
sinΘ or
v2 = TL sin2 Θ/m
(1)
Also, T cos Θ= mg
or
cos Θ= mg/T
From Fig. a, we see that:
sin Θ= (T2
- m2g2)1/2/T (2)
Substituting Eq. 2 into Eq. (1):
v2 = TL/m (T2 - m2g2)/T2
= TL/m {1 - (mg/T)2}
or
v = (TL/m)1/2 {1 - (mg/T)2}1/2
- For a vertical circle, maximum tension occurs when the
object is at the lowest point and the tension and weight
of the object are in opposite directions. For this case,
T - mg = mv2/L or
v ={(T - mg)L/m}1/2
|
|
|
17.
|
- Plots of the position in the x and y direction as a function
of time are straight lines. The slopes of these lines are
the constant velocities, vx and vy,
respectively. For constant velocity, there is no acceleration
nor force. Fx = 0. Fy =
0.
- For the projectile, the object travels equal horizontal
distances in equal time with a constant velocity. Fx
= 0. There is a constant acceleration down. Fy
= - constant.
- The speed of the particle is constant. The velocity is
always tangent to the circle. This is uniform circular motion
with the acceleration in toward the center. It is constant
in magnitude, but changes direction.
Fx = - (constant)x and
Fy = - (constant)y.
F = Fxi + Fyj = - (constant)(xi
+ yj) or
F = - (constant)r, where r is
a radial vector.
- The slope of vx versus t = k = ax.
The slope of vy versus t = -k’ = ay,
where k and k’ are constants.
Fx = c and Fy =
-c’, where c and c’ are new constants.
|
|
|
18.
|
(b)
(a) First isolate the entire system as shown in Fig. 11a
above. For this system, T2, T3,
the force Fmp of the platform on the man,
and the force Fpm of the man on the platform are
internal forces. The external forces are T1, the
weight of the man (mg)man, and the weight of the
platform (mg)platform.
Fnet external = Ma
T1 -1000 N - 600 N = (100 + 60)kg (5.0 m/s2)
T1 = 2400 N
T2 = T3 = T1/2 = 1200 N
(c) Now isolate the man as shown in Fig. 11b above:
Fnet external = mman a
T3 - (mg)man + Fmp = 100
kg (5 m/s2)
1200 N - 1000 N + Fmp = 500 N
The force of the platform on the man Fmp = 300
N.
As a check, let us isolate the platform, as in Fig. 11c above:
Fnet external = mplatform a
T2 - (mg)platform - Fpm =
60 kg (5 m/s2)
1200 N - 600 N - Fmp = 300 N
Force of the man on the platform Fpm = 300 N.
Fmp and Fpm are Newton third law
of motion forces. They are equal in magnitude and opposite
in direction.
|
|
|
19.
|
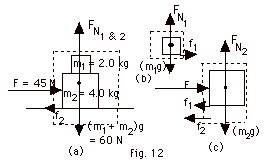
First isolate the entire system (Fig. 12a above). For the entire
system, the external forces are the applied force F, the frictional
force f2 of the surface on m2, the
normal force FN on 1 & 2 of the surface on the two
blocks and the attraction of the earth for the objects or the
weight of the objects, (m1 + m2)g.
As the objects move to the right, f2 acts
to the left.
| (Fnet)x
= Max |
(Fnet)y
= May |
| 45 N - f2
= 6.0 kg a |
FN on 1 & 2 -
60 N = 0
FN on 1 & 2 = 60 N |
|
f2 = µk FN on 1 & 2
= 0.25(60 N) = 15 N |
| 45 N - 15 N = 6.0 kg
a |
|
| 5.0 m/s2
= a |
|
Now isolate m1 (Fig. 12b
above). There must be a frictional force f1 on
m1 due to m2 to
the right to produce the acceleration of m1.
| (Fnet)x
= m1ax |
(Fnet)y
= m1ay |
| f1
= 2.0 kg(5 m/s2) |
FN1
- 20 N = 0
FN1 = 20 N and
f1 = µs(20 N) |
µs(20
N) = 10 N
µs = 1/2 |
|
As a check isolate m2
(Fig. 12c above). By Newton's third law, m1 must
exert a force f1 on m2
to the left.
(Fnet)x = m2ax
45 N - f2 - f1 = 4.0 kg(5 m/s2)
or
45 N - 15 N - f1 = 20 N
and again,
f1 =10 N with
µs(20 N) = 10 N and
µs = 1/2.
|
|
|
20.
|
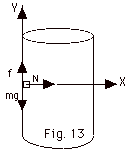
As the block starts to slip down, a frictional force f opposes
the motion.
| |
(Fnet)x
= max |
(Fnet)y
= may |
| |
N
= mv2/R |
f - mg = 0 or
f = mg = µsN |
| Since |
v
= 2 πR/To
= 2 πRfo |
N = mg/µs
(Equation
1) |
| |
N
= m(4 π2R2fo2)/R |
(Equation
2) |
Substituting Eq. 1 into Eq. 2 gives:
fo = (1/2 π)(g/µsR)1/2
|
|
|
21.
|
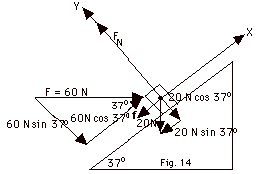
Take the X-axis in the direction of the acceleration or up the
plane and the
Y-axis perpendicular to it (Fig. 14 above).
(Fnet)x max
F cos 37o - mg sin 37o - f = ma
60 N(4/5) - 20 N(3/5) - f = 2.0 kg(a)
48 N - 12 N - f = 0
(Equation
1)
(Fnet)y = may
FN - F sin 37o - mg cos 37o
= m(0)
FN = 60 N(3/5) + 20 N(4/5) = 52 N
f = µkFN = 1/2(52 N)
= 26 N (Equation
2)
Substituting Eq. 2 into Eq. 1:
48 N - 12 N - 26 N = 2.0 kg(a) or
a = 5.0 m/s2
|
|
|
22.
|
- Net force on sled = msledasled =
10 kg(2.0 m/s2) = 20 N = force of man on sled.
- By Newton's third law, force of man on sled = force of
sled on man
= 20 N.
- Net force on man = mmanaman = 60
kg(2.0 m/s2) = 120 N = frictional force of snow
on man - force of sled on man. 120 N = frictional force
of snow on man - 20 N. Frictional force of snow
on man = 140 N.
|
|
|
23.
|
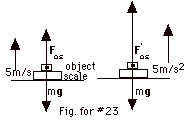
- Let Fos = the force of the scale on the object
when the elevator moves with a constant velocity. For
constant velocity, Fnet = ma = m(0).
Fos - mg = 0, and Fos = mg =
(10 kg)(10 m/s2) = 100 N. By Newton's third
law, the force of the scale on the object = the force of
the object on the scale. The reading of the scale is 100
N.
- Let F'os = the force of the scale on the object
when the elevator moves upward with a constant acceleration
of 5 m/s2.
Fnet = ma = (10 kg)(5 m/s2).
F'os - mg = 50 N, or F'os =
50 N + 100 N = 150 N.
F'os = F'so = reading of scale = 150
N.
|
|
|
24.
|
Fnet = mg - f = ma or a =
g - f/m. The lead sphere has a greater density than the wood
sphere. The volume of the spheres = 4/3 πr3
and the mass m of the spheres = density x volume. The lead sphere
has the same volume as the wood sphere since their radii are
identical, but it has a larger mass because it has a greater
density. Since a = g - f/m, the sphere of the larger mass has
the greater acceleration.
|
|
|