|
|
|
1.
|
(a) From Figures 1a and 1b above, we
find the wavelength to be 4.00 cm.
(b) The crest at x = 1.00 cm in Fig. 1a moves to x = 3.00
cm in Fig. 1b in 10 s. Since the wave moves one wavelength
in a period T and (3.00 cm - 1.00 cm) is one-half wavelength,
the period is 20 s. The frequency f = 1/T = (1/20) s-1.
(c) v = f λ = (1/20) s-1
(4.00 cm) = 0.20 cm/s.
(d) At t = 10 s, there is a crest at x = 3.00 cm. There will
be two more crests at 3.00 cm + λ
and 3.00 cm + 2 λ or at
x = 7.00 cm and x = 11.00 cm.
(e) At t = 0 there is a crest at x =1.00 cm. There will be
another crest at T =
20 s.
(f) The rope has zero displacement at any x twice each period.
(g) There is one crest at any point in one period. In 80 s
there will be 80/20 =
4 crests.
|
|
|
2.
|
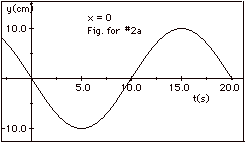
(a) In Fig. 1a above, for y = 0
at t = 0 and x = 0, you see a trough approaching
from the left. Similarly in Fig. 1b, for y = 0
at t = 10 s and x = 0, you see a crest approaching
from the left. This is shown below in a plot of y as a function
of t for x = 0 (Fig. for #2a):
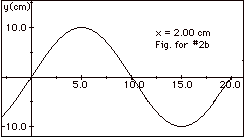
(b) In Fig. 1a above, for y = 0 at t = 0
and x = 2.00 cm, you see a crest approaching from
the left. A plot of y as a function of t for x = 2 cm is shown
in Fig. for #2b below:
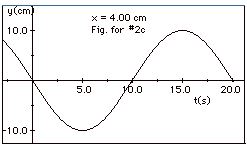
(c) In Fig. 1a, for y = 0 at t = 0
and x = 4 cm, you see a trough approaching from the
left. In Fig. 1b, for y = 0 at t = 10 s
and x = 4 cm, you see a crest approaching from the left.
A plot of y as a function of t for x = 4.0 cm is shown in
fig. for #2c below:
|
|
|
3.
|
The question is answered simply by looking
at Fig. for #2a through #2c above.There is no question that
Fig. for #2a is equivalent to #2c. Points are in phase when
they are an integral number of λ's
apart. Points at x = 0 and x =
2 cm are λ/2 apart and
are 180o out of phase. Points at x = 0 and x =
4 cm are λapart and are
in phase.
|
|
|
4.
|
For a wave traveling to the
right, we may write
y(x,t) = ym sin (2 πx/
λ - 2πt/T)
where ym is the amplitude of the wave, λ
its wavelength, and T the period.
For this case ym = 10 cm, λ
= 4.0 cm, T = 20 s, and
y(x,t) = 10 cm sin [(2 πx/4.0)cm-1
- (2 πt/20)s-1]
= 10
cm sin [( πx/2)cm-1
- (0.1 πt)s-1]
|
|
|
5.
|
(a) For x = 0,
y(0,t) = 10 cm sin (-0.1πt
s-1)
= -10 cm
sin (0.1πt
s-1)
as shown in Fig. for #2a above.
(b) For x = 2.0 cm,
y(2.0 cm, t) = 10 cm sin [(2π/2)
- (0.1πt)s-1]
=
10 cm{ sin π
cos 0.1πt
s-1 - cos π
sin 0.1πt
s-1}
=
10 cm{(0) cos 0.1πt
s-1 - (-1) sin 0.1πt
s-1}
=
10 cm sin 0.1πt
s-1
as shown in Fig. for #2b above.
(c) For x = 4.0 cm,
y(4.0 cm, t) = 10 cm sin [(4π/2)
- (0.1πt)s-1]
=
10 cm{ sin 2π
cos 0.1πt
s-1 - cos 2πsin
0.1πt
s-1}
=
10 cm{(0) cos 0.1πt
s-1 - (1) sin 0.1πt
s-1}
=
-10 cm sin 0.1πt
s-1
as shown in Fig. for #2c above.
|
|
|
6.
|
For x = 0, y(0,t) = -10 cm sin (0.1 πt
s-1):
(a) v(0, t) = dx/dt = -1.0 π
cm/s cos (0.1πt s-1)
(b) a(0,t) = dv/dt = +0.1π2
cm/s2 sin (0.1 πt
s-1) = -(0.1π2
s-2)y(0,t)
|
|
|
7.
|
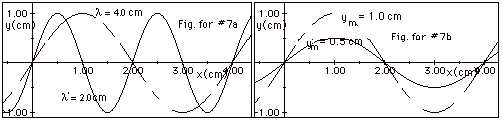
Dashed
wave: λ = 4.0 cm: solid: λ’
= 2.0 cm.
Dashed wave: ym = 1.0 cm; solid: ym’
= 0.5 cm
(a) Two waves of the same amplitude, but different wavelengths
(Fig. for #7a).
(b) Two waves of the same wavelength, but different amplitudes
(Fig. for #7b).
|
|
|
8.
|
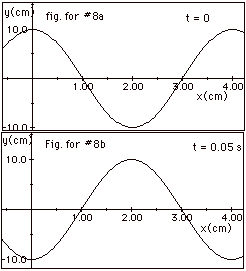
Since y has a maximum displacement of 10 cm at x = 0, we use
a cosine function for the wave of amplitude xm =
10 cm. With a frequency f of 10 s-1 and a velocity
v = 40 cm/s, λ = v/f
= 40 cm/s/10 s-1 = 4.0 cm.
(a) A plot of y as a function of x for t = 0 is shown in Fig.
for #8a above. Notice the maximum displacement of 10 cm for
x = 0 and the wavelength of the wave as 4.0 cm.
(b) For f = 10 s-1, T = 1/f = 0.10 s. A plot of y
as a function of x for t = 0.05 s
= T/2 is shown in Fig. for #8b above. Notice that the crest
at x = 0 for t = 0 has moved to x = 2.0 cm = λ/2
in time T/2. In general for a wave moving to the right,
y(x,t) = ym cos(2 πx/ λ
- 2πt/T)
For this wave,
y(x,t) = 10 cm cos [( πx/2)cm-1
- (20 πt)s-1]
|
|
|
9.
|
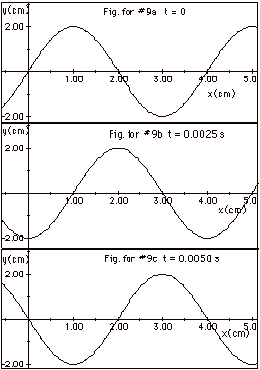
(a) In general, y(x,t) = ym sin (2 πx/ λ
- 2πt/t)
for a wave to the right. For our case, y(x,t) = 2.0 cm sin (0.50 π
cm-1x - 200 π
s-1t). By comparison, ym = 2.0 cm; 2π/ λ
= 0.50 π cm-1,
or λ = 4.0 cm; 2 π/T
= 200 π s-1, or
T = 0.01 s; frequency f = 1/T = 100 s-1; v = λf
= (4.0 cm)(100 s-1) = 40 cm/s; direction of the wave
is to the right because of - sign in wave equation.
(b) There is a crest at x =1.00 cm at t = 0 (Fig. for #9a above).
This crest moves to the right to x = 2.00 cm or a distance of
1.00 cm = λ/4 in time 0.0025s
= T/4 (Fig. for #9b above). The crests moves to the right to
x = 3.00 cm or a distance of 2.00 cm = λ/2
in time 0.0050 s = T/2 (Fig. for #9c above).
(c) y(x, t) = 2.0 cm sin(0.5 π
cm-1x-200 πs-1t).
(dy/dt)x =1cm = -400 π
cm/s cos(0.5 π -200 πs-1t).
(dy/dt)x=1cm,t=0 = -400 π
cm/s cos 0.5π
= 0.
(dy/dt)x=1cm,t = 0.0025s = -400 π
cm/s cos(0.5 π - 0.5 π)
= -400 π cm/s.
|
|
|
10.
|
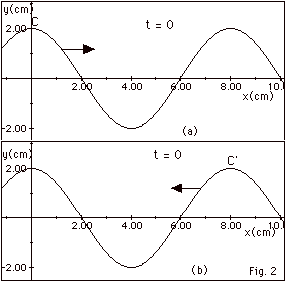
A wave moves one wavelength in one period. From Figs. 2a and
2b above, we see that the wavelength of the waves = 8.0 cm
. In one-half period the waves moves 4.0 cm. Crest C, on the
wave that is moving to the right, at x = 0 in Fig. 2a, moves
to x = 4.0 cm in T/2. Crest C’, on the wave that is
moving to the left, at x = 8.0 cm in Fig. 2b, moves to x =
4.0 cm. At t = T/2, there will be a double crest at x = 4.0
cm with a displacement y = 4.00 cm.
The individual waves to the right and
to the left, respectively, are shown immediately above in
Fig for #10 (b) at t = 3T/4. Now C has moved to the right
3 λ/4 = 6.0 cm to x = 6.0
cm and C’ has moved 6.0 cm to the left to x = 2.0 cm.
C at x = 6.0 cm is superimposed with a trough at this point
from the wave moving to the left. C’ at x = 2.0
cm is superimposed with a trough at this point from the wave
moving to the right. The entire string has zero displacement
at
t = 3T/4.
|
|
|
11.
|
(a) Points on a rope along which a traveling
wave exists vibrate up and down with simple harmonic motion.
(b) All point on the rope except the nodal points on a rope
along which a standing wave exists vibrate up and down with
simple harmonic motion.
(c) All points on a rope along which a traveling wave exits
vibrate with the same amplitude.
(d) The amplitude of a rope along which a standing wave exists
varies from a maximum at the antinodes to zero at the nodes.
(e) The entire rope along which a traveling wave exits never
has zero displacement.
(f) The entire rope along which a standing wave exists has
zero displacement twice each period.
|
|
|
12.
|
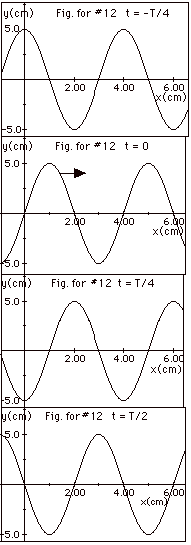
The plots are shown in Fig. for #12 below
for a wave traveling to the right.
The wavelength of the wave is 4.0 cm. The crest at x = 0 at
-T/4 moves to
x = 1.0 cm at t = 0; to x = 2.0 cm at t = T/4, and to x =
3.0 cm at t = T/2.
|
|
|
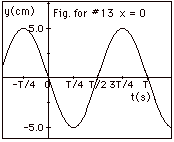
13.
|
|
The plot of y vs t for x = 0 is
shown to the right in Fig for #13. If you look above
at the graphs for Fig. for #12, you see that the point
at x = 0 has the following values of y:
y = 5.0 cm at t =-T/4, y = 0 at t = 0,
y = 5.0 cm at t = T/4, and y = 0 at t = T/2.
|
 |
|
|
|
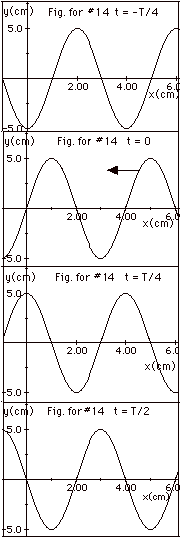
14.
|
The plots are shown in the graphs below
in Fig. for #14 for a wave traveling to the left. The crest
at x = 6 cm at t = -T/4 moves λ/4
= 1 cm to x = 5 cm at t = 0; to x = 4 cm at x = T/4, and to
x = 3 cm at x = T/2.
|
|
|
15.
|
If you look back at the graphs for Fig.
for #12 and Fig. for #14, above, and add the displacement
y for various values of x for t = -T/4, t = 0, t = T/4, and
t = T/2, you will get the graphs shown below in Fig. for #15.
At times t = -T/4 and
t = T/4, the entire rope has zero displacement.
|
|
|
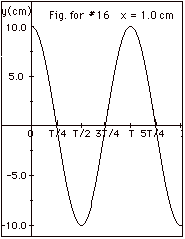
16.
|
The point on the rope at x = 1.0 cm is
an antinodal point. If you look above at the Fig. for
#15 you see the point at x = 1.0 cm has y = 10 cm at t = 0,
y = 0 at t = T/4, and y = -10 cm at T/2. These correspond
to the values of y as a function of time shown in the Fig.
for #16 below. The amplitude of an antinodal point varies
from 0 to a maximum, in this case, 10 cm.
|
|
|
17.
|
(a) The unit of force is N or kg-m/s2.
The unit of mass per unit length µ is kg/m, the unit of
velocity v is m/s.
- The unit of µ/F is (kg/m)/(kg-m/s2) =
(s/m)2 ≠ m/s.
- The unit of F/µ is (kg-m/s2)/(kg/m) =
(m/s)2 ≠ m/s. We could stop here and write
down the answer, but let's carry on.
- The unit of (µ/F)1/2 = s/m ≠ m/s.
- The unit of (F/µ)1/2 = m/s!
(b) The distance between nodes is λ/2.
Thus the number of nodes is inverserly proportional to λ.
λf = v. The velocity
v is directly proportional to the square root of the tension
F. If the tension is increased by a factor of four, the square
root of the tension and the velocity is increased by a factor
of two. For a fixed frequency f, the wavelength is directly
proportional to the velocity v. If the velocity is doubled,
the wavelength is doubled. If the wavelength is doubled, the
number of nodes, which is inversely proportional to the wavelength,
is halved. |
|
|
18.
|
In general for a wave to the left, y(x,t)
= ym sin (2 πx/ λ
- 2πt/T). When we compare
y(x,t) = 2.0 cm sin (2πx
cm-1 - 600πt
s-1), you see that 2 π/λ
=
2 π cm-1, or
λ= 1.0 cm. Also
2 π/T = 600 π
s-1, or T = (1/300) s and
f= 1/T = 300 s-1.
(a) v = λf = 1.0 cm(300
s-1) = 300 cm/s.
(b) v = (F/µ)1/2, or v2 =
F/µ.
µ = F/v2 = 18 N/(3 X 102
m/s)2 = 2 x 10-4 (kg-m/s2/m2/s2)
= 2 x 10-4 kg/m.
|
|
|
19.
|
To find the equation of a wave, we must
find the amplitude A, wavelength λ,
and frequency f of the wave. We are given ym =
1.0 cm and f = 100 s-1, the tension in the
string F = 1.6 N, the mass per unit length µ =
4.0 x 10-3 kg/m. We know that λ
= v/f and v = (F/µ)1/2 = (1.6 N/4.0 x10-3
kg/m)1/2 = 20 m/s. Then λ
= v/f = 20 m/s/100 s-1 = 0.20 m = 20 cm. The
wave is going toward smaller values of x, or to the left.
For a wave to the left, y(x,t) = ym sin (2πx/ λ
+ 2 πft).
For our case, y(x,t) = 1.0 cm sin (0.10 πx
cm-1 + 200 πt
s-1).
|
|
|
20.
|
For a string fixed at both ends, the
allowed frequencies are fn = nv/2L, where
n is an integer, v the velocity, and L the length of the string.
For f = 440 s-1 and L = 50 cm, nv =
2fnL = 2(440 s-1)50 cm = 4.4 x 104
cm/s. For a frequency of
528 s-1 = nv/2L’ = 4.4 x 104 cm/s/2L’
or L’ = 2.2 x 104 cm/528 = 41.7 cm.
|
|
|
21.
|
The lowest frequency occurs for n = 1
in fn = nv/2L.
30 s-1 = v/2(60 cm); v = 3.6 x 103
cm/s.
|
|
|
22.
|
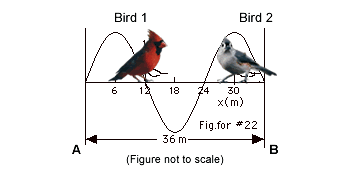
(a) To dislodge bird 2 without disturbing bird 1, she needs
an antinode at the position of bird 2 and a node at the position
of bird 1. With a node at both ends of the wire, the longest
wavelength is in the Fig. for #22 above. From the figure,
3λ/2 = 36 cm, λ
= 24 cm.
(b) f = v/ λ = 48
m/s/24 m = 2 s-1.
(c) For a standing wave, y(x,t) = ym sin
2 πx/ λ
cos 2 πft.
dy/dt = -2π
ym sin 2 πx/ λ
sin 2 πft.
a = d2y/dt2
= -(2πf)2
ym sin 2 πx/ λ
cos 2 πft.
The maximum value of the sine and cosine is 1. If the maximum
absolute value of the acceleration bird 2 can withstand is
48 m/s2, then 48 m/s2 = (2 πf)2ymax,
where ymax is the maximum amplitude he can
withstand.
ymax = 48 m/s2/(4 πs-1)2
= 0.30m. Any amplitude slightly greater than this
is the smallest amplitude needed to dislodge the bird.
|
|
|
23.
|
General equation for a standing wave
is
y(x,t) = ym sin 2πx/ λ
cos 2πft
Compare this with
y(x,t) = 1.0 cm (sin πx/3
cm-1) cos 20 πt
s-1
to find that
(a) A = 1.0 cm,
(b) 2π λ
= π/3 cm-1
or λ =
6 cm, 2 πf = 20 π
s-1 or f = 10 s-1
and v = λf = 6 cm(10 s-1) = 60 cm/s.
(c) We need two waves of the same wavelength and
frequency, traveling in opposite
directions with an amplitude = 0.5 cm.
y1(x,t) = 0.5 cm
sin ( πx/3 cm-1 -
20 πt s-1) and
y2(x,t) =
0.5 cm sin ( πx/3
cm-1 + 20 πt
s-1).
(d) the distance between nodes = λ/2 = 3.0 cm.
(e) v(x,t) = dx/dt = -20 π
cm/s sin πx/3 cm-1
sin 20 πt s-1.
v(1.5 cm, 1/4 s) = -20 π
cm/s (sin π/2) (sin 5 π)
= -20 π(1)(0) = 0.
|
|
|
24.
|
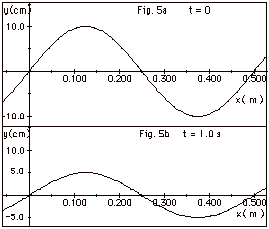
(a) Distance between nodes = λ/2
= 0.250 m. λ = 0.500
m.
(b) For an antinodal point, y(t) = 10.0 cos 2 πt/T.
For t = 1.0 s, 5.0 cm =10.0
cos 2 π s/T.
cos-1 0.50 = π/6
= 2 π s/T.
T = 12 s.
(c) # of half wavelengths in 1.25 m = 1.25 m/0.25 m = 5. There
is a node at both ends. The
rope is fixed at both ends.
(d) Now y(x,t) = A sin 2πx/λ
cos 2 πft = 10 cm sin 4 πx
cm-1 cos πt
s-1/6
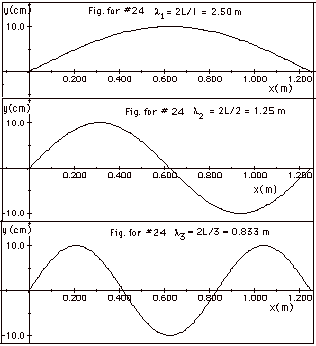
(e) λn =
2L/n. For n = 1, λ1
= 2L = 2(1.25 m) = 2.50 m. For n = 2, λ2
= L =
1.25 m. For n = 3, λ3
= 2.50 m/3 = 0.833 m. The figures are shown below in
Fig. for #24.
|
|
|
25.
|
For a standing wave, y(x,t) = ym
(sin 2 πx/ λ)
(cos 2 πft).
The end at which a string is fixed must have a node, or y
= 0 at that end.
For a string fixed at x = 0, this expression gives
y(0,t) = 0.
For a string also fixed at L, y(L,t) = 0 = ym
(sin 2 πL/ λ)
(cos2 πft).
For this to be 0, sin 2 πL/ λ
= 0 or
2 πL/ λ
= n π and
λn = 2L/n,
where n = 1, 2, 3, . . .
For a string fixed at x = 0, you still use the
sine, but now with the string no longer fixed at L you want
an antinode at x = L, or dy/dx
= 0 at x = L.
dy/dx = 2 πym/ λ
(cos 2 πx/ λ)
cos 2 πft. This
will be zero at all times at x = L if
cos 2πL/ λ
= 0 or
2 πL/ λ
= (n - 1/2) π and
λn = 2L/(n
- 1/2) with n = 1, 2, . .
|
|
|
26.
|
If the observer moves toward the source,
he hears a higher frequency.
f' = f(v + vobs)/v = 85 Hz(340 m/s +
30 m/s)/340 m/s = 92.5 Hz.
|
|
|
27.
|
The siren is at rest with
respect to
- the policeman, and
- the speeder, who travels at the same speed as the cruiser.
So vobs = 0 and they hear a frequency of
2.0 x 103 Hz.
- vsource = 144 km/hr = (144 x 103
m/3600 s) = 40 m/s.
f' = f [ v/(v – vsource)] = 2.0 x 103
Hz[(340 m/s)/(340 - 40)m/s)
= 2.0 x 103 Hz[340/300)] = 2.3 x 103 Hz.
|
|
|
28.
|
Now both the source and
the observer are moving.
Vsource = 30 m/s and vobs
= 20 m/s.
In general, with both in motion, 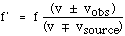
- With the ambulance approaching the car, the source is
moving toward the observer and the observer is moving toward
the source.
f' = f(v + vobs)/(v - vsource) = 400
Hz [(340 + 20) m/s]/[(340 - 30) m/s] = 464 Hz.
- As they recede from each other, the source is moving away
from the observer and the observer is moving away from the
source.
f' = f(v - vobs)/(v + vsource) = 400
Hz [(340 - 20) m/s]/[(340 + 30) m/s] = 346 Hz.
|
|
|