|
|
|
1.
|
A length of #8 copper wire, which has
a radius of 1.63 mm, carries a steady current of 20 A. The
number of electrons per unit volume for copper is 8.47 x 1028
m-3 and its resistively ρ=
1.56 x 10-8 Ω-m.
Find (a) the average current density J, (b) the drift velocity,
and (c) the electric field E. (d) The resistance of
a copper wire with a cross section of 1.2 x 10-6
m2 is 0.012 Ω.
The resistivity of copper is 1.56 x 10-8 Ω - m.
Find the length of the wire.
|
|
|
2.
|
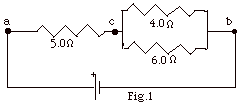
In Fig. 1 below, find Vab
if the current through the 4.0-ohm resistor is 3.0 A.
|
|
|
3.
|
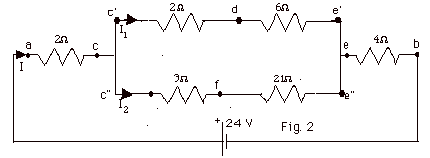
For the circuit of Fig. 2 below, find
the equivalent resistance (a) Rc’e’,
(b) Rc”e”, (c) Rce, (d)
Rab. Find (e) I, (f) Vce,
(g) I1, and (h) I2.
|
|
|
4.
|
Two light bulbs of resistance R1
and R2, respectively, with R1
> R2 are connected (a) in series and (b) in
parallel. Which bulb is brighter in each case? Assume the
resistances of the bulbs remain constant for each wiring.
|
|
|
5.
|
A battery of emf = 30 V and internal
resistance r = 0.5 Ω
is connected in series with two resistances of 9.5 Ω
and 20 Ω (Fig.3
below). Find (a) the current I in the circuit,
(b) the power dissipated in the external and internal resistances
and (c) the power supplied when chemical energy is changed
into electrical energy.
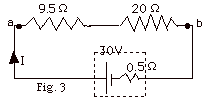
|
|
|
6.
|
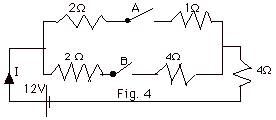
Find the current I in the
circuit of Fig. 4 below when (a) both switches A and B are
closed, (b) only switch A is closed and (c) only switch B
is closed.
|
|
|
7.
|
Two resistors of 10 ohm and 15 ohm in
parallel are in series with a 4.0-ohm resistor. The combination
is in parallel with a 10-ohm resistor. (a) Draw a diagram
for this circuit and (b) find its equivalent resistance.
|
|
|
8.
|
When a resistor with R = 2.0 ohm is connected
to the terminals of a battery, the current through the battery
is 6.0 A. When R is replaced by R’ = 7 ohm, the current
is 3.0 A. Find (a) the emf and (b) the internal resistance
of the battery.
|
|
|
9.
|
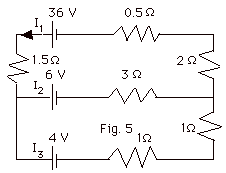
Find (a) I1, (b) I2,
and (c) I3 for the circuit of Fig. 5 below.
|
|
|
10.
|
For an R-C circuit with an initial charge
Qi = 100 µC, resistance R and capacitance
C, the charge decays as a function of a time such that
q(t) = Qi e-t/RC. The time constant
is defined as the time for the capacitor to decay until its
charge q(t) = Qi/e. Find (a) the time constant
for the circuit of Figure 6 below and (b) the time when q
= 50 µC.
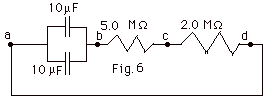
|
|
|
11.
|
A 4.0 µf capacitor is initially
charged to a potential difference of 100 V and then is placed
in series with an open switch S, R, and ε
(Fig.7 below). The + and - signs of C indicate the polarity
of the initial charge. The switch is closed and kept closed
until the steady state is reached. Find the charge on C and
the current in R (a) just as the switch is closed and (b)
when the steady state is reached.
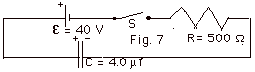
|
|
|
12.
|
A battery with an emf ε
and internal resistance r is connected to a load resistor
R. Find the value of R for which maximum power P is delivered
to the load and sketch P as a function of R.
|
|
|
13.
|
In the circuit of Fig. 8 below, ε
= 6 V and R = 2000 Ω. With
C completely uncharged, switch S is suddenly closed at
t = 0. Determine the current through each resistor for
(a) t = 0 and (b) t = ∞.
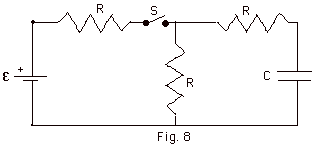
Optional (c) Using Kirchhoff's Rules find expressions for the
currents as a function of time in the three resistors and draw
plots of the currents as a function of time.
|
|