|
|
|
1.
|
(a) Find the magnitude and direction
of the force of +Q on qo at (i) P1 and
(ii) P2 in Fig 1a below. (b) Find the magnitude
and direction of the force of -Q on qo at (i) P1
and (ii) P2 in Fig.1b below. Take Q = 2 x 10-6
C and qo = 10-12 C.
|
|
|
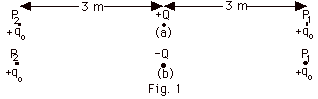
2.
|
Now imagine that all the +qo's
are removed from Fig. 1 above. Find the magnitude and
the direction of the electric field (a) in Fig. 1a and (b)
in Fig. 1b at P1 and P2.
|
|
|
3.
|
(a) Find the electric field at point
P in Fig. 2 below. (b) Repeat for q2 = +1 nC.
|
|
|
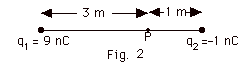
4.
|
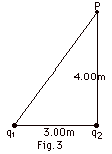
In Fig. 3 below, q1
= +1.00 µC and q2 = -0.0800 µC. Find
the direction and magnitude of the electric field at point
P.
|
|
|
5.
|
Find (a) the electric field, direction
and magnitude, at P (4.00 m, 5.00m) in Fig. 4 below due
to q1 = +5.00 x 10-6 C at (0, 2.00 m),
q2 = -3.00 x 10-6 C at
(4.00 m, 0), and q3 = +1.6 x 10-6 C
at (0, 5.00 m) and (b) the force on q4 =
+2.0 x 10-6 C placed at P.
|
|
|
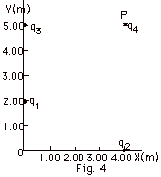
6.
|
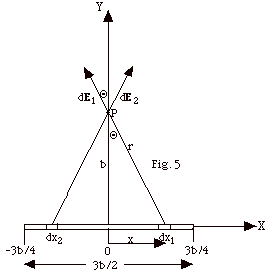
A straight positively charged line coincides
with the X-axis and carries a charge per unit length of λ.
While the charge is actually discrete, it is useful to think
of the charge spread continuously along the line.
Find:
(a) the charge dq on a length dx of the line,
(b) the magnitude of dE1 or dE2
at point P along the Y-axis for the symmetrically displaced
elements of length dx1 and dx2 in Fig.
5 below,
(c) the direction of dE1 + dE2,
and
(d) the magnitude of the component of dE1 or
dE2 in the direction of the resultant field.
Now we can integrate to find the resultant field. Remember that
integration is not a vector addition, so we cannot integrate
until we have found the resultant direction of the field.
(e) In Fig. 5 we have labeled various lengths and an angle:
b, x, r, and Θ. Which of
these is a constant?
(f) Write x in terms of b and a function of Θ.
(g) Find an expression for the resultant dEy in terms
of k, λ, b, a function of
Θ and dΘ.
(h) If you were integrating with respect to x, the lower limit
would be -3b/4 and the upper limit would be +3b/4. What are
the lower and upper limits on the sine of Θ?
(i) Complete the calculation of the resultant electric field
at P in Fig. 5 below.
|
|
|
7.
|
A thin nonconducting wire is bent into
a semicircle of radius R (Fig. 6 below). The wire is
charged so that the linear density λ
= λo cos Θ,
where λo
is a constant. Find the direction and the magnitude
of the electric field at the center of the semicircle at point
O.
|
|
|
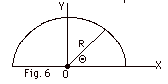
8.
|
A cube with sides of 0.20 m has its center
at the origin of a rectangular coordinate system and its faces
perpendicular to the coordinate axes. The electric field is
E = 100 N/C-m xi. Determine the amount
of charge within the cube.
|
|
|
9.
|
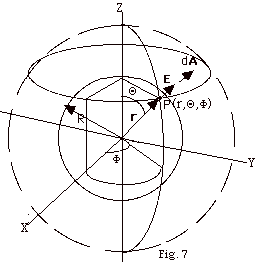
In Fig. 7 below, the dashed spherical
surface is a Gaussian surface of radius r. The solid sphere
is a uniform distribution of charge of radius R. If spherical
symmetry is to be preserved, the electric field E at
P remains constant when the solid sphere is rotated. If this
is true, (a) can the electric field depend on angles Θ
or Φ? (b) must the electric
field E always be radially outward (or inward if the
charge is negative)? and (c) must the electric field be constant
in magnitude everywhere on the Gaussian surface of radius
r? (d) If the angle between the electric field and the surface,
E, dA, is zero how can you write E
. dA? Remember the direction of the
surface is always taken as the outward normal. (e) If E is
a constant, how may you write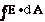 
for the spherical Gaussian surface?
|
|
|
10.
|
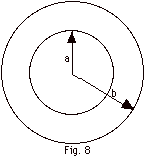
The thick, spherical shell of inner radius
a and outer radius b shown in Fig. 8 below carries a uniform
volume charge density ρwith
total charge Q.
Find:
(a) ρin terms of Q, a,
and b,
(b) the charge enclosed by a spherical Gaussian surface of radius
(i) r < a,
(ii) a < r < b,
and (iii) r > b, and
(c) the electric field for (i) r < a, (ii)
a < r < b, and (iii) r > b.
(d) Use the expressions found in (c) to show that these also
are the electric field for
(i) r ≤ a, (ii) a ≤ r ≤
b, and (iii) r ≥ b.
|
|
|
11.
|
What is (a) the lateral surface area
and (b) the volume of a right circular cylinder of radius
r and length L?
|
|
|
12.
|
Use Gauss's theorem to determine the
electric field due to a very long wire carrying a charge per
unit length + λ a distance
r from the wire.
|
|
|
13.
|
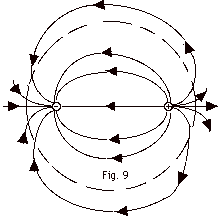
The dashed spherical surface in Fig.
9 is a Gaussian surface, which surrounds a dipole. The solid
curves with arrows represent the field lines for the dipole.
Can Gauss's theorem be used to find the field of a dipole?
Explain your answer.
|
|
|
14.
|
The electric field outside and at a distance
of 0.5 m from the center of a charged sphere, the axis of
a long charged cylinder or an infinite sheet of charge is
144 N/C. For which of these charge distributions do
you find an electric field of (a) 72 N/C, (b) 36 N/C,
(c) 144 N/C at a distance of 1.0 m? Explain your answers.
Find (d) the charge q on the sphere, (e) the charge per unit
length λ on the cylinder
and (f) the charge per unit area σ on
the infinite sheet.
|
|
|
15.
|
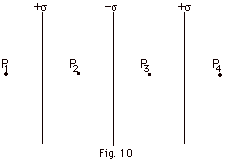
Three infinite sheets of charge are parallel
to each other, as is shown in Fig. 10. The sheet on the left
has a uniform surface charge density +σ,
the one in the middle a uniform surface charge density
- σ, and the
one on the right a uniform surface charge density of +σ.
Find the electric field at (a) P1,
(b) P2, (c) P3, and (d)
P4.
|
|
|
16.
|
A conducting sphere of charge +Q and
radius a is concentric with a very thin conducting spherical
shell of charge - Q and radius b > a. (a)
Where are the charges? Find the electric field for (b)
r ≤ a, (c) a ≤ r ≤ b,
(d) r ≥ b.
|
|
|
17.
|
An infinitely long insulating cylinder
of radius R has a volume charge density that varies with the
radius as ρ = ρo(a
- cr), where ρo,
a, and c are positive constants and r is
the distance from the axis of the cylinder. Find the
electric field at radial distances for (a) r <
R and (b) r > R.
|
|
|
18.
|
Can electric field lines intersect? Why
or why not?
|
|
|
19.
|
A solid sheet of nonconducting material
of thickness t and infinite length and width has a uniform
positive charge density ρ
throughout the sheet. (a) Use Gauss's law to find the electric
field as a function of the distance x from the center of the
sheet for - t/2 < x < t/2. (b) If a
small hole is drilled though the sheet and a particle of mass
m and charge -q is released from rest on one side of the sheet,
what is the frequency of the particle's motion?
|
|
|
20.
|
A uniform electric field E is
set up between two metal plates of length L and spacing d,
as shown in the figure to the right. An electron enters the
region midway between the plates moving horizontally with
speed v. Find an expression for the minimum speed the
electron must have to get through the region without hitting
either plate. Neglect gravitational effects.
|
|
|
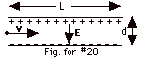
21.
|
An electron is moving in a circular path
around a long, uniformly charged wire carrying 2.5 nC/m. What
is the speed of the electron?
|
|
|
22.
|
A small sphere with mass m carries charge
q. It hangs from a silk thread that makes an angle Θ
with a large, charged nonconducting sheet, as illustrated
in the figure below. Find the sheet's surface charge density
σ.
|
|
|
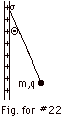
23.
|
Two identical dipoles are placed in a
straight line as shown in Fig. 11a below. Find the direction
of the electric force on each dipole in Fig. 11a. Repeat
for
Fig. 11b below.
|
|
|
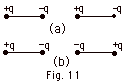
24.
|
An electric dipole consisting of charges
+3.2 x 10-19 C and -3.2 x 10-19 C separated
by 2.0 x 10-9 m is in a field of 5.0 x 105
N/C. Calculate the torque on the dipole when the dipole
moment is (a) parallel and in the same direction as the field
(b) perpendicular to the field and (c) parallel and in the
opposite direction of the field.
|
|
|
25.
|
Two positive point charges repel each
other. Explain this experimental result in terms of the electric
field of one charge action on the other charge.
|
|
|
26.
|
There are really two types of problems
concerning electric fields:
- Given a distribution of charges, find the electric field
due to them.
- Given an electric field E, find the electric force
Fe on a charge q.
Explain two ways of calculating electric fields and how you
find the electric force on a charge q in an electric field.
|
|
|
27.
|
One of two identical nonconducting rods of length L carries
a total positive charge Q and the other carries a total charge
of - Q as shown in Fig. 12 below. (a) Find the electric
field at point P in Fig. 12 due to these charge distributions
as a function of x. (b) What does this expression in
(b) reduce to for x >> L. (c) Identify a dipole
moment for this distribution.
|
|
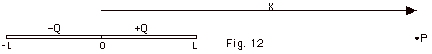
