|
Review - Geometric Optics
|
|
|
1.
|
In Fig. 1 below, label the
angle of incidence Θi,
the angle of reflection Θr,
and the angle of refraction or transmission Θt.
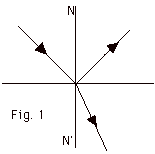
|
|
|
2.
|
As shown in Fig. 2 below, a light ray
hits a surface normally. What is the angle of (a) incidence,
(b) reflection, and (c) refraction?
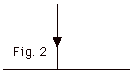
|
|
|
3.
|
For Fig. 3 below, find (a)
the angle of reflection and (b) the angle of refraction. Redraw
Fig. 3 and show the reflected and the refracted rays. The incident
ray is in air with index of refraction ni = 1.00
and transmitted in a medium with index of refraction nt
= 1.50.
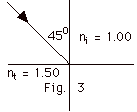
|
|
|
4.
|
Light from a point object
O in Fig. 4 below hits the mirror MM’. Draw one incident
ray from the object that hits the mirror normally and its reflected
ray. Draw another incident ray with an angle of incidence of
about 20o and its reflected ray. Since we think of
light as coming from rays diverging from an object, it appears
that the reflected light comes from a point behind the mirror.
Dash the reflected rays behind the mirror until they meet and
label this point I for image. Compare the distances of O and
I from the mirror.

|
|
|
5.
|
A light beam is incident upon a parallel
glass plate, as shown in Fig. 5 below. Find the angle of (a)
refraction at the first glass surface, (b) incidence at the
lower glass-air surface, (c) refraction as the ray goes from
glass to air. Use these angles to trace the path of the ray
from air to glass and then from glass to air.
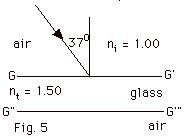
|
|
|
6.
|
A beam of light of wavelength λ is
incident from air upon the prism (n = 1.532) of Fig. 6 below
at an angle of 50o. Find the angle of (a) refraction
as the light enters the prism, (b) the angle of incidence at
the other side of the prism, and (c) the angle of as the ray
passes from glass to air. Use these angles to trace the path
of the ray from air to glass and then from glass to air. (d)
If light of wavelength λ’
> λ for which its index
of refraction n’ is less than n, compare its path into
and through the prism with that of the path for the light of
wavelength λ.
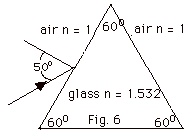
|
|
|
7.
|
Light is incident from a medium ni
at an angle of 48.6o as shown in Fig. 7 below.
What is (a) the angle of refraction in air and (b) the index
of refraction ni of the medium? (c) The angle of
incidence is now increased to 60o. Using Snell's
law and the ni you found in part (b), find the sine
of the new angle of refraction. This is impossible. What happens?
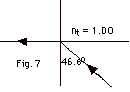
|
|
|
8.
|
As shown in Fig. 8 below, a light ray
is incident normally on one face of
a 30o-60o-90o dense flint
(n = 1.655) prism that is immersed in water
(n = 1.333). (a) Determine the exit angle Θ4
of the ray. (b) A substance is dissolved in the water to increase
the index of refraction. At what value of n of the mixture will
total internal reflection cease at point P?
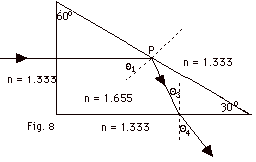
|
|
|
9.
|
A cylindrical tank with an open top has
a diameter of 3.0 m and is completely filled with water. When
the setting sun reaches an angle of 28o above the
horizon, sunlight ceases to illuminate the bottom of the tank.
How deep is the tank?
|
|
|
10.
|
A microscope is focused on a small scratch
on the top surface of a glass slide. When a cover slip with
a thickness of 500 µm is placed on the slide, the microscope
must be raised by 120 µm to bring the scratch back into
focus. What is the index of refraction of the cover slip? Assume
that all rays entering the microscope make small angles with
the normal to the slide so that sin Θ is
approximately equal to tan Θ.
|
|
|
11.
|
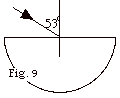
A light ray is incident upon a semicircular
container of water at an angle of 53o as shown in
Fig.9 below. The index of refraction of water is 4/3. Trace
the path of the ray through the water and out into the air,
labeling angles of incidence and refraction. Ignore any refraction
at the surface of the container.
|
|
|
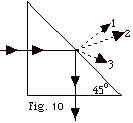
12.
|
A ray of light is incident normally on
one face of a triangular prism of glass as shown in Fig. 10
below. The light is totally internally reflected inside the
prism. (a) What is the minimum index of refraction of the prism
that will cause all the light entering the prism to emerge as
shown? (b) If the index of refraction is too small, some light
will be refracted at the diagonal face. Which path (1, 2, or
3 of Fig. 10) will it follow? Explain your answer.
|
|
|
13.
|
A thin converging lens has a focal length
of 10 cm. Find by (i) calculation and (ii) construction
of a ray diagram the position of the image of an object for
the object distance so equal to (a) 30 cm, (b) 15
cm, and (c) 5.0 cm. Also find the magnification for each case.
Describe whether the image is real or imaginary, erect or inverted,
magnified or diminished.
|
|
|
14.
|
A thin diverging lens has a focal length
of 10 cm. Find by (i) calculation and (ii) construction
of a ray diagram the position of the image of an object for
object distance equal to (a) 30 cm and (b) 4 cm. Also find the
magnification for each case. Describe whether the image is real
or imaginary, erect or inverted, magnified or diminished in
size.
|
|
|
15.
|
An object 1.0 cm high is 100 cm from
a converging lens. The inverted image is 3.0 cm high. Find the
focal length of the lens.
|
|
|
16.
|
When a person holds a magnifying glass
8.0 cm away from an object that is 2.0 cm wide, she sees
a virtual image of the object, which is 6.0 cm wide. What is
the focal length of the magnifying glass?
|
|
|
17.
|
A projector forms an image of a 5.0 cm
x 5.0 cm slide on a screen. If the image is 95.0 cm on a side
and the distance from the slide to the screen is 4.00 m, what
is the focal length of the projector's lens?
|
|
|
18.
|
When an object is placed 12 cm to the
left of a lens, a virtual image is formed 6.0 cm from the lens
on the same side as the object. What is the focal length of
the lens? Is it a converging or a diverging lens?
|
|
|
19.
|
The objective and the eyepiece of a microscope
each have a focal length of 2.0 cm. If an object is placed
2.2 cm from the objective, calculate (a) the distance between
the lenses when the microscope is adjusted for minimum eyestrain
and (b) the magnification of the microscope.
|
|
|
20.
|
A comet-seeker's telescope has an objective
lens of focal length 40 cm and an eyepiece of power 30 diopters.
What is the magnifying power of the microscope?
|
|
|
21.
|
Find by calculation and construction
of ray diagrams the image of a concave mirror of focal length
10 cm when so is (a) 30 cm and (b) 5 cm. Find the
magnification and classification of the image for both cases.
|
|
|
22.
|
Rays parallel to the principal axis of
a converging lens and concave mirror pass through the lens and
are reflected by the mirror, which is to the right of the lens.
If the distance between the lens and mirror is (f1 +
f2), where f1 and f2 are the
focal lengths of the lens and mirror, respectively, locate the
final image. The incident light is incident from the left of
the lens.
|
|
|
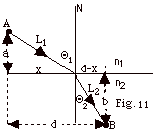
23.
|
Fermat's principle states that a light
ray that connects two points within a medium follows a path
for which the transit time of the light is a minimum. The length
traveled by the light L = ct for vacuum or air and L = vt =
ct/n or t = nL/c for a medium of index refraction n. If light
travels the shortest distance, it takes the minimum time.
Use Fermat's principle to prove Snell's Law: n1 sin
Θ1 = n2
sin Θ2.
Refer to Fig. 11 below and find when dt/dx = d(n1L1/c
+ n2L2/c) = 0.
|
|
|
24.
|
Two converging lenses, both of focal
length 10 cm, are separated by 20 cm. An object is 15 cm to
the left of the first lens. Find by calculation and construction
of a ray diagram the position of the image. Find the magnification
of the image and describe whether it is real or imaginary, erect
or inverted, magnified or diminished.
|
|
|
25.
|
A double convex lens with equal curvature
radii of 38-cm is made from glass with indices of refraction
of 1.51 for red light and 1.54 for blue light. If a point source
of white light is place on the lens axis at 95 cm from the lens,
over what range will its visible image be smeared?
|
|
|
26.
|
A person has a far point at 4.0 m. Describe the lens that
will correct this defect.
|
|
|
27.
|
A person has a near point
at 1.25 m. Describe the lens that will correct this defect.
|
|