Review - Induction

1.

A square loop of wire, 2.0 m on a side, has a resistance of 0.04 ω. The loop is in a horizontal plane. Initially a magnetic field B = 0.080 T points vertically downward. If this magnetic field is reduced in magnitude at a constant rate to 0.040 T in 2.0 s, find the current and the sense of the current as you look down on the loop. Note: 1 T = 1 N/A-m.

2.

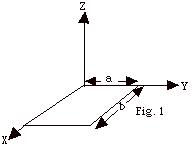
A rectangular single-turn loop, with dimensions a = 0.10 m and b = 0.15 m, lies in the X-Y plane, as shown in Fig. 1. Within the loop there is a time-dependent magnetic field B = 0.0120 N/A-m²(x sin10³ s^-1tj + y cos 10³ s^-1tk). Determine the emf induced in the loop due to the changing magnetic field.

3.

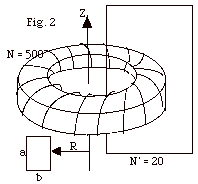
A toroid with a rectangular cross-section (a = 0.02 m and b = 0.03 m) consists of N = 500 turns of wire that carries a current I = I_o sin ωt.  A loop that has N’ = 20 turns of wire links the toroid (Fig. 2).  I_o = 50 A and ω = 120 π s^-1. Determine the emf induced in the loop by the changing current I.

4.

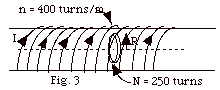
A long solenoid has n = 400 turns/m and carries a current I = 30 A(1 - e^-1.6t/s). Inside the solenoid and coaxial with it is a loop that has a radius R = 0.06 m and consists of N = 250 turns of wire (Fig. 3). What is the emf induced in the loop?

5.

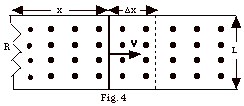
Figure 4 below shows a conducting rod of length L being pulled along horizontal, frictionless, conducting rails at a constant velocity v. A uniform vertical magnetic field B out of the page fills the region in which the rod moves. Find (a) the magnetic flux when the rod is a distance x from the left end of the conducting rails, (b) the change in magnetic flux when the rod moves to the right a distance Δx, (c) the induced emf ε, (d) the direction of the induced current, (e) the induced current in the loop of total resistance R, (f) the power dissipated in the resistance R in terms of B, L, v, and R, (g) the force that must be applied by an external agent to maintain the motion, (h) the power supplied by the external agent, and (i) a comparison of the answers to (f) and (h).

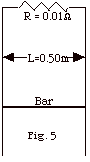
6.

A bar of mass m = 0.50 kg slides downward along stationary wires that are separated by a distance L = 0.5 m and are joined at the top by a resistance R = 0.010 ω (Fig. 5 below). A uniform magnetic field B = 0.20 N/A-m points into the paper. (a) If the bar slides down, what is the sense of the current through it? (b) At what speed v will the bar experience no force?

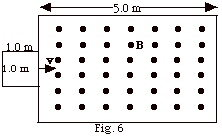
7.

A square loop of wire 1 m on a side moves with a speed v = 0.5 m/s into a region of a magnetic field B = 1.0 T out of the page, as shown in Fig. 6 below. At t = 0, the loop of wire is just about to enter the magnetic field. (a) Plot the magnetic flux through the loop of wire as a function of time at 1-s intervals for 12 s. (b) Now plot the induced emf in the coil for the same time and interval of time. (c) If the coil has a resistance R = 0.01 ω,  find the induced current in the coil at the various times. Describe the sense of the current as the coil passes through and out of the field.

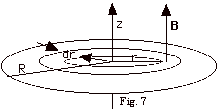
8.

The axis of a circular loop of radius R coincides with the z-axis (Fig. 7). At all points within the area of the loop there is a non-uniform and time-varying magnetic field B normal to the plane of the loop and directed along the +z-axis. The magnitude of the field at any point r distant from the axis is given by
B = B_o N/A-m - C N/A-m³-s² r²t², where B_o and C are positive constants. Find (a) the instantaneous magnetic flux dΦ through the ring-like area of radius r and thickness dr, (b) the instantaneous flux Φ which links with the area of the loop of radius R, (c) the emf induced in the loop and (d) the direction of positive charge circulation when the loop is observed from above.

9.

A rod with length L, mass m and resistance R slides without friction down two parallel conducting rails inclined at an angle Θ with the horizontal. The rails and the bar that connects them at the bottom of the incline have negligible resistance. Find the constant velocity v achieved by the wire in a uniform magnetic field B directed vertically upward.

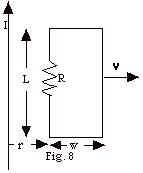
10.

A rectangular loop of length L and width w moves with velocity v away from a long wire that carries a current I in the plane of the loop (Fig. 8). The total resistance of the loop is R. Derive an expression that gives the current in the loop at the instant the near side is a distance r from the wire. Is the induced current clockwise or counterclockwise in the loop?

11.

A long solenoid has n turns per unit length and a radius R. (a) What is its inductance per unit length? (b) If the solenoid has 2000 turns per meter and a radius of 0.02 m, find the inductance for a 1.0 m segment of this solenoid. (c) If the current in the solenoid is changing at the rate of 3.0 x 10² A/s, find the induced emf in this segment.

12.

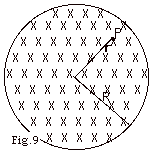
A magnetic field directed into the page changes with time according to B = (0.05s^-2t² + 0.4)T. The field has a circular cross-section of radius R = 0.05 m (Fig. 9). What are the direction and the magnitude of the electric field E at point P when t = 4 s and r = 0.04 m?

13.

To measure the inductance and the internal resistance of an inductor, a physicist first connects the inductor across a 3.0 V battery. She measures a final, steady current of 24 A. Then she short-circuits the inductor with a resistanceless wire and finds that the current decreases from 24 A to 12 A in 0.22s. Find (a) the internal resistance and (b) the inductance of the inductor.

14.

An LC circuit has an inductance of 5.0 x 10^-2 H and a capacitance of 5.0 x 10^-6 F. At t = 0, the capacitor is fully charged with q_m = 1.0 x 10^-4 C.  (a) What is the energy in this circuit? (b) At what time, after t = 0, will the energy be purely magnetic? (c) At what later time will it be purely electric again?

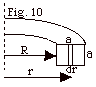
15.

A toroid of square cross section has inner radius R and sides a as shown in Fig. 10. The toroid has N turns and carries a current I.  Find (a) the inductance of the toroid, (b) the magnetic energy density of the toroid, (c) the total magnetic energy stored in the toroid. (d) Use the expression for the magnetic energy U = 1/2 LI² and compare with your answer to (c).

16.

Complete the relations below in terms of the field quantities E and/or B and give the meaning of the term appearing on the right side:

(a) d /dt ∫ B ^. dA =
where the left-hand side represents the time rate of change of the magnetic flux.

(b) µ_oε_o  d /dt ∫ E ^. dA
where the left-hand side represents the time rate of change of the electric flux.

17.

Consider the case of linearly polarized plane electromagnetic waves in free space where the phase velocity of the waves is c = 3 x 10⁸ m/s.

Prove the following:

(a) The Poynting vector may be expressed as ε_oc²E x B.

(b) The electric and magnetic field energy densities are equal.

(c) S_av = (1.33 x 10^-3 C²/N-m-s)E²_m, where E_m is the maximum value of E.

18.

Consider a long cylindrical conductor of radius r and length L.  A steady current I is distributed uniformly across the cross section of the conductor whose resistance is R. Calculate (a) the magnitudes of the electric and magnetic fields at the surface of the conductor, (b) the magnitude of the Poynting vector, and (c) show that energy flows into the conductor across its surface at a rate which is equal to the rate of heat production within the conductor.

19.

A laser produces an average power or 7.0 W in a light beam 1.00 mm in diameter. Find (a) the average intensity and (b) the maximum value of the electric field.

20.

A parallel plate capacitor consists of two circular plates of radius R and separation d. The charge q on the plates varies with time such that q =
q₀ sin ωt. Find an expression (a) for the electric field E between the plates in terms of q, (b) for the electric flux Φ_E for a distance r ≤ R from the axis of the plates, (c) for the magnetic field B at this distance r and (d) for the Poynting vector S. (e) Show that when the capacitor is being charged, S is directed toward the axis of the plates and that there is a flow of energy into the region between the plates. (f) Calculate the rate of energy flow into the capacitor through the gap between the plates and compare the result with the rate of increase of field energy in the volume between the plates.

21.

An LRC series circuit has  L = 10 mH,  C = 1.0 µF,  R = 3.3 ω  across a potential difference of 1.0 V.  Find (a) the resonance frequency ω_o, (b) the maximum current I_p in the circuit at resonance, (c) the average power dissipated per period at resonance, (d) the maximum current I_p in the circuit and the average power dissipated per period when the frequency is 5 percent lower than the resonance frequency.

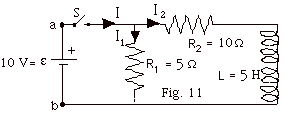
22.

In the circuit of Fig. 11, ε = 10 V, R₁ = 5.0 ω,  R₂ = 10.0 ω, and L = 5.0 H. For the switch S just closed, find the values of (a) the current I₁ through R₁, (b) the current I₂ through R₂, (c) the current I through the switch, (d) the potential difference across R₂, (e) the potential difference across L, and (f) dI₂/dt. Repeat all of the above for a time when the switch has been closed for a very long time.

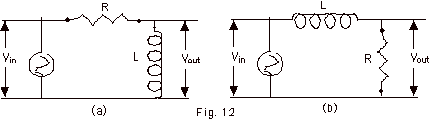
23.

(a) For the circuit of Fig. 12a, write an expression for the ratio of V_{p out} to V_p in. Sketch a graph of V_{p out} / V_{p in} as a function of ω. (b) Repeat (a) for Fig. 12b. For which of the two circuits is there a preferential for the high frequencies (called a high-pass filter)? The other one is called a low-pass filter because there is a preferential for the low frequencies.

24.

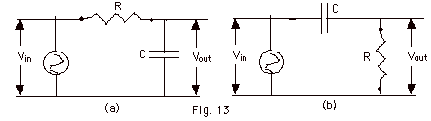
(a) For the circuit of Fig. 13a, write an expression for the ratio of V_p out to V_p in. Sketch a graph of V_{p out} / V_{p in} as a function of ω. (b) Repeat (a) for Fig. 13b. For which of the two circuits is there a preferential for the high frequencies (called a high-pass filter)? The other one is called a low-pass filter because there is a preferential for the low frequencies.

25.

The average power P_av = I_rms² R.  (a) Show that this can also be written as V_rms² Rω²/[R²ω² + L²(ω² - ω_o²)², where ω_o = (1/LC)^1/2. (b) Find the maximum value of the average power when ω = ω_o. (c) Sketch a graph of P_av as a function of ω. (d) Find the values of the ω's for which the average power is one-half the maximum value. (e) The sharpness (narrowness of the maximum) of a graph of P_av as a function of ω is usually called the quality factor. The quality factor is denoted by Q_o (note it has nothing to do with charge) and is given by Q_o = ω_o/Δω, where Δω is the difference between the two values of ω you found in (d). Using your result found in (d) show that you may write Q_o = ω_oL/R.

26.

Can the amplitude of the voltage across an inductor be greater than the amplitude of the generator voltage in an RLC circuit? Consider an RLC circuit with V_p = 10 V,  R = 10 ω,  L = 1.0 H, and C = 1.0 µF.  Find the amplitude across the inductor at resonance.