|
|
|
1.
|
Given that the magnetic force Fm on a
positively charged particle with charge q traveling with a
velocity v in a magnetic field B is Fm
= q(v x B), where the unit of B is Tesla
(T), find the Tesla in terms of the following units: N, C,
m, and s or N, A, and m.
|
|
|
2.
|
The magnetic force Fm
on a charge q moving with a velocity v in a magnetic
field B is given by Fm = q(v
x B). Which of the following statements are always
true? (a) Fm is always perpendicular to
v. (b) v is always perpendicular to B.
(c) Fm is always perpendicular to B.
|
|
|
3.
|
A uniform magnetic field B, with
magnitude B = 1.2 x 10-3 T, points vertically upward
throughout the volume of a laboratory chamber. A proton with
a velocity v = 3.2 x 107 m/s enters the laboratory
moving horizontally from south to north. Find (a) the magnitude
and (b) the direction of magnetic force on the proton.
|
|
|
4.
|
A proton moves in a uniform magnetic
field B with a speed of 107 m/s and experiences
an acceleration of 2 x 1013 m/s2 in
the +X-direction when its velocity is in the +Z-direction.
Determine the magnitude and direction of the magnetic field
for which the magnitude of the field is a minimum.
|
|
|
5.
|
An electron moves with a speed v = 2
x 107 m/s through a magnetic field of B = 0.080
N-s/C-m. (a) What are the greatest and smallest forces the
magnetic field may exert on the electron? (b) If the acceleration
of the electron is
1.41 x 1017 m/s2, what angle does
the velocity make with the magnetic field? The electron has
a mass m = 9.1 x 10-31 kg and its charge e = 1.6
x 10-19 C.
|
|
|
6.
|
A particle of charge q = 10-6 C
moves to the right with velocity v = 103 m/s in
a magnetic field B = 2 N-s/C-m which makes an angle of 30o
with v. Find the magnitude of the force on the charged
particle.
|
|
|
7.
|
An electron moving with velocity v
enters a constant magnetic field. What will its path through
the field look like if it enters (a) parallel to the field
direction? (b) perpendicular to the field direction?
(c) at some other angle to the field direction? (d) In which
of the above cases will the electron be accelerated?
|
|
|
8.
|
Two charged particles with the same mass
and charge q move in circular paths in a magnetic field B
that is perpendicular to their velocities. If particle A has
a velocity vA and particle B has a velocity vB,
compare the time for the particles to make one complete orbit.
|
|
|
9.
|
Single ionized neon atoms (neon atoms
that have lost one electron) enter a uniform magnetic field
B. All of the atoms have the same velocity v,
which is perpendicular to B. The radius of the circular
path of the atoms with mass m1 is 20 cm and for
those with mass m2 it is 22 cm. What is the ratio
of m2 to m1?
|
|
|
10.
|
In a space laboratory, an object of mass
m = 10-3 kg and charge q = 2 x 10-5
C moves in a circular orbit of radius r = 102 m
about a fixed charge Q = -10-4 C. There is a uniform
magnetic field B = 4 N-s/C-m down into the plane of the orbit.
Find (a) the magnitude and direction of the electric force
acting on the object of mass m, (b) the magnetic force on
the object in terms of its velocity v, (c) the direction of
the magnetic force if (i) the object moves in a clockwise
direction as you look down at the orbit and (ii) if the object
moves in the opposite direction. (d) Use Newton's second law
of motion to determine for what velocity v the object will
move in a circle of radius 102 m. Your solution
will lead you to a quadratic equation. Your knowledge of physics
will allow you to interpret the solutions.
|
|
|
11.
|
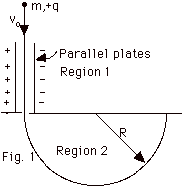
A particle with a mass m = 2.0 x 10-12
kg velocity v = 106 m/s and charge
q = 10-6 C enters region 1 between
the parallel plates where there is an electric field E = 106
N/C. Find (a) the direction and magnitude of the magnetic
field B perpendicular to the velocity of the particle in Region
1 that allows the particle to pass through Region 1 without
a deflection, (b) the direction of the deflection of the particle
with B as found in (a) if its velocity is (i) 5 x 105 m/s
and (ii) 5 x 106 m/s. The particle now enters Region
2 where there is no electric field, but a magnetic field B’
= 2.0 T perpendicular to v. The magnitude of v is again
106 m/s. (c) What is the direction of B’
to make the particle go in a counterclockwise circular path?
(d) What is the radius of the circle?
|
|
|
12.
|
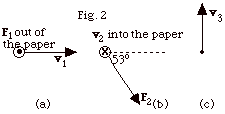
In a certain region of space there is
a magnetic field B, but no electric field. A particle of charge
+10-6 C, moving to the right at v1
= 500 m/s, experiences a force F1,
directed out of the paper, of magnitude 3.0 x 10-3 N
(Fig. 2a below). The same particle moving into the paper at
v2 = 500 m/s experiences a force F2
in the plane of the paper (Fig. 2b below). Find (a) the magnitude
and direction of B. (b) the magnitude of F2
and (c) the magnitude and direction of F3
on the particle if it moves with velocity v3
= 103 m/s as shown in Fig. 2c below. (d) If the
particle has mass m = 10-8 kg, where is the center
of the circular orbit for the velocity in Fig. 2b? For this
figure describe the plane in which it moves.
|
|
|
13.
|
Two smooth conducting rails a distance
L = 2.0 m apart make an angle of 22.5o
with the horizontal. A bar of mass 1.2-kg rests across
the rails, as shown in Fig. 3 below. There is a uniform
magnetic field vertically upward equal to
0.50 N-s/C-m. A battery is connected to cause a current I
to flow through the bar as shown. (a) Draw a side view of
the bar and indicate the cause and direction of each force
that acts on it. There is no friction, but do not forget gravity.
(b) What current I will allow the bar to remain at rest?

|
|
|
14.
|
A wire carrying a current is in a north-south
direction. The north-seeking pole of a compass needle placed
above the wire is deflected toward the west. What is the direction
of the current in the wire?
|
|
|
15.
|
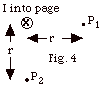
Figure 4 below represents a wire carrying
a current into the page. Sketch a magnetic field line due
to the current-carrying wire. What is the direction of the
magnetic field at P1? at P2?
|
|
|
16.
|
The magnetic field B due to a very long
wire carrying a current I at a distance r from the wire is
0.50 T. Find the magnetic field due to the long wire
if (a) I is doubled and r is halved or (b) I is halved and
r is doubled.
|
|
|
17.
|
Figure 5 below represents two wires carrying
currents into the page. (a) What is the magnitude of the magnetic
field at point P1, which is halfway between the
wires, if both wires carry current I. (b) What is the direction
and magnitude of the magnetic field at P2. (c)
If a proton moves out of the paper at P2 parallel
to the current-carrying wires, what is the direction of the
force exerted on it?

|
|
|
18.
|
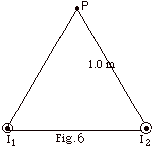
Two very long wires carrying a current
I of 3.0 A out of the page are at two of the corners of an
equilateral triangle, as shown in Fig. 6 below. The sides
of the triangle are 1.0 m long. Find the direction and magnitude
of the magnetic field at P, the third corner of the triangle.
|
|
|
19.
|
Two parallel wires carrying current in
the same direction attract each other. Describe this experimental
result as an interaction between the field due to one wire
and the motion of charges in the other wire.
|
|
|
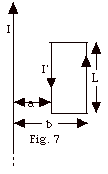
20.
|
In Fig. 7 below, the very long straight
wire carries a current I = 10 A and the rectangular loop carries
a current I’= 20 A. Find the magnitude and direction
of the force on the loop. a = 0.01 m, b = 0.03
m, and L = 0.03 m.
|
|
|
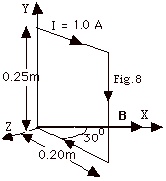
21.
|
The rectangular loop of Fig. 8 has a
length of 0.25 m and width of 0.20 m. It is hinged along the
y-axis and rotates about this axis. The plane of the coil
makes an angle of 30o with the X-axis. The coil
carries a current I = 1.0 A and is in a magnetic field B
= 0.5 N/A-m. Find the torque on the loop.
|
|
|
22.
|
If the current in a circular loop is
in a counterclockwise direction as you view it, what is the
direction of the magnetic field due to the current carrying
loop along its axis?
|
|
|
23.
|
An electron travels with a velocity v
along the axis of a current-carrying loop. What will happen
to the electron?
|
|
|
24.
|
A long solenoid with 1000 turns per meter
carries a current of 0.20 A. As viewed from the right
end of the solenoid, the current in the coils of the solenoid
is counterclockwise. (a) Find the direction and magnitude
of the magnetic field due to the solenoid. A current of 6.0
A exists in a long straight wire along the axis of the solenoid,
with the direction of the current to the left. (b) Find at
what radial distance the direction of the resultant magnetic
field due to the solenoid and the long straight wire is at
an angle of 45o to the axial direction of the solenoid.
|
|
|
25.
|
I describe a toroid as a solenoid bent
into the shape of a doughnut. For a toroid with inner radius
a and outer radius b, find the magnetic field of the toroid,
which carries a current I, for (a) r ≤ a,
(b) a ≤ r ≤ b, and (c) r ≥ b.
|
|
|
26.
|
In the review for electric fields, I
commented that there were two problems related to electric
fields: (a) given a distribution of charges, find the electric
field due to them and (b) given an electric field, find the
force on a charge particle q in this field. Please do
a similar analysis for magnetic fields.
|
|
|
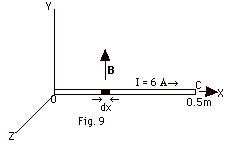
27.
|
A thin, straight, rigid wire coincides
with the X-axis with the left end at the origin 0 and the
other end at C. A steady current of 6.0 A is directed from
0 to C. The other end of the wire is at x = 0.5 m. Over the
entire length OC, there is a magnetic field B directed
along the Y-axis. The magnitude of the field B = (1 T + 3x2 T/m2).
Find (a) the magnitude of the force dF exerted on the
current element I dx, (b) the units and direction of dF,
(c) the magnitude of the torque dτ
exerted on the element dx about the Y-axis, (d) the magnitude
of the torque dτ exerted
on the element dx about the Z-axis and (e) the force on the
entire length OC due to the magnetic field B.
|
|
|
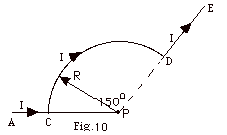
28.
|
A steady current I is maintained in the
conducting path ACDE of Fig. 10 below. Find the magnetic field
at P located at the center of the circular arc CD of radius
R subtending an angle of 150o. What is the
direction of B?
|
|
|
29.
|
Bending a very long wire as shown in
Fig. 11 forms a long hairpin. If the wire carries a current
I, what is the magnitude and direction of the magnetic field
at point P. Your answer will be in term of symbols. The radius
of the loop at the left end is very small compared to the
lengths of the straight sections of the wire.

|
|
|
30.
|
In the coaxial arrangement of Fig. 12
below, a current I in the inner cylinder of radius a is out
of the page and a current I in the outer cylindrical shell
of inner radius b and outer radius c is into the page. Find
the magnetic field (direction and magnitude) for (a) r ≤
a, (b) a ≤ r ≤ b, (c) b ≤ r ≤ c, and
(d) r ≥ c.
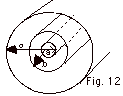
|
|
|
31.
|
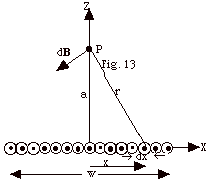
Figure 13 below shows a cross-sectional
view of a large number N of long, thin, straight wires which
are closely spaced in the X-Y plane, forming a single layer
w in width. Each wire is parallel to the Y-axis and carries
a current I out of the X-Y plane (i.e., the plane of the paper).
(a) Starting with the expression B = µoI/2 πr
that represents the magnetic field due to an infinitely long,
slender wire, write an expression for dB, the contribution
to the magnetic field at P due to the current in an element
of width dx located at a distance x from the origin. The point
P is located on the Z-axis a distance a from the X-Y plane
and is equidistant from the edges of the layer.
(b) Calculate B due to the current in the entire layer of
width w.
|
|
|
32.
|
You found that the magnetic field B of
a circular loop of radius R carrying a current I at a point
P on the axis of the loop a distance z from the center of
the loop is given by B = µoI πR2/2 π(R2
+ z2)3/2. (a) What does the magnetic
moment µ of the loop equal? (b) Rewrite B in terms
of the magnetic moment µ of the loop. (c) Find the expression
for B from Part (b) when z is much greater than R. (d)
Find the magnetic field due to a spinning electron with magnetic
moment µ = 9.27 x 10-24 A-m2 at
P a distance z = 10-10 m. A second spinning
electron is at P on the axis of spin of the first one. (e)
Find the potential energy (in electron volts) of the magnetic
moment of the second electron in the magnetic field of the
first spinning electron if the two electron spins are (i) parallel
and (ii) antiparallel. Which orientation has the
least energy?
|
|