|
|
1.
|
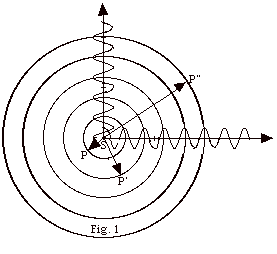
The circles in Fig. 1 below represent
cross-sections of spherical wave fronts emanating from a source
S. All points on a wave front are in phase. (a) What do the
concentric circles pass through for each of the sinusoidal
waves shown in Fig. 1? Find the distances (b) SP, (c) SP’,
and (d) SP” in terms of wavelength λ.
(e) If you wished to draw wave fronts through troughs in Fig.
1, where and how would you draw them?
|
|
|
2.
|
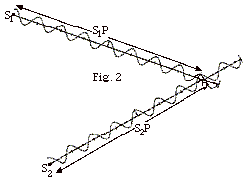
In Fig. 2 below, two sources S1
and S2 emit waves. The two waves overlap
at P. Find (a) the length of the path from S1
to P, S1P, (b) the length of the path from
S2 to P, S2P, and (c) the path difference
(S1P - S2P) in terms of the wavelength
λ. (d) Will the
disturbances of the two waves at P produce constructive or
destructive interference? Explain your answer.
|
|
|
3.
|
Write a mathematical equation that shows
the relation among the quantities: frequency, wavelength,
and velocity of a wave?
|
|
|
4.
|
A person is at equal distances from two
speakers of a stereo hi-fi system and hears a note of single
frequency equal to 275 Hz (275 s-1). He moves sideways
until he hears the note fade to a minimum. At this position
he is 10 feet from the left speaker and 8 feet from the right
speaker. Find the speed of sound.
|
|
|
5.
|
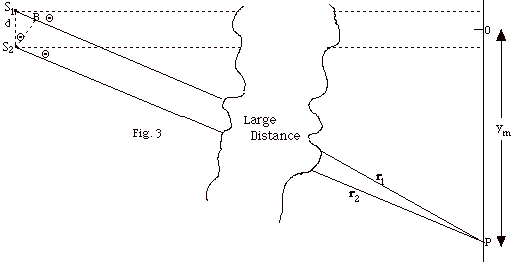
Figure 3 below shows two point sources,
S1 and S2 emitting waves that are detected
at a distant point P from the two sources. When the distances
r1 and r2 from sources 1 and
2 to the point P are large compared with the separation d
of the sources, the two rays along the lines of sight from
the two sources to point P are nearly parallel, both being
essentially at the same angle Θ
from the X axis as shown in the figure. Since I am unable
to draw such large distances and at the same time show the
path difference, S1P - S2P = S1P,
as a reasonable length, I have made a "break" in
the drawing as the two "parallel" rays come together
and arrive at P.
(a) If point P is one of maximum intensity (constructive interference), find
S1P in terms of the wavelength λ.
(b) Use triangle BS1S2 to find
an expression in terms of the separation d of the sources
and a function of Θ that
you can equate to the path difference found in (a).
(c) Repeat (b) for the case in which P is a point of
minimum intensity
(destructive interference).
|
|
|
*6.
|
Let us take the frequency f of the two
sources in Fig. 3 above to be the same and say the waves travel
in the same medium so the wave produced by S1 has
the same wavelength λ
as the wave produced by S2. The equation of the
wave produced by S1 is y1(r1,t)
= A1 sin (2 πvt
- 2 πr1/ λ)
and the equation of the wave produced by S2 is
y2(r2,t) = A2 sin (2pnt
- 2 πr2/ λ).
At P in Fig. 3, the phase difference between the two
waves is ΔΦ = (2 π/ λ)(r1
- r2), where r1 is greater than
r2.
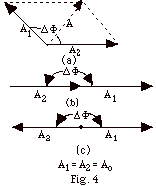
In Fig. 4 below we take the amplitudes of the waves A1
= A2 = Ao and draw "phasor diagrams."
While amplitudes are not vectors, you can use the phasors
to find the resultant amplitude.
In Fig. 4b, (a) find the resultant amplitude in terms of Ao,
and (b) the values of ΔΦ
in radians that would produce this amplitude.
In Fig. 4c, (c) find the resultant amplitude in terms of Ao,
and (d) the values of ΔΦ in
radians that would produce this amplitude.
|
|
|
*7.
|
You probably found that the resultant
amplitude in Fig. 4b was 2Ao and
ΔΦ = 2m π
where m = 0, 1, 2, 3, 4, . .
(a) Since it is always true that ΔΦ
= (2 π/ λ)(r1
- r2), use your result to find the path difference
(r1 - r2).
(b) Now use your results of Problem 6 part d to find the path
difference when point P in Fig. 3 above is one of destructive
interference.
|
|
|
8.
|
In figure 5 above, you found
the path difference (r1 - r2) = d sin
Θ = m λ,
where m = 0, 1, 2, 3, . . . . for constructive
interference.
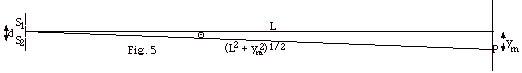
(a) In Fig. 5 below, point P is
a point on the screen for the mth maximum. The distance
from the center of the screen to P is ym.
L is the distance of the slits to the screen. For cases
in which ym is much smaller than L, find
ym in terms of m, λ,
and d.
|
(b) Find the distances between maxima
or Δy = ym+1
- ym.
|
| (c) Repeat (a) and (b) when point
P is a point on the screen for the mth minimum. |
|
|
|
*9.
|
(a) Use Fig. 4a above to show that in
general the square of the resultant amplitude A2
= 4Ao2 cos2 ΔΦ/2.
Hint: Find the components of A1 along the
X and Y-axes and then the X and Y components of the resultant
A of A1 and A2. Use the trigonometric
identity cos2 ΔΦ/2
= 1/2 + 1/2 cos ΔΦ.
(b) The intensity I is proportional to the square of the amplitude.
The resultant intensity I = 4Io cos2
ΔΦ/2, where Io
is the intensity due to one source and ΔΦ/2
= πd sin Θ/ λ.
Sketch I as a function of d sin Θ.
|
|
|
*10.
|
Three radio antennas arranged as shown
in Fig. 6, emit waves of wavelength λ =180
m, all in phase, with the same amplitude Ao and
intensity Io. Find the intensity of the resultant
waves from the three antennas at a point far from the antennas
for the directions (a), (b), and (c) shown in Fig. 6 below.
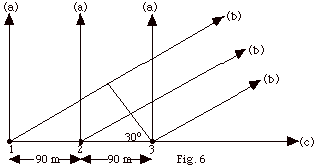
|
|
|
11.
|
A beam of unpolarized light with an irradiance
of 1000 W/m2 hits a linear polarizer whose transmission
axis is vertical. The light then passes through a second linear
polarizer with an orientation of 60o with the vertical.
What is the irradiance of the light passed by the second polaroid?
|
|
|
12.
|
Parallel rays of light of wavelength
655 nm fall upon a pair of slits that are 1.57 x 10-5
m apart. The interference pattern is focused on a screen
2.00 m from the slits. Find (a) the angle for the third maximum
and (b) the distance of this maximum from the center of the
screen.
|
|
|
13.
|
What is the relationship between the
wavelength λo in
a vacuum or air and λn
the wavelength of light in a medium of index of refraction
n?
|
|
|
14.
|
Discuss the difference for reflected
pulses on a string when the pulse goes from (a) a less dense
string to a more dense string and (b) a more dense string
to a less dense string. The speed of the pulse is greater
in a less dense string than it is in a more dense string.
|
|
|
15.
|
Light of wavelength λ
= 500 nm is incident upon a double-slit arrangement in which
the distance between the slits d = 1.00 x 10-3
m. On a screen a distance L = 1.00 m from the slits, a bright
line is observed at ym = 1.50 mm from the center
of the screen. What bright line is this, or in other words,
what is the value of m?
|
|
|
16.
|
In a double-slit interference pattern,
the distance between positions of maximum light intensity
along a distant screen is Δy
when the distance between the slits is d and the wavelength
of the incident light is λ.
If the distance between the slits is doubled and the wavelength
is halved, find the new distance between the maxima Δy’
in terms of Δy.
|
|
|
17.
|
An interference pattern for light incident
upon two slits is observed first in air and then under water.
For which case will the distance between maxima be greater?
Explain your answer.
|
|
|
18.
|
A very small source of white light is
placed at point A, above a mirror. Light can travel from A
to B by two paths, as shown in Fig. 7 below (not to scale).
Determine at least two wavelengths that will not be
present at point B. There is a 180o phase shift
on reflection at a mirror.

|
|
|
19.
|
An oil drop (n = 1.20) floating
on water (n = 1.33) is illuminated by yellow light ( λo = 580
nm) and is observed from above by reflected light.
(a) Will the outer (thinnest) regions of the drop appear bright
or dark?
(b) Find the thickness of the film for several regions where
the yellow light is observed.
|
|
|
20.
|
A soap film with n = 1.34 immersed in
air is illuminated by yellow light
( λo = 580 nm).
Find the thickness of the film for (a) a maximum and
(b) a minimum for m = 2.
|
|
|
21.
|
You are listening to a hi-fi instrument
that is in another room, and note that the lower-frequency
notes are accentuated. Explain the reason for this.
|
|
|
22.
|
Why, in our everyday experience, is the
wave nature of sound more obvious than the wave nature of
light?
|
|
|
23.
|
Figure 8 below is a graph of the intensity
of light of wavelength λ as
a function of the distance y along a screen for a single-slit
diffraction pattern with slit width a. Sketch a graph
of intensity as a function of the distance along the screen
for (a) light of wavelength λ/2
and slit width a and (b) light of wavelength λ
and slit width a/2.
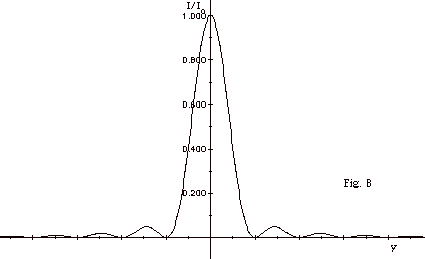
|
|
|
24.
|
A single slit 0.10 mm wide which is 2.0
m from the screen is illuminated by light of wavelength 580
nm. Find the width of the central maximum.
|
|
|
25.
|
What is the minimum distance between
two points that will permit them to be resolved at 1.00 km
using a terrestrial telescope with a 6.5 cm - diameter
objective? Take λ=
550 nm.
|
|
|
26.
|
The wavelengths of the hydrogen alpha
line and the hydrogen beta line are 653.4 nm and 580.8 nm,
respectively. If you are using a grating with 2.00 x 105
lines per meter, what is the angular separation for these
two lines in the first and third order?
|
|
|
*27.
|
Light of wavelength 600 nm is incident
normally on a diffraction grating. Two adjacent maxima occur
at angles given by sin Θ
= 0.2 and sin Θ = 0.3,
respectively. The fourth-order maxima are missing. (a) What
is the separation between adjacent slits? (b) What is the
smallest individual slit width? (c) Which orders of intensity
maxima are produced by the grating assuming the values derived
in (a) and (b)? (d) What is the ratio of the intensity of
the third maximum to the intensity of the central maximum?
|
|
|
28.
|
What angle is needed between the direction
of polarized light and the axis of a polarizing filter to
cut its intensity in half?
|
|
|
29.
|
Show that if you have three polarizing
filters, with the second at an angle of 45o with
the first and the third at an angle of 90o with
the first, the intensity of the light is reduced to 25% of
its value.
|
|
|
30.
|
At what angle will light incident from
air and reflected from diamond be completely polarized? The
index of refraction of diamond is 2.42.
|
|
|
31.
|
Light reflected at 62.5o from
a gemstone in a ring is completely polarized. Can the gem
be a diamond?
|
|