|
Review - Potential Energy, Potential,
and Capacitors
|
|
|
1.
|
Determine the electric potential due to two point charges,
Q1 and Q2, along a perpendicular
bisector at point P of the line joining the charges (Fig.
1 below). (b) What is the potential at P when r >> a?
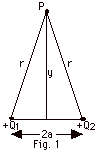
|
|
|
2.
|
Find (a) the electric potential at point
P in Fig. 2 below. (b) Find the work done in bringing up a charge
of +3 nC from infinity. (c) Repeat (a) and (b) for
q2 = +1 nC.
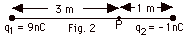
|
|
|
3.
|
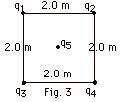
In Fig. 3 below, q1 = q2
= -200µC, q3 = q4 = +100mC
and the charge at the center of the square q5 =
+20µC. With q5 removed in Fig. 3, find
(a) the potential at the center of the square and (b) the
work done to bring q5 from infinity to the center
of the square.
|
|
|
4.
|
A positively charged particle with q
= +10-6 C and mass m = 10-3 kg is placed
between the plates of a parallel plate capacitor and is at
rest. (a) Draw the capacitor with charges, label the forces
acting on the particle, and calculate the electric field between
the plates. (b) Given the distance between the plates as
10-3 m, find the potential difference across
the plates.
|
|
|
5.
|
An alpha particle (charge +2e) approaches
a gold nucleus (charge +79e) from a very great distance, starting
with kinetic energy K. The alpha particle just touches the
surface of the nucleus (the radius of the gold nucleus is
7.0 x 10-15 m) where its velocity is reversed.
Find the initial kinetic energy of the alpha particle.
|
|
|
6.
|
A proton of mass m = 1.67 x 10-27
kg and charge q = e = 1.60 x 10-19 C is accelerated
from rest through a potential difference of 100 V. What
velocity does it achieve?
|
|
|
7.
|
Under undisturbed conditions there is
a downward-directed electric field above the surface of the
earth. If y represents the height in meters measured
from the surface, Ey, the magnitude of the field
over a limited range in y, can be represented as Ey =
- (300 V/m - 0.010y V/m2). Over the range
of validity of Ey, obtain an expression for the
potential above the surface, taking the surface to be zero
potential.
|
|
|
8.
|
In the figure below, the nonconducting
disk of radius R has a uniform charge density σ
on one surface. Find (a) the area dA of the ring of radius
r and thickness dr, (b) the charge element dq on the ring
of radius r, (c) the potential due to the ring and the potential
due to the disk at point P in the figure. (d) Find Ez
from - ΔV/ Δz.
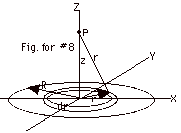
|
|
|
9.
|
A point charge q1 = +80 nC
is situated on the X-axis at the origin and a second point
charge q2 = - 60 nC is placed at x = +0.20
m, as shown in the figure below. The field point A is located
on the x-axis at x = 0.10 m. A second field point B
is in the X-Y plane at a distance of 0.16 m from q1
and 0.12 m from q2. Find (a) the potential at point
A, (b) the potential at point B, and (c) the work done in
transferring a charge of +10 µC from B to A.
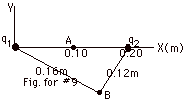
|
|
|
10.
|
Two long, thin charged wires intersect
the plane of the paper normally at A and B in the figure below.
The charge per unit length on each wire is λ.
Find the potential difference between the points C and D.
CD is the perpendicular bisector of AB. Let AC
= CB = 4.00 m, CD = 10.12 m, and AD = 10.88 m.
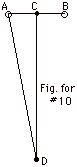
|
|
|
11.
|
Each of three parallel plate capacitors
has area A and spacing d. Find the spacing d’
of a single capacitor of plate area A if its capacitance equals
that of the three connected in (a) parallel (b) series.
|
|
|
12.
|
A spherical capacitor of radius R1
is charged to a potential difference (Vab)i.
The charging battery is then disconnected and the capacitor
is connected in parallel with a second (initially uncharged)
spherical capacitor of radius R2. The measured
potential difference drops to (Vab)f.
Find R2 in terms of R1, (Vab)i
and (Vab)f.
|
|
|
13.
|
A parallel plate capacitor has a capacitance
C when the plates have an area A, a plate separation d, and
the plates are in a vacuum. The charge on the plates is Q
when a battery of potential difference of Vab is
placed and kept across the capacitor. Find what happens to
(i) the capacitance, (ii) charge and (iii) the electric field
when (only one at a time), (a) the plate separation is doubled
and (b) a dielectric of constant k=
2 is inserted between the plates.
|
|
|
14.
|
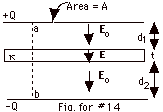
Determine the capacitance of a parallel
plate capacitor in which the region between the plates is
partially filled with a dielectric slab of thickness t and
dielectric constant k,
as shown in the figure below.
|
|
|
15.
|
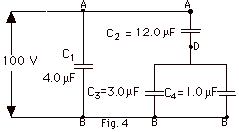
Find (a) the equivalent capacitance of
the combination of capacitors shown in Fig. 4, (b) the charge
on each capacitor, and (c) the potential difference VAD
and VDB. (d) How much energy is stored in the capacitors?
|
|
|
16.
|
Find the electric potential for a uniform
spherical charge distribution of radius R for (a) r
≥ R, (b) r ≤ R. (c) Sketch graphs
of E and V vs
r. How can you find the electric field E from a knowledge
of V(r)?
|
|
|
17.
|
A cylindrical capacitor consists of an
inner conducting cylinder of radius a with charge +Q and an
outer conducting cylinder of radius b with charge -Q. The
length L of the cylinders is great enough that the electric
field between the two cylinders is radial. Find C for
this capacitor.
|
|
|
18.
|
Parallel plates carry charges ±Q
and have a separation s. To move the plates an additional
distance ds, takes dW = F ds. (a) What is the energy U of
the plates with charge q, area A, and distance of separation
s? The work done in the separation of the plates would appear
as an increase dU in the potential energy. (b) Write an expression
for the increase in potential energy. (c) Combine all
of this to find the force required to maintain a separation
s between the plates.
|
|
|
19.
|
A spherical volume of radius R is filled
with a uniform charge density ρ.
To find the potential energy of this sphere, we find the work
to assemble it. Find (a) the charge q in a sphere of
radius r, (b) the charge q’ in a spherical shell of
radius r and thickness dr, (c) the work done U in bringing
an infinitesimal shell of thickness dr from infinity to the
radius r, (d) integrate the expression in (c) from r = 0
to r = R to find U and express it in
terms of the total charge Q in the sphere of radius R.
|
|
|
20.
|
Around 1900 a number of physicists believed
that the rest mass of the electron might be purely electrical
in origin. Using the result of Problem 19, set the potential
energy of the spherically charged volume equal to mc2
and see what you find for the radius ro of the
electron. Obviously there is a problem with the model since
no mechanism is provided to hold the charge together.
|
|
|
21.
|
A negatively charged particle of charge
q = -10-6 C and mass m = 10-10 kg travels
in an elliptical orbit around a positive charge q’ =
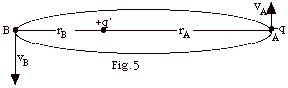
+10-6 C. When it is at A, as shown in Fig.
5 below, the distance from -q to +q is 6 x 10-5
m. When it is at B, the distance from -q to +q is 3 x 10-5
m. (a) Use conservation of angular momentum to find the ratio
of the particle's velocity at B to its velocity at A. (b) Use
conservation of energy to find va and vb.
|
|
|
22.
|
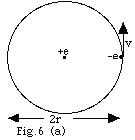
Assume that an electron of mass m moves
in a circle of radius r with a constant speed around a stationary
proton (Fig. 6a below). (a) What is the electric potential
energy of this system in terms of k, e, and r? (b) The electric
force of the proton on the electron provides the centripetal
acceleration. Use Newton's second law of motion to find mv2.
Find (c) the total energy and the angular momentum of
the system.
|
|
|
23.
|
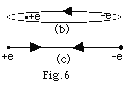
In one model of the hydrogen atom, the
electron moves in an elliptical orbit around a stationary
proton. For the very "skinny" ellipse of Fig. 6b
below, the electron's motion can be approximated by motion
back and forth along a straight line (Fig. 6c below). Find
(a) the electric potential energy of the system when the electron
is a distance 2r from the proton and (b) the kinetic energy
of the system when the electron is at this distance. (c) Compare
the total energy and the angular momentum of the system with
the model of Problem 22.
|
|
|
24.
|
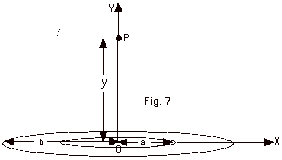
An insulating washer (Fig. 7) carries
charge Q uniformly distributed along its surface. Find (a)
the potential V at point P a height y above the surface, (b)
the electric field at point P (magnitude and direction) and
(c) the electric field at O.
|
|
|
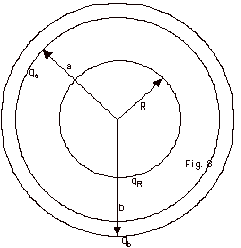
25.
|
A conducting sphere with radius R carrying
a charge qR is surrounded by a spherical shell
with inner radius a and outer radius b, as illustrated in
Fig. 8 below. The outer surface of the shell has a charge
qb = 6 µC and its inner surface has charge
qa = 5 µC.
(a) Find qR and explain how you found
it.
(b) Find E as a function of r for (i) 0 < r < R, (ii)
R < r < a,
(iii) a < r < b, and (iv) r
> b.
(c) Sketch a graph of (i) E versus r, and (ii) V versus
r.
|
|
|
26.
|
In Figure 9, an infinite line carries
a charge per unit length λ.
The point P is distance a from the infinite line and is grounded
so that V(a) = 0.
(a) Find V(r) for r < a. (b) Explain why you cannot
take a = infinity, and (c) verify that Er
= -dV/dr.
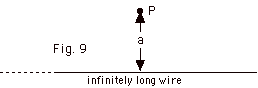
|
|
|
27.
|
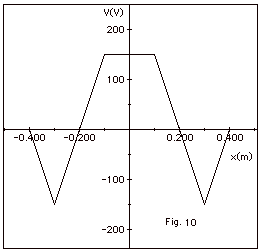
Figure 10 is a graph of electric field
as a function of x. Plot V as a function of x. Ignore the
points on the graph where there are discontinuities.
|
|