|
Answers - Electric Fields
|
|
|
1.
|
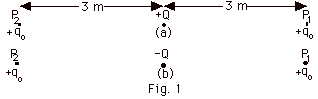
- The magnitude of the force of +Q or -Q on qo
at r = 3 m is FqQ = kQqo/r2
= (9.0 x 109 N-m2/C2)(2
x 10-6 C)(10-12 C)/(9 m2)
= 2 x 10-9 N.
The force of +Q on +q0 at
- P1 is to the right since +Q repels +qo
and urges it to the right
- P2 is to the left since +Q repels +qo
and urges it to the left.
- The force of -Q on + qo at
- P1 is to the left since -Q attracts +qo
and urges it to the left
- P2 to the right since -Q attracts +qo
and urges it to the right.
|
|
|
2.
|
By definition, the direction of the electric field is the
direction in which a positive test charge is urged. The magnitude
of the electric field at a point P is equal to the electric
force Fe on a test charge qo divided
by the test charge.
For all points in Fig. 1 above, the magnitude of the electric
field = (Fe)/qo = (kQqo/r2)/qo
= kQ/r2 = (9 x 109 N-m2/C2)(2
x 10-6 C)/9 m2 = 2 x 103 N/C.
- In Fig. 1a, the electric field at P1 is to
the right because a positive test charge there would be
urged to the right. At P2 the electric
field is to the left because a positive test charge there
would be urged to the left.
- In Fig. 1b, the electric field at P1 is to
the left because a positive test charge there would be urged
to the left. At P2 the electric field is
to the right because a positive test charge there would
be urged to the right. Do not use the sign of a charge setting
up a field to determine the direction of a field. Go to
the point, imagine placing a positive test charge there,
and ask what direction the test charge would be urged by
the charge setting up the field.
|
|
|
3.
|
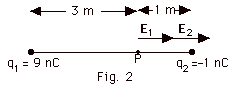
- In general the electric field E due to a point charge
Q a distance r from the point where you wish to find the
field is given by
E = (9 x 109 N-m2/C2)Q/r2.
For q1 in Fig. 2, E1 = (9 x 109
Nm2/C2)(9 x 10-9 C)/(3
m)2 = 9 N/C to the right because if a positive
test charge is placed at P, q1 would urge it
to the right. E2 = (9 x 109 N-m2/C2)(1
x 10-9 C)/ (1 m)2 = 9 N/C to the right
because if a positive test charge is placed at P, q2
would urge it to the right. The resultant field at P is
E = (9 + 9) N/C = 18 N/C to the right. Again notice
the importance of not using the negative sign of the charge
in finding the field. If you had used the negative sign,
you might have said the field due to q2 was to
the left.
- If q2 = +1 nC, the electric field
due to q2 at P is 9 N/C to the left. Now taking
to the right as positive, the resultant field at P is E
= (9 - 9) N/C = 0.
|
|
|
4.
|
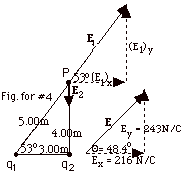
In Fig. for #4 above, the hypotenuse of the triangle = (9.00
+ 16.00)1/2 m = 5.00 m.
The field due to q1, E1 =
q1/4πεor12
= 9 x 109 N-m2/C2(10-6
C/25.0m2)
= 360 N/C. The direction of E1 is
shown in Fig. for #4.
E2 = 9 x 109 N-m2/C2(0.0800
x 10-6 C/16.00 m2) = 45 N/C, and
E2 = -45 j N/C, as
shown in Fig. for #4.
Taking components of E1, (E1)
x = E1 cos 53o = 360 N/C (0.60)
= 216 N/C,
and (E1)y = E1 sin 53o=
360 N/C (0.80) = 288 N/C. The component of the resultant
E in the y direction Ey = (E1)y
+ (E2)y = (288 - 45) N/C = 243 N/C.
E = (216 i + 243 j)N/C. E
= {(216)2 + (243)2}1/2 =
325 N/C.
tan Θ = 243/216.
Θ = 48.4o with
X-axis.
|
|
|
5.
|
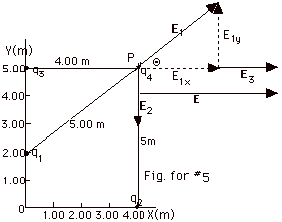
- In the Fig. for #5 above, E1 represents
the electric field due to
q1 = 5.00 x 10-6 C, which is
r = 5.00 m from P.
E1 = kq1/r2 = 9 x 109
N-m2/C2 (5.00 x 10-6C)
25.0 m2
= 1.80 x 103 N/C.
E1x = E1 cos Θ=
1.80 x 103 N/C (0.800) = 1.44 x 103 N/C.
E1y = E1 sin Θ=1.80
x 103 N/C (0.600) =1.08 x 103 N/C.
In the Fig. for #5 above, E2 represents
the electric field due to
q2 = -3.00 x 10-6 C, which is a distance
of r2 = 5.00 m from P.
E2 = kq2/r2 = 9 x 109
N-m2/C2 (3.00 x 10-6)/25.0
m2 = 1.08 x 103 N/C
in the negative Y direction (Fig. for #5).
E2x = 0 and E2y = -1.08 x 103
N/C.
In the Fig. for #5, E3 represents
the electric field due to
q3 = 1.60 x 10-6 C, which is a distance
of r3 = 4.00 m from P.
E3 = kq3/r3 = 9 x 109
N-m2/C2 (1.60 x 10-6)/16.0
m2 = 0.900 x 103 N/C
in the positive X direction as shown in Fig. for #5.
E3x = 0.900 x 103 N/C and
E3y = 0.
Let the total electric field = E.
Ex = E1x + E2x + E3x
= (1.44 + 0 + 0.90)103 N/C = 2.34 x 103
N/C.
Ey = E1y + E2y + E3y
= (1.08 -1.08 + 0)103 N/C = 0. The resultant
electric field is totally in the +X direction and it is
equal to 2.34 x 103 N/C.
- Electric force on q4 = q4E = 2.0
x 10-6 C(2.34 x 103 N/C) =
4.68 x 10-3 N.
|
|
|
6.
|
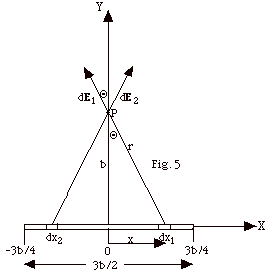
- λ = charge/length
so that charge = λ(length)
or dq = λ dx.
- Treating dq as a point charge, dE = k ( λ
dx)/r2.
- The direction of an electric field is that in which a
positive test charge is urged. If a positive test charge
were at P, it would be urged up along the line connecting
dq and P.
dE1 due to the charge at dx1
and dE2 due to the charge at dx2
are as shown in Fig. 5 above.
As shown in the figure, the X-components of these two elements
of electric field cancel. The resultant direction of the
electric field due to these two elements of charge or any
other two symmetrically displaced elements will be in the
positive Y-direction.
- The magnitude of the component of dE in the Y-direction
dEy = dE cos Θ=
k λdx cos Θ/r2.
- Only b is constant. The quantities x, r, and Θ
are variables.
- x = b tan Θ and
dx = b sec2 Θ dΘ.
- r2 = b2 + x2 = b2
+ b2 tan2 Θ
= b2(1 + tan2 Θ)
= b2 sec2 Θ.
dEy = λkdx
cos Θ/r2 =
λkb sec2
Θ dΘ
cos Θ/b2 sec2
Θ= λkdΘ
cos Θ/b.
- When x = - 3b/4, r = [b2 + (-3b/4)2]1/2
= b[16/16 + 9/16]1/2 = 5b/4,
which is also true for x = +3b/4.
For lower limit, sin Θ= (-3b/4)/(5b/4) = - 3/5.
For the upper limit, sin Θ =
(3b/4)/(5b/4) = 3/5.
- ∫ λk dΘ
cos Θ/b = k λ
sin Θ/b.
Putting in the lower and upper limits, Ey = k λ/b
[3/5 - (-3/5)] = 6k λ/5b.
|
|
|
7.
|
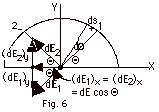
The charge on an arc of length ds is
dq = λds,
where λ is the charge per
unit length. If the arc length subtends an angle dΘ
in a circle of radius R,
dq = λ(ds) =
λ(R dΘ).
The electric field at a point P due to an element of length
ds1 is
dE1 = dq/4πεoR2
= λo
cos ΘR dΘ/4πεoR2.
The electric field dE2 at point P due to an
element of length ds2 has the same magnitude
as that of dE1, but not the same direction
as dE1, as illustrated in Fig. 6 above.
Since cos (180o - Θ)
= - cos Θ the charge
is negative in quadrant 2. dE2 is in
towards the arc.
Components of the dE's in the Y direction cancel. Components
in the X direction are equal and add.
(dE1)x = (dE2)x
=
dE1 cos Θ = λo
dΘ (cos2 Θ)/R
= ( λo dΘ
/4πεoR)(1/2 +
1/2 cos 2Θ)dΘ.
The total electric field is to the left and 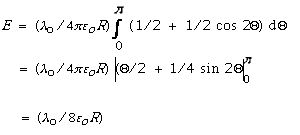
|
|
|
8.
|
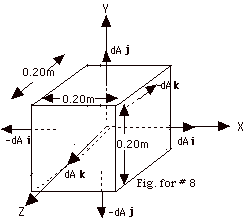
We must find the flux = ∫E •
dA leaving the sides of the cube.
For all cases E = 100 N/C-m xi.
For the right and left sides, dA = ±dA
i and
∫ E • dA = (100 N/C-m)[(∫xi
• dAi + ∫xi
• -dAi)
=
(100 N/C-m)[∫0.1m dA + ∫(-0.1m)(-dA)]
=
(100N/C)[0.1m(0.04 m2)+(-0.1m)(-0.04 m2)]
= 0.8 N-m2/C, since
i • i = 1,
x = +0.1m on the right hand side,
x = -0.1m on the right hand side, and
∫dA = (0.20 m x 0.20 m) = 0.04 m2.
For the top and bottom sides,
∫E • dA =
(100 N/C-m)(∫xi • dAj
+ ∫xi • -dAj)]
= 0, because i • j = 0.
For the front and back sides,
∫E • dA =
(100 N/C-m)(∫xi • dAk
+ ∫xi • -dAk)
= 0, because i • k =
0.
For all sides, ∫ E . dA = 0.8
N-m2/C = charge enclosed/ εo
0.8
N-m2/C = Q/(8.85 x 10-12 C2/N-m2).
Q = 0.8 C(8.85 x 10-12) = 7.1 x 10-12 C.
|
|
|
9.
|
For spherical symmetry, the electric
field at P must remain constant at point P despite the rotation
of the sphere inside the Gaussian surface. If this is
to be true,
- the electric field can not depend on angles Θ and
Φ,
- the only possible direction for E is radially
outward (or inward for negative charge),
- the magnitude of the electric field must be constant
everywhere on the Gaussian surface.
- For E radially outward,
 E,
dA = 0 and E,
dA = 0 and
E • dA = E dA cos  E,
dA = E dA cos 0o = E dA. E,
dA = E dA cos 0o = E dA.
- If E is constant, ∫E dA = E ∫ dA = E 4 πr2,
where 4 πr2
= the surface area of the Gaussian spherical surface
of radius r.
|
|
|
10.
|
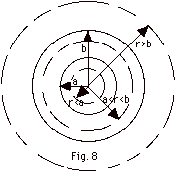
In Fig 8 above, the dashed surfaces represent the Gaussian surfaces
and the solid lines represent the spherical charged shell of
inner radius a and outer radius b.
- charge/volume = ρ
= Q/[(4 π/3)(b3
- a3)], where the volume of the spherical shell
is the difference between the volumes of a sphere of radius
b and a sphere of radius a.
-
- For r < a, no charge is enclosed.
- For a < r < b, the Gaussian surface
has a volume
(4 π/3)(r3
- a3)
and encloses an amount of charge =
ρ(4 π/3)(r3
- a3) =
[Q/(4 π/3)(b3
- a3)](4 π/3)(r3
- a3) =
Q(r3 - a3)/(b3
- a3).
- For r > b, the Gaussian surface encloses
the total charge Q.
- For each of the Gaussian surfaces,
 E,
dA = 0 and E •
dA = E dA. E,
dA = 0 and E •
dA = E dA.
Also E is constant everywhere on the Gaussian surface, so
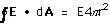 .
.
For all cases then, E 4 πr2
= charge enclosed/ εo.
- For r < a,
E 4 πr2
= 0
E
= 0
- For a < r < b,
E 4 πr2
= Q(r3 - a3)/ εo(b3
- a3)
E
= Q(r3 - a3)/4πεor2(b3
- a3)
- For r > b,
E 4 πr2
= Q/ εo
E
= Q/4πεor2
- For r = a, E = Q(a3 - a3)/4πεor2(b3
- a3) = 0 = E
For r = b, E = Q(r3 - a3)/4πεor2
(b3 - a3) = Q/4πεob2
For r = b, E = Q/4πεor2
= Q/4πεob2
Thus,
- For r ≤ a,
E = 0
- For a ≤ r ≤ b,
E = Q(r3 - a3)/4πεor2(b3
- a3)
- For r ≥ b,
E = Q/4πεor2
|
|
|
11.
|
- The circumference of the base equals 2 πr,
where r is the radius of the base. If you roll the
cylinder out, it becomes a rectangular parallelepiped with
width 2 πr and length
L. Its area is the width times the length or 2 πrL.
- The volume of the cylinder is the area of the base πr2
times the length L, or πr2L.
|
|
|
|
|
13.
|
If you rotate the dipole inside the spherical
Gaussian surface, the electric field at a fixed point on the
Gaussian surface would change. You cannot use a spherical Gaussian
surface nor any other type of surface such that the electric
field would preserve the symmetry. Thus you cannot use Gauss's
theorem to find the electric field of a dipole.
|
|
|
14.
|
- For r = 0.5 m, E = 144 N/C. For r
= 1.0 m, E = 72 N/C.
As you double r, E is halved.
E must be inversely proportional to r, that is, E
∝1/r.
This corresponds to the field being set up by a long cylinder
of charge.
- For r = 0.5 m, E = 144 N/C. For r
= 1.0 m, E = 36 N/C.
As you double r, E is reduced by a factor of four.
E must be inversely proportional to the square of r, that
is, E ∝1/r2.
This corresponds to the field outside a charged sphere.
- For r = 0.5 m and r = 1.0 m, E
= 144 N/C. The electric field is constant regardless
of the distance from the charge distribution.
This corresponds to the field set up by an infinite sheet
of charge.
- The field outside a sphere with charge q is E = kq/r2.
q = Er2/k = (144 N/C)(0.25 m2)/(9.0
x 109 N-m2/C2) = 4.0 x
10-9 C.
- For a cylinder, E = λ/2πεor
or
λ= 2πεo
rE =
2 π(8.85 x 10-12
C2/N-m2)(0.5 m) (144 N/C) =
4.0 x 10-9 C/m.
- For an infinite sheet of charge, E = σ/2 εo
or
σ = 2 εo
E = 2(8.85 x 10-12 C2/N-m2)(144
N/C) = 2.55 x 10-9 C/m2.
|
|
|
15.
|
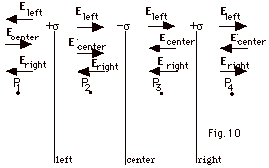
The electric field due to an infinite sheet of charge is
σ/2 εo.
The direction of an electric field at a point P is that in which
a positive test charge placed at that point would be urged.
As shown in Fig. 10 above,
- At point P1 the electric field due to the sheet
on the left Eleft is to the left, the
electric field due to the center sheet Ecenter
is to the right, and the electric field due to the
sheet on the right Eright is to the left.
Taking to the right to be positive, the electric field is
to the left with magnitude E (at P1) equals
-σ/2 εo
+ σ/2 εo
- σ/2 εo
= - σ/2 εo.
- At point P2 the electric field due to the sheet
on the left Eleft is to the right, the
electric field due to the center sheet Ecenter
is to the right, and the electric field due to the
sheet on the right Eright is to the left.
Taking to the right to be positive, the E is to the
right with magnitude E (at P2) equals
+σ/2 εo
+ σ/2 εo
- σ/2 εo
= +σ/2 εo
.
- At point P3 the electric field due to the
sheet on the left Eleft is to the right,
the electric field due to the center sheet Ecenter
is to the left, and the electric field due to the
sheet on the right Eright is to the left.
Taking to the right to be positive, the electric field is
to the left with magnitude E (at P3) equals
σ/2 εo
- σ/2 εo
- σ/2 εo
= - σ/2 εo
.
- At point P4 the electric field due to the sheet
on the left Eleft is to the right, the
electric field due to the center sheet Ecenter
is to the left, and the electric field due to the
sheet on the right Eright is to the right.
The electric field is to the right with magnitude E (at
P4) equals
σ/2 εo
- σ/2 εo
+ σ/2 εo
= +σ/2 εo
.
|
|
|
16.
|
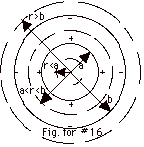
In the figure above, the Gaussian surfaces for r <
a, a < r < b, and r > b
are shown by dashed surfaces.
Using the same arguments we did in Problem 10, we establish
that the electric field is perpendicular to the Gaussian surfaces
and constant everywhere on them.
The definition of a conductor is that charges are perfectly
free to move in them. They move until there is no electric
field inside the conductor that would produce a motion of
charges. Since there is no electric field inside the sphere
of radius a, there can be, in agreement with Gauss' theorem,
no charges enclosed by a surface inside the sphere. That
is, if
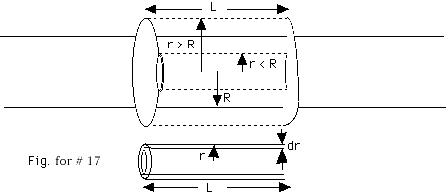
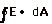 = (0)4 πr2 =
charge enclosed/ εo
,
= (0)4 πr2 =
charge enclosed/ εo
,
the charge enclosed must equal zero.
You can use this argument until r goes to a and decide the +Q
is on the outside of the sphere of radius a. In addition,
since there can be no charges inside of the spherical shell,
the - Q must be on the inner surface of the spherical shell,
as shown in the above figure.
(a) From all of this we conclude that for r < a, E
= 0.
The Gaussian surface with radius r such that a < r
< b, encloses +Q.
By Gauss' theorem,
E 4 πr2
= charge enclosed/ εo.
(b) For a < r < b,
E(4 πr2)
= Q/ εo
E = Q/4πεor2
= kQ/r2
(c) For r > b, charge enclosed = + Q - Q = 0
so
E(4 πr2)
= 0 or
E = 0.
|
|
|
17.
|
From Gauss' theorem, 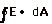 = charge enclosed/ εo
.
= charge enclosed/ εo
.
By symmetry conditions,  E,
dA = 0 and E is constant everywhere
along the Gaussian surface. So for both r > R
and r < R, E,
dA = 0 and E is constant everywhere
along the Gaussian surface. So for both r > R
and r < R, 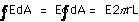 . .
The charge enclosed by the Gaussian surface will differ for
r < R and r > R.
For r > R, the Gaussian surface will enclose
the total charge in a cylinder of length L. Since the
density of charge ρis a
function of r, we need to find an expression for the charge
enclosed. Because the density of charge ρ
= charge/volume, for a volume dV, the charge enclosed dq = ρ
dV. We must find the volume dV of a cylindrical shell of length
L radius r and thickness dr, as shown in the lower drawing in
Fig.11 above. If you slit this shell and rolled it out, you
would have a plate of width 2 πr,
length L, and thickness dr. Thus dV = 2 πrL
dr.
- For r < R,
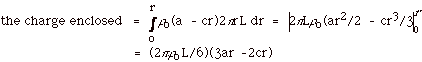
For r < R, Gauss's theorem gives
E2 πrL = (2πρoL/6 εo)(3ar2
- 2cr3), and
E = (ρo/6 εo)(3ar
- 2cr2).
- For r > R,
charge enclosed is found by using limits for the above integral
of 0 and R. Charge enclosed = (2πρoL/6)
(3aR2 -2cR2), and
now
E2 πrL =
(2πρoL/6 εo)(3aR2
-2cR3), and
E = (ρo/6r εo)(
(3aR2 -2cR3)
The expression of E for r < R at r = R
reduces to E = (ρo/6 εo)(3aR
- 2cR2), as does the expression of E
for r > R.
|
|
|
18.
|
The
tangent to an electric field line at a point gives the direction
of the electric field at that point. If two field lines intersect
at that point, then the electric field would have two different
directions at that point. Since this is impossible, electric
field lines cannot intersect.
|
|
|
19.
|
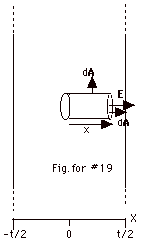
- Because there is equal amount of positive charge on the
sheet from
x = - t/2 to x = t/2, the electric field at x
= 0 is 0. By symmetry and the definition of
the direction of an electric field, the electric field is
to the right for x > 0 and to the left for x < 0.
For the cap of the "beer can" Gaussian surface,
 E,
dA = 0. E,
dA = 0.
For the lateral surface  E,
dA = 90o. E,
dA = 90o.
For the cap, E . dA = E dA.
For the lateral surface, E . dA
= 0.
By Gauss's theorem, E dA = charge enclosed/ εo
= xdA ρ/ εo
and E = ρx/ εo.
- The force on the negative charge q = Eq = -(ρq/ εo)x,
where the minus sign means the force is opposite to
the displacement x. The quantities in the parenthesis
(ρq/ εo)
are constant, so this is an example of simple harmonic motion.
Fnet
= ma or
-(ρq/ εo)x
= m d2x/dt2 or
d2x/dt2 + (ρq/m εo)x
= 0.
Compare with
d2x/dt2 + (k/m)x = 0,
for which the frequency f = 1/2 π
(k/m)1/2
and see for this case f = 1/2 π
(ρq/m εo)1/2.
|
|
|
20.
|
| X |
Y |
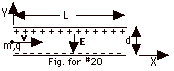 |
| xo =
0 |
yo
= 0 |
| vox = v |
voy = 0 |
| ax = 0 |
ay = Fy/m
= eE/m, with ay up |
| x
= L = vt or
t = L/v (Equation
1) |
| y = 1/2 ayt2
= d/2 = 1/2 qE/m t2 (Equation
2) |
Substituting Eq. 1 into Eq. 2:
d/2 = 1/2 eE/m (L/v)2 or v = L(eE/dm)1/2.
|
|
|
21.
|
Electric field E due to the long wire
at a distance r = λ/2πεor
and the force on the electron with charge e is F = eE = e λ/2πεor
radially inward. This force produces a centripetal acceleration
such that
Fnet =
ma
e λ/2πεor
= mv2/r or
v = (e λ/2 πm εor)1/2
= [1.6 x 10-19 C(2.5 x 10-9 C/m)/2 π(9.1
x 10-31 kg)(8.85 x 10-12 C2/N-m2)]1/2
= 2.8 x 106 m/s.
|
|
|
22.
|
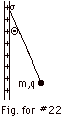
The electric force on the sphere of charge q is Fe
= qE. The electric field due to the sheet E = σ/2 εo.
For the sphere to remain at rest, the net force
on it must equal zero, that is T + mg + qE
= 0, where T is the tension in the string.
From the geometry of the figure above, we see that
tan Θ = qE/mg = (qσ/2 εo)/mg
or
σ = 2 εomg
tan Θ/q.
|
|
|
23.
|
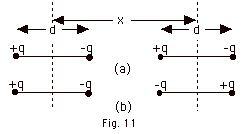
Taking to the right to be positive for the force of the charges
in the dipole at the left on the charges in the dipole at the
right in Fig. 11a above,
F = kq2/x2 - kq2/(x +d)2
- kq2/(x - d)2 + kq2/x2
Putting the above expression over the common denominator
x2(x2 + d2) (x2
- d2) gives:
F = {kq2/[ x2(x + d)2 (x
- d)2]}{2(x + d)2 (x - d)2
- x2(x - d)2 - x2(x +d)2}
= {kq2/[ x2(x2
- d2)2} {2(x2 – d2)2
- x2(x - d)2 - x2(x +d)2}
= {kq2/[ x2(x2
- d2)2} {2(x4 – 2x2d2
+ d4) - x2(x2 - 2dx + d2)
- x2(x2
- 2dx + d2)}
= {kq2/[ x2(x2
- d2)2} {-6x2d2 +
2d4}
Since 6x2d2 > 2d4, the
net force on the dipole to the right will be to the left.
By Newton's third law, the net force on the dipole to the
left will be equal in magnitude, but to the right.
For Fig. 11b, again taking to the right to be positive for
the forces of the charges in the dipole at the left on the
charges of the dipole at the right,
F = = -kq2/x2 + kq2/(x +d)2
+ kq2/(x -d)2 - kq2/x2.
The magnitude of the force is the same as in (a), but opposite
in direction. Notice for x >> d, |F| = |{kq2/[
x2(x2 - d2)2}
{-6x2d2 + 2d4}|
reduces to 6kq2d2/x4 = 6kp2/x4,
where p = the dipole moment.
|
|
|
24.
|
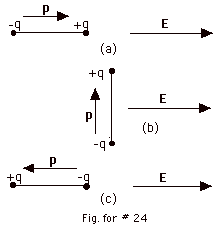
In general the torque τ=
p x E
τ = pE sin  p,
E p,
E
- For p parallel to E (Fig. for 24a above)
 p,
E = 0, sin 0o = 0, so τ= 0. p,
E = 0, sin 0o = 0, so τ= 0.
- For p perpendicular to E (Fig. for 24b
above)
 p,
E = 90o, sin 90o = 1,
so τ= pE =[qd](E) p,
E = 90o, sin 90o = 1,
so τ= pE =[qd](E)
=
[(3.2 x 10-19 C)(2 x 10-9 m)](5.0
x 105 N/C)
=
3.2 x 10-22 N-m.
The direction of the torque is into the page.
- For p antiparallel to E (Fig. for 24c
above)
 p,
E = 180o, sin 180o = 0,
so τ= 0. p,
E = 180o, sin 180o = 0,
so τ= 0.
|
|
|
25.
|
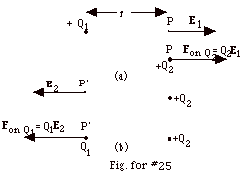
In Fig. for #25(a), we think of Q1 setting up a field
E1 at P, where E1 = kQ1/r2
to the right. When Q2 is placed at P, it experiences
a force Fon Q2,
where Fon Q2 = Q2E1 = kQ1Q2/r2
to the right.
In Fig. for #25(b), we think of Q2 setting up a field
E2 at P’, where E2 = kQ2/r2
to the left. When Q1 is placed at P’,
it experiences a force Fon Q1,
where Fon Q1 = Q1E2
= kQ1Q2/r2 to the left.
This is the same result of the force on Q2 due to
Q1 and the force on Q1 due to Q2
found from Coulomb's law.
|
|
|
26.
|
- You can find an electric field due to a distribution of
charges by
- treating dq as a point charge, taking components of
the electric field, and then integrating, or
- using Gauss's theorem if the charge distributions
has spherical, cylindrical, or plane symmetry.
- Once you know an electric field E, you can find
the electric force Fe on a charge q from
Fe = qE.
|
|
|
|
|