|
Answers - Geometric Optics
|
Note
that I have used:
so = object distance, si
= image distance,
Θi
for the incident ray, Θr
for the reflected ray, Θt
for the transmitted ray. |
|
|
1.
|
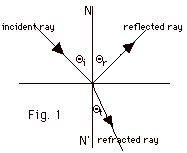
The angle of incidence Θi
is the angle between the incident ray and the normal N. The
angle of reflection Θr
is the angle between the reflected ray and the normal N. The
angle of refraction (transmission) Θt
is the angle between the refracted ray and the normal N’.
|
|
|
2.
|
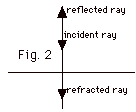
When a light ray hits a surface normally, the angle between
the incident ray and the normal is 0, so Θi
= 0. Since the angle of reflection equals the angle of
incidence, Θr=
0. By Snell's law, ni sin Θi
= nt sin Θt.
For any value of ni and nt, if Θi
= 0, Θt
= 0.
|
|
|
3.
|
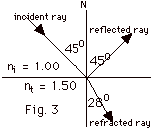
- The angle of incidence, the angle between the incident
ray and the normal N is given as 45o. Since the
angle of reflection equals the angle of incidence, the angle
of reflection is 45o.
- By Snell's law
ni
sin Θi
= nt sin Θt
1.00 sin 45o = 0.707 = 1.50 sin Θt.
sin Θt
= 0.707/1.50 = 0.471. Θt
= 28o
|
|
|
4.
|
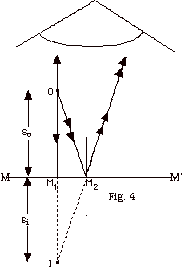
Ray 1, designated by one arrow, hits the mirror normally and
is reflected back on itself, as shown in Fig. 4.
Ray 2, designated by two arrows hits the mirror at some angle
of incident greater than zero and is reflected back at the same
angle. If you dash the reflected rays behind the mirror, you
see that they meet at a point that I have labeled I for image.
The big eye seen at the top of the figure sees the two reflected
rays as though they have originated at the image. In other words,
if you sight along the two reflected rays they appear to have
come from the image. This image is called a virtual image because
the rays do not actually meet at that point.
The distance of the object O from the mirror, so ,
is called the object distance and the distance of the
image I from the mirror, si , is
called the image distance. If you measure them or use geometry
to calculate the distance si, you find that si
equals so for a plane mirror.
By geometry,
 M1OM2
= Θi (alternate
interior angles), M1OM2
= Θi (alternate
interior angles),
 OIM2
= Θr (two
parallel lines crossed by a line), OIM2
= Θr (two
parallel lines crossed by a line),
and the angle of incidence = the angle of reflection.
Triangles OM1M2 and IM1M2 are
congruent (all angles are equal and they have a common side).
Thus, so = si.
|
|
|
5.
|

Using Snell's law to find the angle of refraction, 1.00 sin
37o = 1.50 sin Θt.
Θt = 23.6o.
The angle of transmission and the angle of incidence on the
interface between the glass and the air are equal (a line cut
by two parallel lines). Since Θi
= 23.6o at the glass-air interface = Θt
at the initial air-glass interface, the angle of refraction
at the glass-air interface is 37o from Snell's law.
I have dashed the incident ray to show you that for a parallel
plate, the refracted beam is parallel to the incident beam.
This tells you that for a very thin parallel plate, the incident
beam passes through without any deviation, as with a thin lens.
|
|
|
6.
|
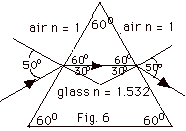
Using Snell's law,
ni sin Θi
= nt sin Qt.
At first interface,
1(sin 50o) = 1.532 sin Θt
sin Θt = 0.766/1.532
= 0.500. Θt
= 30o.
At the second interface, as the light ray is going from the
glass back into the air, Θ’i
= 30o . Now Θ’t
= 50o. The path of the ray is shown in Fig.
6 above.
For 1 sin 50o = n’ sin Θt ,
with n’ less than 1.532, Θt’
would be greater than 30o. The light for λ’
would be bent less toward the normal. When the ray goes from
the prism back into the air, n’ sin Θ'i
= 1 (sin Θ’t)
and the light ray would be bent less away from the normal than
the light for λ. The overall
effect is that the light of wavelength λ’
has a smaller deflection from the original direction of the
incident beam than light of wavelength λ.
|
|
|
7.
|
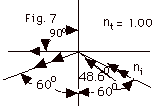
- The angle of refraction Θt
= 90o.
- ni sin Θi
= nt sin Θt
ni sin 48.6o = 1.00 (sin 90o)
ni = 1/0.750 = 4/3
- For Θi
= 60o, 4/3 sin 60o = (1.00)
sin Θt.
sin Θt =
4/3 (0.866) = 1.15, which is not possible because the maximum
value of a sine is 1. What happens is that the ray is totally
internally reflected as shown in Fig. 7 above with the rays
with two arrows.
|
|
|
8.
|
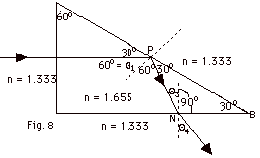
- From the geometry of the prism, we see that Θ1
= 60o and Θ3
= 30o.
(In triangle PBN, there are 180o = (30o
+ 30o + 90o + Θ3).
From Snell's law,
1.655 sin Θ3
= 1.333 sin Θ4
(1.655)(0.5000) = 1.333 sin Θ4
Θ4
= 38.4o.
- Total internal reflection occurs when 1.655 sin Θ1
> nmix sin 90o.
Total internal reflection ceases when 1.655 sin 60o
= nmix sin 90o = (nmix)(1).
nmix = 1.655 (0.866) = 1.433.
|
|
|
9.
|
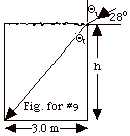
ni sin Θ1
= nt sin Θt.
Θi =
90o - 28o = 62o.
1.00 sin 62o = 1.33 sinΘt.
sinΘt = 1.00(0.883)/1.33
= 0.664.
Θt = 41.6o.
tan Θt = 0.888
= 3.0 m/h.
h = 3.38 m.
|
|
|
10.
|
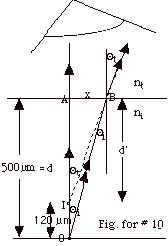
Ray 1 (indicated with one arrow in Fig. for #10) from the scratch
at O hits the surface of the slip normally at an angle of incidence
of 0o and continues into the air with no refraction.
Ray 2, (indicated with two arrows) is incident upon the surface
of the slip at angle Θi
and transmitted at angle Θt.
The camera or an eye sees these two rays as though they had
diverged from the image I.
From the geometry of the figure, we see that tan Θt
= x/d’ and tan Θi
= x/d.
From Snell's law,
ni sin Θi
= nt sin Θt.
For sin Θ approximately
equal to tan Θ, Snell's
law becomes
ni tan Θi
= nt tan Θt.
Or,
since tan Θt
= x/d’ and tan Θi
= x/d, ni x/d = nt x/d’.
Thus, ni/nt = d/d’.
Putting in nt =1.00, d = 500 µm, and d’
= 500 µm - 120 µm = 380 µm,
ni /1 = 500 µm/380 µm = 1.32.
|
|
|
11.
|

ni sin Θi
= nt sin Θt.
For the ray incident at the top of the semicircle (Fig.
9),
ni = 1, nt = 4/3, and Θi
= 53o.
From Snell's law,
(1) sin 53o = 4/3 sin Θt
or
(1)(4/5) = 4/3 sin Θt,
sin Θt = 3/5
and Θt
= 37o.
The transmitted ray travels along a radius, hits the interface
between "water and air" normally, and experiences
no refraction as it goes into the air.
|
|
|
12.
|
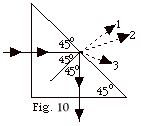
- From the geometry of Fig. 10 above, the angle of incidence
at the interface between the prism and air is 45o.
For a minimum index of refraction np of the prism,
np sin 45o = nair
sin 90o or
np = 1/sin 45o = 1.41.
- If the index of refraction is too small, the refracted
ray will be #3 since it bends away from the normal. Ray
1 is the normal and Ray 2 bends toward the normal.
|
|
|
13.
|
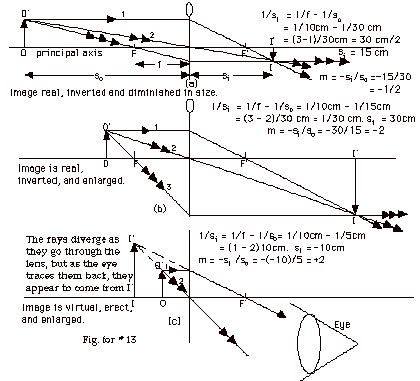
- 1/si = 1/f - 1/so = 1/10 cm - 1/30
cm = (3 - 1)/30 cm.
si = 15 cm.
m = -si/so = -15 cm/30 cm = -1/2.
The image is real, inverted, and diminished in size.
- 1/si = 1/f - 1/so = 1/10 cm - 1/15
cm = (3 - 2)/30cm.
si = 30 cm.
m = -si/so = -30 cm/15 cm = -2.
The image is real, inverted, and enlarged in size.
- 1/si = 1/f - 1/so = 1/10 cm - 1/5
cm = (1 - 2)/10 cm.
si = -10 cm.
m = -si/so = +10 cm/5 cm = +2.
The image is virtual, erect, and enlarged in size.
|
|
|
14.
|
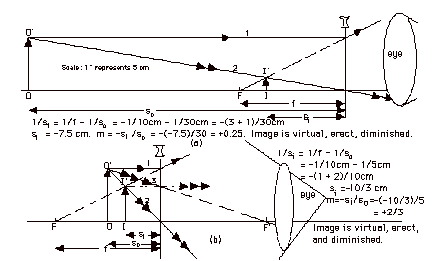
- 1/si = 1/f -1/so
= 1/10 cm -1/30 cm = - (3 + 1)/30 cm.
sI = -7.5 cm.
m = -si/so = - (-7.5 cm)/20
cm = +0.25.
Image is virtual, erect, diminished.
- 1/si = 1/f -1/so
= 1/10 cm -1/5 cm = - (1 + 2)/10 cm.
sI = -10/3 cm.
m = -si/so = - (-10/3 cm)/5
cm = +2/3.
Image is virtual, erect, diminished. See ray diagram
in figure above.
|
|
|
15.
|
With a single converging lens, a virtual
image is never inverted, so the image in this problem must be
real.
The magnitude of the magnification = 3.0 cm/1.0 cm = si/so
or
si/100 cm = 3 and
si = +300 cm since it is a real image. 1/so
+ 1/si =
1/100 cm + 1/300 cm = 4/300 cm = 1/f. f = 75 cm.
|
|
|
16.
|
6.0 cm/2.0 cm = si/so
= si/8.0 cm or the magnitude of si =
24 cm.
Since it is a virtual image, we take si = -24 cm.
1/so + 1/si = 1/8.0 cm - 1/24 cm = (3
- 1)/24 cm = 1/12 cm = 1/f.
f = 12 cm.
|
|
|
17.
|
Magnitude of the magnification = 95/5
=19 = si/so or
19so = si (Equation
1)
For the projector, the image is real. so +
si = 4.00 m = 400 cm. (Equation
2)
Substituting Eq. 1 into Eq. 2:
so + 19 so = 20 so = 400 cm.
so = 20 cm; si = 380 cm.
1/so + 1/si = 1/20 cm + 1/380 cm = 20/380
cm = 1/f.
f = 19 cm.
|
|
|
18.
|
For virtual image, si
< 0. 1/so + 1/si = 1/12
cm - 1/6 cm = -1/12 cm = 1/f.
f = -12 cm. f is negative, which corresponds to a diverging
lens.
|
|
|
19.
|

- Calculate the position of the first image.
1/si1 = 1/f1 - 1/so1 =
1/2.0cm - 1/2.2cm. si1 = 22 cm.
For minimum eyestrain, the eyepiece is adjusted so that
parallel rays emerge, and hence this image is at the focal
point of the eyepiece (Fig. for #19). The total separation
of the lenses is 22 cm + 2 cm = 24 cm.
- If the object's size is y, the real image formed at F2
is y’ = y(si1/so1)
= y(22 cm/2.2 cm) = 10y. Since the eyepiece is adjusted
for minimum eyestrain, its magnifying power is given by
25/f = 25/2 = 12.5. The over-all magnifying power of the
instrument is the product of the two magnifications = M
= (10)(12.5) = 125.
|
|
|
20.
|
First find the two focal lengths in meters.
fo = 40 cm = 0.40 m 1/fe = 50 D = 50 m-1.
fe = 1/50m = 0.02 m.
M = fo/fe = 0.40/0.02 = 20.
This is a low-power telescope, which is desirable when a large
area of the sky is to be scanned.
|
|
|
21.
|
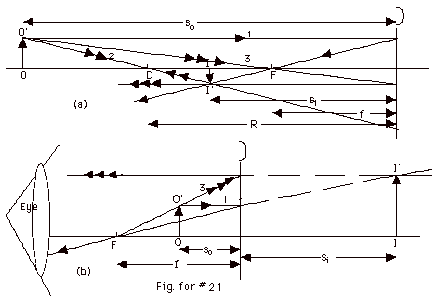
- 1/si = 1/f - 1/so = 1/10cm - 1/30cm
= (3 - 1)/30cm.
si = 15 cm
m = - si/so = -15/30 = -1/2.
Image is real, inverted, and diminished.
- 1/si = 1/f - 1/so = 1/10cm - 1/5cm
= (1 - 2)/10cm.
si = -10 cm.
m = - si/so = - (-10cm)/5cm=
+ 2.
Image is virtual, erect, and enlarged.
In the ray diagrams for the concave mirror, (1) a ray drawn
parallel to the principal axis is reflected back through
the focal point, (2) a ray drawn through the center of curvature
hits the mirror normally (angle of incidence = 0) and is
reflected back on itself (angle of reflection = 0), and
(3) a ray drawn through the focal point is reflected back
parallel to the principal axis.
|
|
|
22.
|
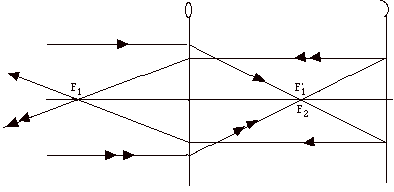
In the figure above, parallel rays incident on the converging
lens pass through its focal point F’1 and the
focal point F2 of the concave mirror, hit the mirror,
and are reflected back parallel to the principal axis. After
returning through the converging lens they pass through its
focal point at F1.
|
|
|
23.
|
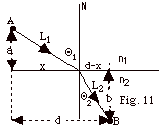
From the geometry of Fig. 11 above,
L1 + L2 = (a2
+ x2)1/2 + [b2 + (d - x)2]1/2
t = L1/v1 + L2/v2
t = (a2 + x2)1/2/(c/n1)
+ [b2 + (d - x)2]1/2/(c/n2)
dt/dx = n1x/c(a2 + x2)1/2
- n2(d - x)/c[b2 + (d -x)2]1/2
For a minimum, dt/dx = 0 or
n1x/(a2 + x2)1/2
= n2(d - x)/[b2 + (d -x)2]1/2
n1 sin Θ1
= n2 sin Θ2
|
|
|
24.
|
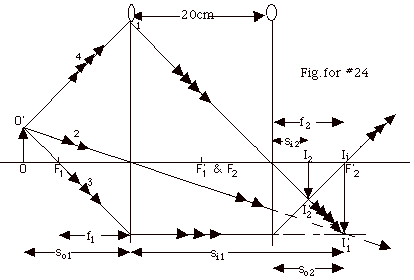
For the first image, 1/si1 = 1/f1 - 1/so1
= 1/10cm - 1/15cm = (3 - 2)/30cm
= 1/30cm. si1 = 30 cm. With a distance
of 30 cm from the first lens and a lens separation of 20 cm,
the image of the first lens (had the second lens not been there)
would be formed 10 cm to the right of the second lens.
We say this object distance for the second lens is virtual and
designate this by taking so2 = -10cm. Then
1/si2 = 1/f2 - 1/so2 = 1/10cm
- (-1/10cm) = 2/10 cm, or si2 = 5 cm
to the right of the second lens. For the first lens, m1
= - si1/so1 = - 30/15 =
- 2. For the second lens, m2 = - si2/so2
= - 5/(-10) = +1/2. Total magnification = m1m2
=(-2)(1/2) = - 1.
In Fig. for #24 above, ray 2 is drawn from the top of the object
at O’ through the center of the lens. Ray 3 is drawn through
the focal point of the first lens F1 and is refracted
through the first lens parallel to the principal axis. If the
second lens had not been there, these two rays would meet at
the top of the first image I’1. Any other ray
that starts from O’ will also be refracted through the
first lens to arrive at I’1. Ray 4 in Fig.
for #24 that passes through the center of the second lens will
continue there even with the second lens. (You draw it backwards.
Starting at I’1 draw a line that passes through
the center of the second lens until it hits the axis of the
first lens. Then draw a line from O’ to the point where
it hits the axis of the first lens.) Ray 3 that arrives at the
second lens parallel to the principal axis will be refracted
through the focal point of the second lens. Rays three and four
meet at the top of the second image at I’2.
Thus the second image appears as shown in Fig. for #24 as
I2I’2. The final image is
real (note si2 > 0), inverted (first lens inverted
the image, but second lens did not invert that image), so the
final image is the inverted and the same size as the original
object (m1m2) = - 1.
|
|
|
25.
|
1/fred = (n – 1)(1/R1
+ 1/R2) = (1.51 – 1)(1/38 cm + 1/38 cm) = 0.0268
cm-1
1/f – 1/so = 0.0268 cm-1 –
1/95 cm = 1/si = 0.0163 cm-1. si
= 61.3 cm.
1/fblue = (n – 1)(1/R1 + 1/R2)
= (1.54 – 1)(1/38 cm + 1/38 cm) = 0.0284 cm-1
1/f – 1/so = 0.0284 cm-1 –
1/95 cm = 1/si = 0.0179 cm-1. si
= 55.9 cm.
You can buy a camera with an acromatic lens that corrects for
the variation in the index of refraction with color. This problem
shows the cost may be worth it.
|
|
|
26.
|
Since we want the farthest point for
the eye to be at infinity, we take so equal to
∞. Because we need these rays to appear to come
from 4.0 m, the far point, we take si to be - 4.0
m. The image distance is negative because the rays do not
really meet there, but appear to the eye to come from there.
1/so + 1/si = 1/∞ + -1/4.0m =
1/f. f = - 4.0m. Diopters = 1/f = - 0.25
D.
|
|
|
27.
|
Now we want the rays to appear to come
from 1.25 m when we place an object at the accepted near point
of 0.25 m.
so = 0.25 m and the virtual image position si
= - 1.25m.
1/so + 1/si = 1/0.25m + -1/1.25m = 1/f.
f = +0.312 m. Diopters = +3.2 m-1 = +
3.2 D.
|
|