|
Answers - Physical Optics
|
|
|
1.
|
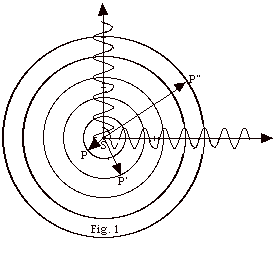
- The concentric circles are cross-sections of spherical
wave fronts that pass through the crests of the waves. The
distance between crests equals one wavelength λ.
- The distance SP is from one crest to another or λ.
- The distance SP’ is 2 λ.
- The distance SP” is 5 λ.
- The distance between a crest and a trough is λ/2.
The wavefronts through troughs would be spheres halfway
between the spheres that represent the wavefronts through
the crests. In the figure you would represent their cross-sections
with circles.
|
|
|
2.
|
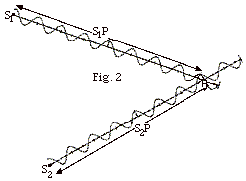
- Counting the number of crests from S1 to P
you find S1P = 8 λ.
- Counting the number of crests from S2P = 7 λ.
- The path difference S1P - S2P =
λ.
- For a path difference of an integral number of wavelengths,
there will be constructive interference.
|
|
|
3.
|
Frequency f is the number
of oscillations of the source of the wave per second, wavelength
λ is the distance traveled
by the wave in one complete oscillation of the source and velocity
is the distance traveled by the wave in one second.
| number
of oscillations |
x |
distance
traveled |
= |
distance
traveled |
| second |
oscillation |
second |
| f |
x |
λ |
= |
v |
|
|
|
4.
|
For the first minimum, the path difference
= λ/2 = (10 - 8)ft = 2
ft and the wavelength λ=
4 ft. The speed of sound v = λf
= (4 ft)(275 s-1) = 11 x 102 ft/s.
|
|
|
5.
|
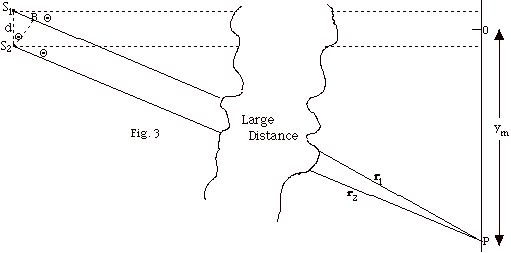
- For a maximum the path difference equals an integral number
of wavelengths, λ, 2 λ,
3 λ, . . . S1P
= m λ, where m = 0, 1,
2, 3, . . . .
- In triangle BS1S2 of Fig. 3 above,
sin Θ = S1B/d
= m λ/d,
or m λ = d sin Θ
for a maximum.
- For a minimum the path difference equals λ/2,
3 λ/2, 5 λ/2,
. . .
S1P = (m + 1/2) λ,
where m = 0, 1, 2, 3, . . . .
In triangle BS1S2, sin Θ
= S1B/a = (m + 1/2) λ/d,
or m(1 + 1/2) λ = d sin
Θ for a minimum.
|
|
|
6.
|
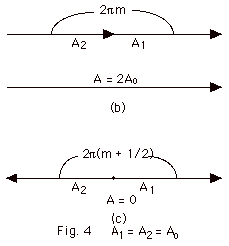
For Fig. 4b above,
- The resultant amplitude A = A1 + A2
= 2Ao, where A1 = A2
= Ao.
- The phase difference = 0, 2 π,
3 π, . . . or ΔΦ
= 2m π,
m = 0, 1, 2, 3, . . .
For Fig. 4c above,
- The resultant amplitude A = A1 - A2
= 0, where A1 = A2 = Ao.
- The phase difference = π,
3 π, 5 π,
. . . or ΔΦ =
2 π(m + 1/2),
m = 0, 1, 2, 3, . . .
|
|
|
7.
|
ΔΦ =
2 π(r1 - r2)/ λ
= 2 π (path difference)/ λ.
- For constructive interference, ΔΦ=
2 πm = 2 π
(r1 - r2)/ λ
or path difference = (r1 - r2) = m λ,
m = 0, 1, 2, 3, . . .
- For destructive interference, ΔΦ=
2 π (1 + 1/2)m = 2 π
(r1 - r2)/ λ
or path difference = (r1 - r2) = m(1
+ 1/2) λ, m = 0,
1, 2, 3, . . .
|
|
|
8.
|
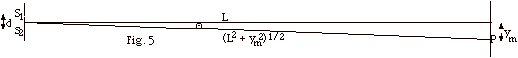
In Fig. 5 above, sin Θ=
ym/(L2 + ym2)1/2
≈ ym/L = tan Θfor small Θ.
- For constructive interference sin Θ
= m λ/d ≈ ym/L.
Dropping the approximate sign, ym = m λL/d.
- Δy = ym+1
- ym = (m + 1) λL/d
- m λL/a = λL/d.
- For destructive interference sin Θ
= (m + 1/2) λ/d ≈
ym/L.
- ym = (m + 1/2) λL/d.
- (b) Δy = ym+1
- ym = (m + 1 + 1/2) λL/d
- (m + 1/2) λL/d
= λL/d.
|
|
|
9.
|
From Fig. 4a below, Ax
= A2 + A1 cos ΔΦ.
Ay = A1 sin ΔΦ.
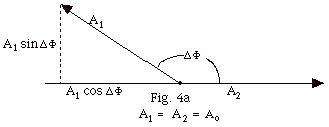
- A2 = [(A2 + A1 cos ΔΦ)2
+ (A1 sin ΔΦ)2]
A2 = A22 + 2A2A1
cos ΔΦ + A12
cos2 ΔΦ+
A12 sin2 ΔΦ
A2 = A22 + 2A2A1
cos ΔΦ + A12
= 2Ao2(1 + cos ΔΦ)
A2 = 2Ao2(2 cos2 ΔΦ/2)
A2 = 4Ao2 cos2 ΔΦ/2.
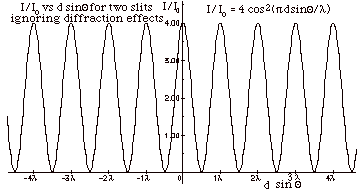
- I/Io = (A/Ao)2 = 4 cos2
ΔΦ/2. I
= Io cos2 ΔΦ/2,
where ΔΦ/2= πd
sin Θ/ λ.
|
|
|
10.
|
- For direction (a) the waves from each antenna travel the
same distance to a distant point. The path difference and
the phase difference are zero.
A = 3Ao and I = 9Io. Fig.
for 10(a)
- For direction (b) the path difference between the wave
from antenna 2 and 3 is 90 m sin 30o = 45 m =
λ/4.
ΔΦ = 2 π(path
difference)/ λ= 2 π( λ/4)/ λ=
π/2. The path difference
between antenna 1 and 3 is 180 m sin 30o = 90
m = λ/2.
ΔΦ= π.
A = A2 = Ao. I = Io. Fig.
for 10(b)
- For direction (c), the path difference between the wave
from antenna 2 and 3 is 90 m = λ/2.
ΔΦ =2 π(path
difference)/ λ= 2 π( λ/2)/ λ=
π. The path difference
between antenna 1 and 3 is 180 m = λ.
ΔΦ= 2 π.
A = A3 - A2 + A1 =
Ao. I = Io. Fig.
for 10(c)
|
|
|
11.
|
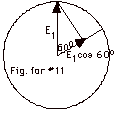
When the unpolarized light goes through the first polarizer,
its irradiance drops by a factor of two. With Io
= 1000 W/m2, I1 = 500 W/m2.
When it passes through the second polaroid, I2
= I1 cos2 60o = 500 W/m2
(1/4) = 125 W/m2.
|
|
|
12.
|
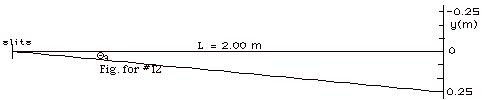
- For constructive interference m λ
= d sin Θm,
where m is an integer
= 0, 1, 2, 3 . . . ., λ
is the wavelength of the light, d is the distance between
the sources or slits, and Θm
is the angle for the mth maximum. Thus sin Θ3
= m λ/d = 3(656 x 10-9
m)/(1.57 x 10-5 m) = 0.125. Θ3 = 7.2o.
- For small angles sin Θ
≈ tan Θ ≈
y/L.
Thus y3 ≈ LΘ3
= 2.00 m(0.125) = 0.25 m.
|
|
|
13.
|
In general, λo
= c/f, where f is the frequency of the light and λo
and c are the wavelength and the speed of light in a
vacuum or approximately in air, respectively. The frequency
is a property of the source and not of the medium. When a
wave enters a different medium, its wavelength and speed change,
but its frequency remains the same. For a film with index
of refraction n, the wavelength λn
= v/f = (c/n)/f = (c/f)(1/n) = λo/n,
since n = c/v or
v = c/n.
|
|
|
14.
|
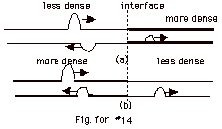
When a pulse goes from a less to denser
medium, the reflected wave experiences a 180o or
π phase change. When it
goes from a more to less dense medium, there is no change
of phase for the reflected wave. (Fig. for #14). From a crest
to a trough is a distance of λ/2.
A change of phase of 180o or π
is equivalent to a path difference of λ/2.
Notice that there is never a change of phase for the transmitted
ray at an interface. The speed of light is greatest in a vacuum
or approximately air with index of refraction n = 1 = c/v.
The higher the index of refraction, the smaller the speed
in the medium. When light goes from medium 1 to medium 2,
the reflected ray will experience a phase change of π if
n2 > n1. There will be no phase
change if n2 < n1.
|
|
|
15.
|
ym = m λL/d
or
m = ymd/L λ=
(1.50 x 10-3 m)(1.00 x 10-3 m)/(1.00
m)(500 x 10-9 m) = 3.
|
|
|
16.
|
Δy
= λL/d.
The distance between maxima Δy
is directly proportional to the wavelength λ
and inversely proportional to the distance d between the slits.
If the wavelength is halved, the distance between maxima is
halved. If the distance between the slits is doubled, the
distance between maxima is halved. The combination means the
distance between maxima is reduced by a factor of four.
Δy’ = Δy/4.
|
|
|
17.
|
The distance between maxima Δy
is directly proportional to the wavelength λ.
The wavelength of light in water λn
of index of refraction n equals the wavelength λo
in air or a vacuum divided by n. Since n > 1,
λn is less
than λo and
the distance between maxima is smaller when the interference
pattern is observed under water.
|
|
|
18.
|

The distance from A to B is 5.00000 cm. The path from A to
the mirror to B is 1.60010 cm + 3.40020 cm = 5.00030 cm.
The difference in path is (5.00030 cm + λ/2)
- 5.00000 cm = 0.00030 cm + λ/2.
The addition of λ/2 to
the path from A to the mirror to B occurs because of the change
of phase of π when the
light is reflected from the mirror. For a minimum at B, the
path difference = 0.00030 cm + λ/2
= (m + 1/2) λ or
0.00030 cm = m λ.
For m = 1, λ= 0.00030
cm = 30 x 10-7 m.
For m = 2, λ= 0.00015
cm = 15 x 10-7 m.
|
|
|
19.
|
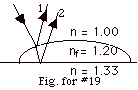
When the light goes from air to oil, the reflected wave 1 experiences
a change of phase of π.
The light that enters the oil is partly reflected at the oil-water
interface. Again at this interface, the reflected wave experiences
a change of phase of π,
but it has no change in phase as it goes from the oil back into
the air as the transmitted ray 2. The change of phase are additive.
For both reflections, the total change of phase is π
+ π = 2 π,
which is equivalent to no change in phase.
There is, however a path difference as the ray travels down
and back up in the oil. For almost normal incidence we say the
thickness of the oil there is d and the path difference
2d = m λf,
m = 0, 1, 2, 3 . . . for constructive interference,
or
2d = (m + 1/2) λf,
m = 0, 1, 2, 3 . . . for destructive interference,
where λf is the
wavelength of the light in the film.
- For the outer or thinnest regions of the drop, d approaches
zero and there is no overall phase change or thickness so
there is a maximum intensity of light.
- For a maximum 2d = m λf
= m λo/nf.
Thus possible d's are do = 0, d1=
1(580 nm)/2(1.20) = 242 nm.
d2 = 2(580 nm)/(2)(1.20)= 484 nm, etc.
|
|
|
20.
|
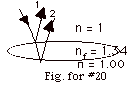
Now there is a change of phase at the interface between the
air and the soap film so that ray 1 is reflected with a change
of phase of π. But
there is no change of phase at the second film-air interface
because now the ray is going from nf to n, where
nf > n. This is similar to adding (or
subtracting) a path difference of λf/2.
For constructive interference, the path difference = 2d =
(m + 1/2) λf
or
d = (m + 1/2) λo/2nf
.
- For m = 2, a maximum occurs for d = (2 + 1/2)(580 nm)/2(1.34)
= 541 nm.
A minimum occurs for a path difference = 2d + λf/2
= (m + 1/2) λf,
or
2d = m λf,
which would have been the condition for a maximum had there
been no change in phase of the reflected ray.
Now for a minimum, d = m λf/2
= m λo/2nf.
- For m = 2, a minimum occurs for d = 2(580 nm)/2(1.34)
= 433 nm.
|
|
|
21.
|
The sound is diffracted as it goes through
the "slit" of the door with the longer wavelengths
"bent" the most around the "slit". These
wavelengths will be accentuated. The longer wavelengths correspond
to lower-frequency notes.
|
|
|
22.
|
The wavelengths of sound are much greater
than the wavelengths of visible light. Thus it is much easier
to detect interference and diffraction properties of sound
waves.
|
|
|
23.
|
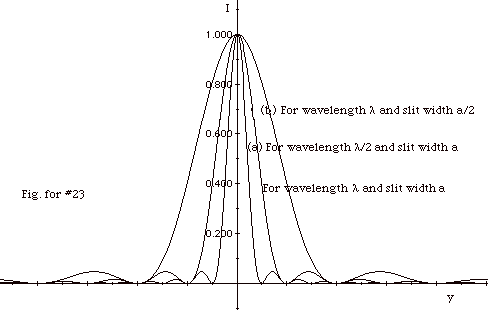
For small angles, the position of the minima ym’
is directly proportional to the wavelength λ and
inversely proportional to the slit width a.
- When the wavelength is halved, but slit width remains
the same, the first minimum is closer to the central maximum
and the distance between minima is smaller (Fig. for #23a).
y1 for (a) is half the original y1
and the distance between minima Δy
for (a) is half the original Δy.
- When the slit width is halved, but wavelength remains
the same, the first minimum is further from the central
maximum and the distance between minima is greater (Fig.
for #23b).
y1 for (b) is twice the original y1
and the distance between minima Δy
for (b) is twice the original Δy.
|
|
|
24.
|
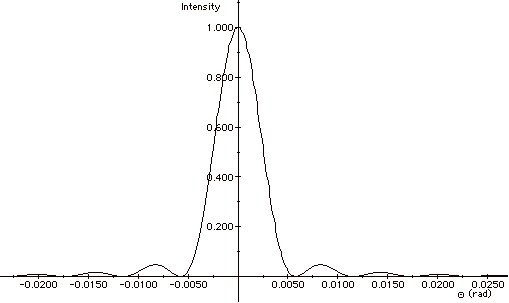
For a minimum sin Θm’
= m’ λ/a.
For m’ = 1, the width of the slit a = 1.00 x 10-4
m and
λ = 580 x 10-9 m,
sin Θ1 = 1(580
x 10-9 m)/10-4 m = 0.00580 ≈ Θ1.
The width of the central maximum ≈ 2LΘ1
= 2(2.0m)(0.0058) = 2.32 x 10-2 m. Plot of the intensity
as a function of angle is shown in the figure above.
|
|
|
25.
|
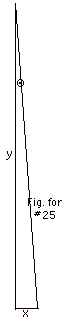
The angular limit of the resolution for the terrestrial telescope
=
Θa = 1.22 λ/D
= (1.22)(550 x 10-9 m)/(6.5 x 10-2 m)
= 1.03 x 10-5.
In Fig. for #25 above (not to scale), tan Θ=
x/y = x/1000 m,
where x equals the minimum distance of separation and y equals
the distance from the objects.
For small angles the tangent of the angle is approximately
equal to the angle in radians.
1.03 x 10-5 = x/ 1000 m or
x = (103 m)(1.03 x 10-5) = 1.03 x
10-2 m = 1.03 cm.
|
|
|
26.
|
In general for a maximum, sin Θm
= m λ/d.
In this problem, d = 1 divided by the number of lines
per meter
= 1/(2.00 x 105/m) = 5 x 10-6 m.
For λ= 653.4 x 10-9
m and m = 1,
sin Θ1 = (1)(653.4
x 10-9 m)/(5 x 10-6 m) = 0.131 and Θ1
= 7.51o.
For λ= 653.4 x 10-9
m and m = 3,
sin Θ1 = (3)(653.4
x 10-9 m)/(5 x 10-6 m) = 0.393 and Θ3
= 23.1o.
For λ= 580.8 x 10-9
m and m = 1,
sin Θ1 = (1)(580.8
x 10-9 m)/(5 x 10-6 m) = 0.116 and Θ1
= 6.67o.
For λ= 580.8 x 10-6
m and m = 3,
sin Θ1 = (3)(580.8
x 10-9 m)/(5 x 10-6 m) = 0.348 and Θ3
= 20.4o.
For the first order, the angular separation for the α
and β lines is
(7.51 - 6.67)o = 0.84o.
In the third order, the angular separation for the α
and β lines is
(23.1 - 20.4)o = 2.7o.
You get greater angular separation of the lines in the higher
orders.
|
|
|
27.
|
- In general for a maximum, sin Θm
= m λ/d.
For two lines that are adjacent, the m's differ
by 1.
Let m be the order for sin Θ
= 0.2 and m + 1 the order for sin Θ=
0.3.
Then,
0.2d = m λ (Equation
1)
0.3d = (m + 1) λ (Equation
2)
Eq. 2 - Eq. 1 gives
0.1d = λ
or
d = λ/0.1 = 600 x
10-9 m/0.1 = 6.0 x 10-6 m.
- Minima of diffraction patterns occur for a sin Θm’
= m’ λ, where a
is the slit width. Since the fourth order interference maxima
is missing it must fall at one of these angles. If a is
the smallest slit width for which this order is missing,
the order must correspond to m’ = 1 and the angle
is given by sin Θ1
= (1) λ/a.
This angle is also given for m = 4 for the interference
pattern by sin Θ4
= 4 λ/d.
Thus λ/a = 4 λ/d
or
a = d/4 = (6 x 10-6 m)/4 = 1.5 x 10-6 m.
- First set Θ = 90o
and find the largest value of m for which m λ
< d sin Θ. This is
the highest order that is diffracted toward the screen.
The condition is the same as m λ
< d or m < d/ λ
= 6 x 10-6 m/600 x 10-9 m = 10. The
highest order seen is m = 9. The fourth and
the eight order are missing so the observable orders are
m = 0, 1, 2, 3, 5, 6, 7, and 9.
- The intensity at the screen is given by I = Io
(cos2β)
(sin α/α)2
where α = ( πa/ λ)sin
Θ and β
= ( πd/ λ)sin
Θ, and Io
is the intensity of the central maximum. For the third
bright line d sin Θ
= 3 λ, so β
= 3 π and
cos2 β =
1.
α = 3πα/d
= 3 π/4. (sin
α/α)2
= [(sin 3 π/4)/3 π/4]2
= 0.090.
I = 0.090Io.
|
|
|
28.
|
I = Io cos2
Θ.
I/Io = 1/2 = cos2 Θ.
cos Θ
= (1/2)1/2.
cos-1 (1/2)1/2 = 45o
|
|
|
29.
|
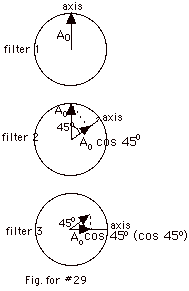 |
After going through
the first filter, the light has an amplitude of Ao
and its polarization is vertical. When this light goes
through the second filter that is at an angle of 45o
with the axis of the first filter, the amplitude
is the projection of Ao on the new axis which
is Ao cos 45o. The third
filter is at an angle of 90o with the first
filter, but at an angle of 45o with the second
filter. After passing through the third filter, the amplitude
is
Ao cos 45o(cos 45o)
=
Ao cos2 45o =
Ao [(1/2)1/2]2 =
Ao/2.
The intensity is proportional to the amplitude square.
I/Io = (Ao/2)2/Ao
or
I = Io/4 = 25% Io. |
|
|
|
30.
|
Let n1 = 1 and
n2 = 2.42.
tan Θ1 = 2.42.
Θ1
= 67.6o.
|
|
|
31.
|
Since the polarizing angle found in #30
was 67.6o it can't be diamond.
tan 62.5o = 1.92, which is the index of refraction
of zircon.
|
|
|