|
|
- Descriptive Terms
- Period T equals the time for one complete oscillation of
the source that produces the wave.
- Frequency f equals the number of oscillations per
second.
- Wavelength l equals
the distance moved by the wave in one period or in one oscillation.
(distance/oscillation) x ( number of oscillations/s) = (distance/s)
- Velocity v equals distance moved by the wave per second.
- Equation of motion for a traveling wave
- The displacement y of a point on a traveling wave depends
on the distance x from the source and the time t. y
is a function of x and t.
- Each point on the wave vibrates with simple harmonic motion
of the same amplitude and frequency, but there is a phase
difference between the motion of a point at x and a point
at x’ ≠ x if x’ ≠
(x ± nl)
where n = 0, 1, 2, . . . . Points separated by l
vibrate in phase; points separated by l/2
vibrate 1800 out of phase.
- y(x,t) = A sin (2px/l
± 2pt/T), where
the - sign is used for a wave traveling to the right and the
+ sign for a wave traveling to the left. If the wave is traveling
to the right, you want the function at x > 0 to be equal
to the function at x = 0 and t = 0. To insure this you subtract
vt and then f(x - vt) = f(0). If the wave is traveling to
the left then the x is getting smaller and you have to add
vt.
- Letting k = 2p/l
and w = 2p/T
= 2pf, we may write y(x,t)
= A sin (kx ± wt).
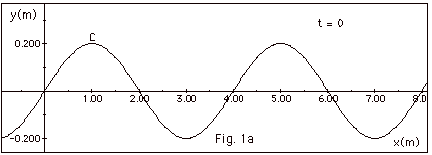
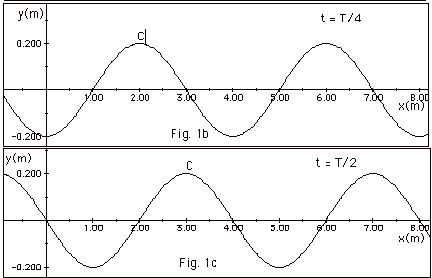
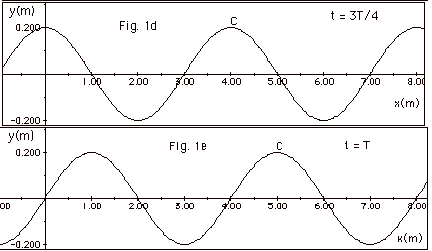
- Fig. 1a below shows a travelling wave with
l = 4 m at t = 0. A crest C appears at x = 1 m. The
following figures show the shape of the wave as it travels
to the right. Since a wave travels one-wavelength l
in one period T, it travels l/4
in time T/4. In Fig. 1b below, at time t = T/4 the crest C
has moved from x = 1.0 m to x = 2.0 m a distance of 1 m =
l/4. At t = T/2,
t = 3T/4, and T, the crest has moved l/2,
3l/4, and l,
respectively.
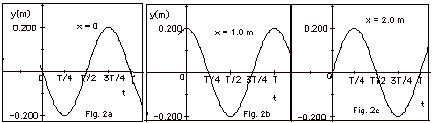
- In Fig. 2 below, I have plotted y as a function of time
for three values of x. If you look back at Fig. 1 above and
concentrate on the point at x = 0 and find the value of y
for t = 0, T/4, T/2, 3T/4, and T, you will see that a plot
of y as a function of t looks like Fig. 2a below. Now concentrate
on the point at x = 1.0 m and you will find that a plot of
y as a function of t looks like Fig. 2b below. A plot of y
as a function of t for x = 2.0 m is shown in Fig. 2c below.
Notice that all points on the wave vibrate up and down with
the same amplitude and frequency, but they are not in phase.
If you look at Fig. 2a and Fig. 2c below, you find the particles
are 180o out of phase.
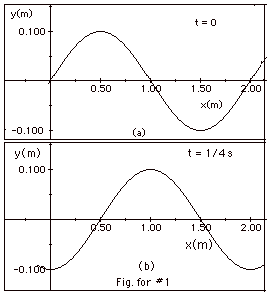
- Sample problem 1. For the wave shown in Fig. for #1a below,
the displacement of the wave as a function of x is shown for
t = 0. In Fig. for #1b below, y is shown as a function of
x for t = 1/4 s. This is the first time the wave looks this
way after t = 0. Find (a) the amplitude of the wave, (b) the
wavelength of the wave, (c) the period of the wave, (d) the
frequency of the wave, (e) the velocity of the wave, and (f)
the direction in which the wave is moving. Explain your answer
to (f).
- Sample Problem 2. Given y(x,t) = 4 cm sin (p
m-1 x - 4p s-1
t) find (a) the amplitude , (b) the wavelength, (c)
the period, (d) the frequency (e) the velocity of the wave
and (f) the direction in which it is moving.
- Sample Problems in 104
Problem Set for Wave Motion: 1-4, 7-10.
- Standing Wave
- A standing wave is formed by combining a wave to the right
and to the left. For a standing wave,
y(x,t) = y1(x,t) + y2(x,t)
y(x,t) = A sin (2px/l
- 2pft) + A sin
(2px/l
+ 2pft)
= A[sin 2px/l
cos 2pft - cos 2px/l
sin 2pft}
+
A[sin 2px/l
cos 2pft + cos 2px/l
sin 2pft}
= 2A sin
2px/l
cos 2pft = (2A sin 2px/l)
cos 2pft
- This reminds us of the equation for simple harmonic motion:
y(x,t) = (Amplitude) cos 2pft
or y(x,t) = (Amplitude) cos wt
- For a standing wave, all points on the wave do not have
the same amplitude.
- In fact, when sin 2px/l
= 0, the displacement of the rope at those points never
have any displacement. These points are called nodal
points and occur when 2px/l
= 0, p, 2p,
3p, 4p,
etc. A neat way to write this is to say you get a nodal
point when 2px/l
= mp, where m = 0,
1, 2, 3, 4,. . . or x = mpl/2p
or x = ml/2.
(A historical note here. This was the first time that
a quantity took on integral values or discrete values.
In other words, the values were not continuous. This is
a foundation of quantum mechanics.) The distance between
nodal points = Dx
= (m + 1)l/2 - ml/2
= l/2.
- Positions of maxima with amplitude 2A, where A is the
amplitude of a single wave, are called antinodes. They
occur for sin 2px/l
= 1 or 2px/l
= (m + 1/2)l or x
= (m + 1/2)l/2. The
distance between antinodes is again l/2.
- All points, except the nodal points, on the standing
wave vibrate with simple harmonic motion, but the amplitudes
vary from zero at a nodal point to a maximum at an antinodal
point. The entire string on which a standing wave exists
has zero displacement twice each period.
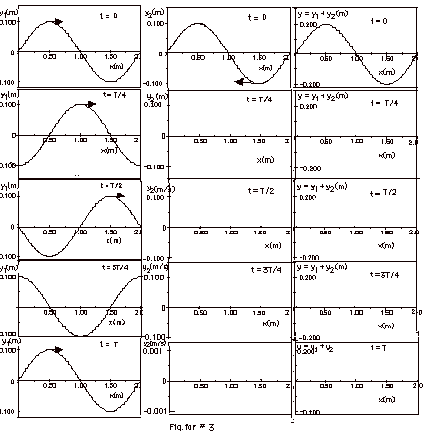
- Sample Problem 3. Below, I have drawn y1(x,t),
y2(x,t), and y(x,t) = y1(x,t) + y2(x,t)
for t = 0. You find y(x,t) by adding the displacements of
y1(x,t) and y2(x,t) for a given time
t. I have also drawn y1(x,t) for t = T/4, t = T/2,
t = 3T/4, and T. Notice that the crest at x = 0.50 m for y1(x,t)
at t = 0 moves to x = 1.0 m at t = T/4. In other words, the
wave moves l/4 in time
T/4. You are to complete the figure by drawing y2(x,t)
and y(x,t) for t = T/4, t = T/2, and T = T. How do the y(x,t)
compare at time t = 0 and t = T? Is this what you would have
expected? What are the distances between nodes in the y vs
x curves? What are the distances between antinodes in the
y vs x curves?
- Sample Problems in 104
Problem Set for Wave Motion: 11,
and 21-24.
- Solution to Sample Problems
- From Fig. for #1 below, (a) the amplitude of the wave is
0.100 m. (b) the wavelength = 2.00 m. (c) In Fig. b, the crest
has moved 0.50 m to the right in 1/4 s. Since 0.50 m = l/4,
the time elapsed = T/4. T = 1.0 s. (d) The frequency f = 1/T
= 1.0 s-1. (e) lf
= v = (2.00 m)(1 s-1) = 200 cm/s.
(f) Since the crest moves to the right, the wave is moving
to the right.

- Given
y(x,t)
= 4 cm sin (p m-1
x - 4p s-1
t)
Compare with
y(x,t)
= A sin (2px/ l
± 2pt/T)
(a) A = 4 cm, (b) 2p/ l
= p m-1
or l = 2 m, (c) 2p/T
= 4p s-1 or
T = 0.5 s
(d) f = 1/T = 2 s-1 s, (e) v = lf
= (2 m)(2 s-1) = 4 m/s (f) The wave travels to
the left because f(x,t) = f(x –vt)
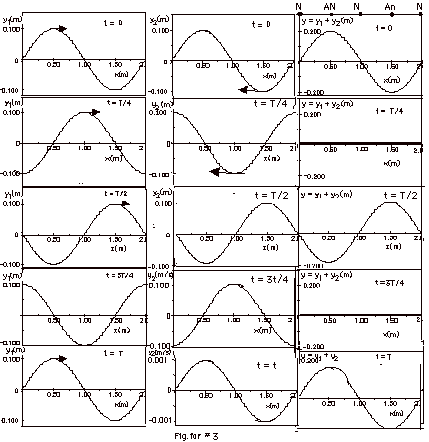
- As illustrated in the figure below, equation of wave to
the right is y1(x,t) = 0.10 m sin (p
m-1x - 2pft).
The equation of the wave to the left is y2(x,t)
= 0.10 m sin (p m-1x
+ 2pft). The equation
of the standing wave is y(x,t) = 0.20 m sin p
m-1x cos 2pft.
Nodal points are 1.00 m apart = l/2 = distance between antinodal
points. After one period T, the waves look the same as they
did for t = 0.
|
|