Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 106

Outline - Circuits
  1. Electric Circuits - Definition of terms

    1. Electric current  I equals the rate of flow of current.
      For constant current  I = q/t.  For a variable current  I = dq/dt.




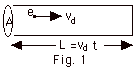
    2. In Fig. 1 above, an electron moves in a conductor with the equivalent of a constant drift velocity vd in a constant electric field E. In reality the electron experiences a series of accelerations in the electric field after collisions with nucleus and inner electrons of the atoms that make up the material. Let n = the number of electrons/volume, e the charge on the electron, A the cross-sectional area of the conductor, and L its length = vdt,  where t is the time for the electron to move the length of the conductor. The net charge in motion is then q = neAvdt  and the current I = q/t = neAvd.

    3. Sample problem in 106 Problem Set for Circuits: 1.


  2. Resistances

    1. The resistance R of a conductor is directly proportional to its length L, inversely proportional to its cross-sectional area A, and depends on the material's resistively r.   R = rL/A.

    2. Ohm's Law. The potential difference Vab  across a resistance R from a to b with a current  I  from a to b is given by Ohm's Law, an Empirical law,
      Vab = IR.

    3. Combinations of Resistors

      1. Resistors in Series

        1. The current  I is the same in each resistor

        2. The potential difference across all of the resistors equals the sum of the individual potential differences:
          Vab = Vac + Vcd + Vdb

        3. Req = Vab/I = Vac/I + Vcd/I + Vdb/I = R1 + R2 + R3
           (Fig. 2a below)



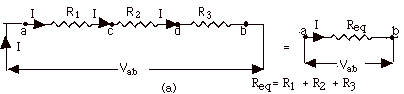
      2. Resistors in Parallel

        1. The potential difference Vab across each of the resistors is the same.

        2. The total current I equals the sum of the currents in each of the resistors:   I = I1 + I2 + I3

        3. I/Vab = I1/Vab + I2/Vab + I3/Vab

        4. 1/Req = 1/R1 + 1/R2 + 1/R3  (Fig. 2b below)




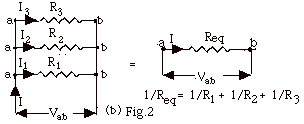
    4. Sample problems in 106 Problem Set for Circuits: 2, 3, 7.


  3. Power

    1. Power = P = (Ua - Ub)/t = q(Va - Vb )/t = (q/t)(Va - Vb ) = IVab
       The above statement is always true.

    2. If the circuit element between a and b is an Ohmic resistor for which
      Vab = IR,  then P = I(Vab ) can be written as P = I(IR) = I2R  or
      P = (I)Vab  can be written as P = (Vab/R)Vab = (Vab)2/R.

    3. Sample problem in 106 Problem Set for Circuits: 4.


  4. Electromotive force e

    1. The electromotive force e = energy/charge = U/q  or
      qe = U  and power = P = U/t = (q/t)e = Ie.



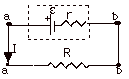
    2. For the circuit of Fig. 3 above, r is the internal resistance of the battery. For this circuit:
      Power in = Power out
      Chemical power to electrical power = electrical power to heat
      Ie = I2R + I2r        (Equation 1)

      1. From Eq. 1,

        1. I = e/(R + r)

        2. e - Ir = IR = Vab

        3. The terminal voltage across a battery Vab = e-Ir

      2. Sample problems in 106 Problem Set for Circuits: 5, 8.


  5. Kirchhoff's Rules

    1. Junction rule. The sum of the currents entering any junction equals the sum of the currents leaving that junction. This is just a statement of conservation of charge.

    2. Loop rule. The sum of the potential differences across each element around any closed circuit loop is zero. This is just a statement of conservation of energy.

      1. If you go from the minus to the plus side of the battery, chemical energy is being changed into electrical energy and you are picking up energy, thus the sign is plus. If you go from the plus side of the battery to the minus sign, the sign is negative.

      2. If go around the loop in the same direction as the current, electrical energy is being converted to heat and you are losing energy so this IR is negative. If you go around the loop opposite to the direction of the current, you are going from a lower potential to a higher potential so this IR is positive.

      3. General comment. Once you choose directions of currents, and going around the loop clockwise or counterclockwise, stay with it. You may reverse the direction of going around the loop for a second loop, but don't change the directions of the currents.

    3. Sample problem in 106 Problem Set for Circuits:  9.



  6. RC-Circuits



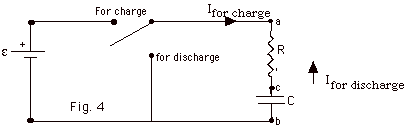
    1. The potential difference across an Ohmic resistor = IR
      and across a capacitor = q/C

    2. When the switch S is thrown up for the charging position

      1. Using the loop rule, we find
        e = IR + q/C.
        Since I = dq/dt, we may write this as
        e = dq/dt R + q/C            (Equation 2)
        Arithmetic gives us
        (dq/dt)RC = -(q - eC)         (Equation 3)
        Separating the variables:
        dq/(q - eC) = -1/RC dt             (Equation 4)
        Integrating both sides:

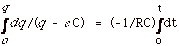
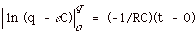           or
        ln [(q- eC)/-eC} = -t/RC                         (Equation 5)
        Taking the antilog of both sides of Eq. 5:
        (q- eC)/-eC = e-t/RC
        q - eC = -eC(e-t/RC )   or finally
        q(t) = eC(1 - e-t/RC )                   (Equation 6)
      2. The potential difference across the capacitor for charging the capacitor Vcb  sometimes called
        VC = q/C = e(1 - e-t/RC ).      (Equation 7)
      3. The current  I = dq/dt = e/R( e-t/RC )                   (Equation 8)

      4. The potential difference across the resistor for charging the capacitor Vac  sometimes called
        VR = IR = e( e-t/RC )              (Equation 9)
      5. For Figures 4 (above) and 5 (below),  I have chosen e = 1.0V,
        R = 106 W = 106 V/A,  and C = 5 x 10-6 F = 5 x 10-6 C/V.  The time constant = RC =106 V/A x 5 x 10-6 C/V = 5 C/A = 5 C/(C/s) = 5 s.

        For build up of charge,  VC(t) = e(1 - e-t/RC).  When t = RC = 5 s,
        VC(RC) = 1.0 V(1 - e-RC/RC ) = 1.0 V( 1 - e-1) = 1.0 V(0.632) = 0.632 V, as shown below.





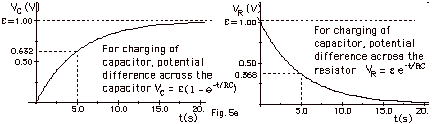
        For build up of charge,  VR(t) = ee-t/RC.  When t = RC = 5 s,
        VC(RC) = 1.0 V( e-RC/RC ) = 1.0 V(e-1) = 1.0 V(0.368) = 0.368 V, as shown above.

    3. When the switch is thrown down, the battery is no longer in the circuit and the capacitor discharges.

      1. Vab = 0 = IR + q/C = dq/dt R + q/C             (Equation 10)

        Rearranging the equation:  dq/q = -dt/RC

        The limits are now from maximum charge Q = eC to q when t goes from 0 to t. The capacitor is discharging and  I  is in the opposite direction.


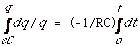
        ln q/eC = - t/RC  or
        q(t) = Qe-t/RC = eCe-t/RC                  (Equation 11)
      2. I(t) = dq/dt = -(eC/RC)e-t/RC = - (e/R)e-t/RC

      3. Vcb = VC = q/C = ee-t/RC   and   Vac = IR = -ee-t/RC

      4. Referring to Fig. 5b below,



        For decay of charge,  VC(t) = e e-t/RC.  When t = RC = 5 s,
        VC(RC) = 1.0 V(e-RC/RC ) = 1.0 V( e-1) = 1.0 V(0.368) = 0.368 V.

        For decay of charge,  VR(t) = -ee-t/RC.  When t = RC = 5 s,
        VR(RC) = -1.0 V(e-RC/RC) = -1.0 V(e-1) = -1.0 V(0.368) = -0.368 V.

    4. Sample problem in 106 Problem Set for Circuits: 10.

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
August 8, 2002
April 23, 2003