|
Outline - One Dimensional Motion
|
|
- Language of Motion
- Displacement is the change in position of an object. It
is represented by a directed line segment s. For motion
in the x or y-direction, it is represented by x or y, respectively.
- Speed is the distance traversed per unit time. The velocity
v of an object is a specification of both its speed
and the direction in which it is moving.
- The average velocity
 of
an object during a time interval t is the distance covered
during this time interval, divided by the time t. of
an object during a time interval t is the distance covered
during this time interval, divided by the time t.
- Instantaneous velocity is the velocity of an object
at any instant of time. For a case of constant velocity,
the instantaneous velocity is equal to the constant velocity
at all times.
- Acceleration a is the rate at which an object’s
velocity changes per unit time.
- The change in velocity may be in magnitude, or direction,
or both.
- For constant acceleration, the direction of the velocity
does not change and the rate of change of the velocity
is constant.
- Motion in One-Dimension
- Relations Among Descriptive Quantities
- Velocity and Displacement
- dx/dt = v. The slope of x versus t at any instant
equals the velocity at that instant
- Separating variables : dx = v dt
Integrating:
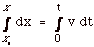
distance moved equals:
|
x
– xo =
|
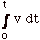 |
= area under v vs t from
t = 0 to t = t.
|
- Velocity and Acceleration
- dv/dt = a. The slope of v versus t at any instant
equals the acceleration at that instant.
- Separating variables: dv = a dt
Integrating:
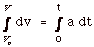
change in velocity equals:
|
v
– vo =
|
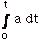 |
= area under a vs t curve
from t = 0 to t = t.
|
- For Constant Velocity v
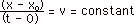
where x = position at time t and xo = position
at t = 0.
Rearranging, x function of t,
x(t) = vt + xo
(Equation2c)
compare with y function of x,
y(x) = mx + b
and see that a plot of x as a function of t gives a straight
line with the slope equal to the velocity and intercept
on the X-axis equal to xo.
- Example in Fig. 1 below with v = 2.0 m/s
- For graph 1 in Fig. 1a, xo = 1.5 m and
x(t) = (2.0 m/s)t + 1.5 m
- For graph 2 in Fig. 1a, xo = 0 and x(t)
= (2.0 m/s)t
- Velocity v as a function of time t in (Fig. 1b below).
For all times, v = 2.0 m/s. A plot of v as a function
of times gives a straight line parallel to the t-axis.
The area under the v versus t curve = vt. From t =
0 to t = 1.0 s, vt = (2.0 m/s)(1.0 s) = 2.0 m = the
distance moved. In Fig. 1a for graph 1, xo
= 1.5 m and x(t = 1 s) = xo + area under
v vs t = 1.5 m + 2.0 m = 3.5 m and x = 3.5 m at t
= 1.0 s. In Fig. 1a for graph 2, xo = 0
and x = area under v vs t = 2.0 m and x = 2.0 m at
t = 1.0 s. For all cases of constant velocity, a plot
of v as a function of time yields a straight line
parallel to the t-axis. The slope of this line is
zero.
- In Fig. 1 c above, the acceleration a is zero for
all times. The area under a versus t is zero which
corresponds to zero change in velocity. For all cases
of constant velocity, a plot of a as a function of
time yields a straight-line through the t-axis.
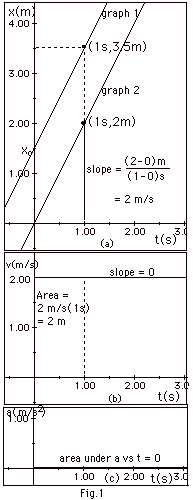
- For constant acceleration,
- a = (v - vo)/(t - 0) = a constant. (Equation
1’)
Since the slope of v as a function of time t equals the
acceleration, a plot of v versus t yields a straight line
as shown in Fig. 2 below. The area under the curve of
v versus t from t = 0 to t = t is the distance moved x
- xo.
From Fig. 2 above,
x – xo = vot
+ 1/2(v – vo)t
(Equation
2’)
Rearranging Eq. 1':
(v – vo) = at
(Equation
1”)
Substituting Eq. 1” into Eq. (2’):
x – xo = vot +
1/2 at2
(Equation
2”)
If you solve for t in Eq. 1’ and substitute it into
Eq. 2”, you find:
v2 = vo2
+ 2a(x – xo) (Equation
3)
- Important equations for motion with constant acceleration
- v(t) = vo + at (Equation
1)
Eq.1 gives velocity v at any instant as a function
of time t
- x(t) = xo + vot + 1/2 at2 (Equation
2)
Eq. 2 gives the displacement x at any instant as a
function of time t
- v2(x) = vo2 + 2a(x
- xo) (Equation
3)
Eq. 3 gives the velocity v as a function of position
x
- Example in Fig. 3 below with a = 1.0 m/s2 and
initial conditions, xo = 0 and vo
= 1.0 m/s. For this case,
- v(t) = 1.0 m/s + 1.0 m/s2 t
- x(t) = 0 + 1.0 m/s t + 1/2(1.0 m/s2)
t2
- v2(x) = (1.0 m/s)2 + 2(1.0
m/s2)(x - 0)
- acceleration a = slope of v vs t = 1 m/s2
(Fig. 3b)
- area under v versus t graph from t = 0 to t = 1,
x(1s) - x(0 s) = (0.5 +1.0)m = 1.5 m. (Fig. 3b)
x(1s) = 1.5 m + x(0 s) = 1.5 m, as in Fig. 3a
- area under a versus t graph (Fig. 3c) from t = 0
to t = 1 s,
v(1s) - v(0 s) = 1.0 m/s.
v(1s) = 1.0 m/s + vo = (1.0 + 1.0)m/s =
2 m/s (Fig. 3b)
- Slope of x vs t at t = 0 equals vo =
1.0 s. Slope of x vs t is positive and increasing
(Fig. 3a) as is the velocity (Fig 3b).

- Sample Problem. A person tosses a ball up into the air
from yo = 1.0 m with an initial velocity vo
= 6.0 m/s (Fig. 4 below). Find the height to which
the ball rises. Take g = 10 m/s2.
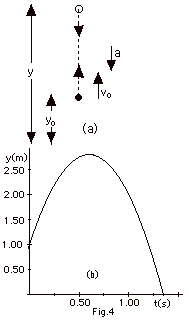
- Approach 1:
We do not know the time the ball takes to get to its
highest point or the value of y at that point. We
do know that at the highest point the ball momentarily
stops and then returns to the ground. At the highest
point, v = 0.
- For a one-dimensional problem, we can indicate
directions by a + or - sign. Choose up to be positive
so a = -10 m/s2. v(t) = vo
+ at. At the top, v= 0 and 0 = 6.0 m/s –(10
m/s2)t and t = 0.6 s.
- y(t) = yo + vot + 1/2
at2
y(0.6 s) = 1.0 m + 6.0 m/s(0.6 s) - 1/2(10 m/s2)(0.6
s)2
= 2.8 m
- Approach 2:
Use v2(y) = vo2 +
2a(y - yo) 0 = (6 m/s)2 + 2(-10
m/s2)(y - 1.0m) or (20 m/s2)(y
– 1.0m) =36 m2/s2 and
y - 1.0 m = 1.8 m
or y = 2.8 m.
- Note in Fig. 4a, I show the path of the ball as
it rises and falls. In Fig. 4b, I plot y as a function
of time t. Note Fig. 4b is NOT a path.
- Combination of Motions (Fig. 5a below)
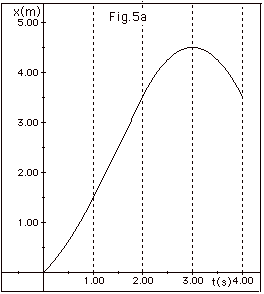
- From t = 0 to t = 1, the plot of x as a function of
time is not a straight line so this is not a case of constant
velocity. The slope is positive and increasing so the
velocity is positive and increasing.
- From t = 1 to t = 2 s, the plot of x as a function of
time is a straight line. This is a case of constant positive
velocity.
- From t = 2 to t = 3 s,the plot of x as a function of
time is not a straight line so this is not a case of constant
velocity. The slope is positive, but decreasing so the
velocity is positive and decreasing.
- At t = 3 s, the slope of x versus t is zero. The velocity
at t = 3 s is zero. From t = 3s to t = 4 s, the slope
is negative and increasing. The velocity is in the negative
X-direction and it is increasing.
- Fig. 5b below is a plot of velocity v as a function
of time t. The analysis given in 4 above agrees with the
results of this plot. We find the values of x for any
time t from the area under the v versus t curve.
As shown in Fig. 5b:
The area under v vs. t from t = 0 to t = 1 s is 1.5 m
and x(1s) = 1.5 m. The area under v vs. t from t = 0 to
t = 2 s is 3.5 m and x(2s) = 3.5 m. The area under v vs.
t from t = 0 to t = 3 s is 4.5 m and x(3s) = 4.5 m. The
area under v vs. t from t = 0 to t = 4 s is (1.5 + 2.0
+ 1.0 - 1.0)m = 3.5 m and x(4s) = 3.5
m.
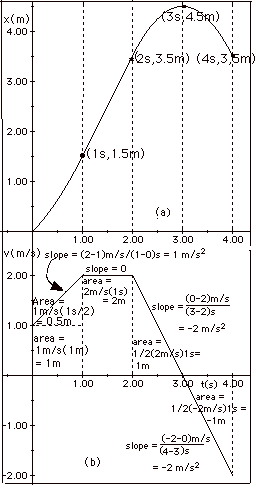
- The slopes of v versus t for the various time intervals
are given in Fig. 5b above:
From t = 0 to t = 1.0 s, dv/dt = a = 1 m/s2.
From t = 1 to t = 2.0 s, dv/dt = a = 0.
From t = 2 to t = 4.0 s, dv/dt = a = -2.0 m/s2.
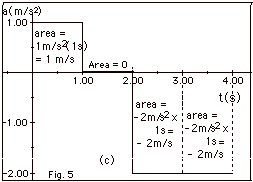
- The areas under a versus t (Fig. 5c above) gives the
change in velocity. The initial velocity was 1.0 m/s.
The change in velocity from t = 0 to t = 1.0 s is 1 m/s.
v(1s) = 1 m/s + 1 m/s = 2 m/s.
The change in velocity from t = 0 to t = 2.0 s is (1 +
0) m/s = 1 m/s.
v(2s) = 1 m/s + 1 m/s = 2 m/s.
The change in velocity from t = 0 to t = 3.0 s is (1 +
0 - 2.0)m/s
= -1 m/s. v(3s) = 1 m/s - 1 m/s = 0 m/s.
The change in velocity from t = 0 to t = 4.0 s is (1 +
0 - 2.0 - 2.0)m/s
= -3.0 m/s.
v(3s) = 1 m/s - 3 m/s = -2 m/s.
- Motion with Constant Velocity as a Special Case of Constant
Acceleration
- For constant acceleration,
- v(t) = vo + at
(Equation
1)
- x(t) = xo + vot + 1/2 at2 (Equation
2)
- v2(x) = vo2 + 2a(x
– xo) (Equation
3)
- For constant velocity a = 0 and the equations above
become
- v(t) = vo
(Equation
1c)
- x(t) = xo + vot
(Equation 2c)
- v2(x) = vo2 (Equation
3c)
Notice for v(t) = vo = constant, Equation
2c above is equivalent to Equation 2c in Section II,
B, 1 above.
- Sample problems in 107
Problem Set for One Dimensional Motion: 1-15.
- Units
- Dimensional Analysis (Units are your friends!)
- Given an object moving with a constant acceleration
a = 4.0 m/s2, an initial velocity of 5.0 m/s
and an initial position at t = 0 of 1.0 m, find its position
at t = 2.0 s.
- Let's say you make a mistake and write x(t) as
- x(t) =? xo + vot + 1/2 at
- Substitute in the values that are given with their
units
- x(2.0 s) =? 1.0 m + (5.0 m/s)(2.0 s) + 1/2(4.0 m/s2)(2.0
s)
- This gives x(2.0 s) ≠ 1.0 m + 10 m + 8 m/s
which cannot be true because m ≠ m/s
- Conversion of Units
- Change 60 miles/hour to ft/s
- 1 mile = 5280 ft or 5280 ft/1 mile = 1
- 1 hour = 3600 s or 1 hour/3600 s = 1
- You do not change a quantity if you multiply it by 1
- Thus 60 mile/hour x 5280 ft/mile x 1 hour/3600 s =
60(5280/3600) ft/s = 88 ft/s. Notice I have arranged the
quantities equal to 1 so that the units of miles and hour
cancel.
|
|