|
|
- Angular Motion
- Angle in radians
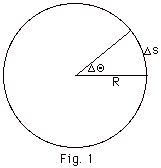
- An angle in radians is defined as the arc it subtends
divided by the radius of the circle. In Fig. 1 below,
the angle is ΔΘ, the arc it subtends is Δs,
and the radius is R. ΔΘ = Δs/R Notice that
the unit of Δs is meters and the unit of R is meters
so the angle has no unit. We say radians or degrees
to imply in which we are measuring the angle.
- Conversion of radians to degrees or degrees to radians
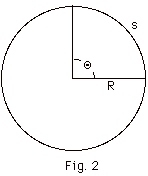
- The circumference of a circle equals 2 πR.
In Fig. 2 below, s equals one-quarter of a circle
or s = 2 πR/4 = πR/2. In radians the angle
= s/R = ( πR/2)/R = π/2. In Fig. 2, Θ
= 90o. Thus π/2 radians = 90o
or π radians = 180o.
- In general, (angle in radians)/(angle in degrees)
= π/180.
- Descriptive Terms
- Speed v at any point = the magnitude of thevelocity
tangent to the path at that point.
- For circular motion the Period T = time for one complete
rotation = 2 πr/v
- The frequency f = reciprocal of period = 1/T = v/2 πr
- The angular velocity ω (omega not w) = the angle
turned through per second or for a varying angular velocity
= dΘ/dt. In Fig. 1 above,
ΔΘ = (1/R)( Δs)
(Equation
#1)
Dividing both sides of Equation #1 by Δt,
ΔΘ/ Δt = (1/R)( Δs/ Δt)
(Equation
#2)
Taking the limit of both sides of Equation # 2 as t approaches
zero gives dΘ/dt = (1/R) ds/dt.
Recognizing dΘ/dt as the angular velocity ω
and ds/dt as the linear velocity v gives us the relation
between ωand v. ω = v/R.
Since the frequency f = v/2 πR or v = 2 πRf,
ω = (2 πRf)/R = 2 πf
- Alternative expressions for centripetal or radial acceleration,
- ar = v2/R
- ar = (2 πR/T)2/R = 4
π2R/T2 = (2 πRf)2/R
= (2 πf)2R = ω2R
- Angular acceleration α is the rate of change of
angular velocity.
α = dω/dt. Its unit is s-2.
| For constant
angular acceleration
|
Linear analogy |
| ω(t)
= ω0 + ατ |
v(t)
= vo + at |
| Θ(t)
= Θ0 + ωt + 1/2 αt2 |
x(t) = x0
+ v0t + 1/2 at2 |
| ω2(Θ)
= ωo2 + 2α(Θ
- Θo) |
v2(x)
= vo2 + 2a(x – xo) |
- Sample Problems in 104
Problem Set for Angular Motion: 4-7.
- Rigid Body
- All points on the object rotate with the same angular
velocity ω.
- For every mass m1, m2 m3,
etc. that makes up the body, v1 = ωr1,
v2 = ωr2, v3 = ωr3,
etc. (See Fig. 3 below)
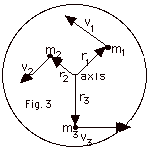
- K = 1/2 m1v12 + 1/2 m2v22
+ 1/2 m3v32 + + + +
= 1NΣ (1/2) mivi2K
= 1/2 m1r12ω2 +
1/2 m2r22ω2
+ 1/2 m3r32ω2
+ + +
= 1NΣ (1/2) miri2ω2
- Define Moment of inertia I = 1NΣ
miri2. Then
K = (1/2)Iω2.
- Compare with K = 1/2 mv2 for translation
-
If distribution of mass is continuous then integrate
to find moment of inertia
I=∫dm
r2
- Moments of Inertia
- Hoop (Fig. 4a below) All points on the hoop equal the distance
R from the axis of rotation. The moment of inertia of a hoop
about its center of mass = MR2.
- Circular Disk (Fig. 4b above) Now there is mass spread throughout
the object. The moment of inertia of a disk about its center
of mass is 1/2 MR2, smaller than that for a hoop
because some of its mass is closer to the center of the disk
and r for those masses is less than the radius R of the disk
- A cylinder can be considered a series of disks. The moment
of inertia of a cylinder about its center of mass =1/2 MR2.
- The moment of inertia of a sphere about its center of mass
I = 2/5 MR2.
- Thin Rod
- Moment of Inertia about center of mass = ML2
/12
- Moment of Inertia about one end = ML2/3
- (Fig. 5 below) Parallel Axis theorem: I(parallel) = I(CenterMass)
+ Md2, where d is the distance between the axes.
Example: Thin rod about one end. I = ML2/12
+ M(L2/4) = ML2/3
- Sample Problems in 104
Problem Set for Angular Motion: 8, 9.
- Application of Conservation of Energy to Rotation
Object of mass M, radius R and moment of inertia ICMis
initially at rest at the top of an incline. The distance between
the center of the object at the top of the incline and at the
bottom of the incline is h (Fig. 6 below).
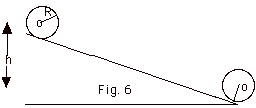
It rolls without slipping down the incline. A frictional force
acts on the object, but the frictional force acts at a point,
not through a distance so the frictional force does no work and
we can use conservation of energy to solve this problem.
1) At the top, Etop = U + K = Mgh
+ 0
2) At the bottom since the sphere has both translational
and rotational kinetic energy, Ebottom = U + K = 0
+ (1/2 Mv2 + 1/2 ICMω2)
3) Since ω = v/R, Ebottom =
1/2 Mv2 + 1/2 ICM(v2/R2)
4) From conservation of energy, Mgh = 1/2 Mv2
+ 1/2 (ICM/R2)v2or v2
= 2gh/(1 + ICM/MR2)
Special Cases:
a. For hoop, ICM = MR2,
v = (gh)1/2
b. For disk or cylinder, ICM = MR2/2,
v = (4gh/3)1/2
c. For sphere, ICM = 2MR2/5,
v = (10gh/7)1/2
- Work Done on Rotating Rigid Body
- Since ω2 = ωo2
+ 2α(Θ - Θo), 1/2 ICM ω2
- 1/2 ICM ωo2
=
ICMα(Θ - Θo).
- Identify the left-hand side of the above equation as ΔK
and the right hand side as the work W = ICMα(Θ
- Θo).
- Sample Problems in 104
Problem Set for Angular Motion: 11-13.
- Torque τ (Fig. 7 below)
- τ= r x F
- Magnitude of τ = rF sin r,F =
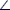 (r
sin r,F (r
sin r,F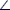 )F= )F=
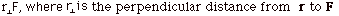
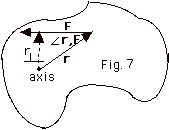
- Direction of torque. For τ= r x F,
point the fingers of your right hand in the direction of r
with the palm of your hand ready to rotate in to F.
Rotate your fingers into F. The thumb of your right
hand points out of the page. The torque τ is out
of the page (Figure 7a below).
- Sample Problems in 104
Problem Set for Angular Motion: 10, 14, 15.
- Angular Momentum L
- For a point particle of mass m moving with velocity v,
L = r x mv, where r is the distance from the
axis to the position of the mass m.
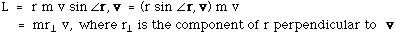
- For direction of L, point the fingers of your right
hand in the direction of r and rotate your fingers
into the direction of v, your thumb and the angular
momentum L point out of the page (Fig. 8 below).
- For a rotating rigid body L = Iω. The
direction ofωis found by curling the fingers of
your right hand in the direction of the rotation. Your thumb
points to the direction of ω and for a rotating
rigid body to the direction of L.
- For point object, dL/dt = d(r x mv)/dt
= d(r)/dt x mv + r x d(mv)/dt
= [v x mv]+ r x d(mv)/dt = 0 +
r x F, because [v x v] = 0 and
F = d(mv)/dt. Thus dL/dt = r x
F = t . When the torque equals zero,
the angular momentum remains constant. When no external
torque acts on a system, angular momentum is conserved.
- For rotating rigid body,
- τ = dL/dt = d(Iω)/dt = Iα
- Work = W = (Iα)Θ = τΘ
- Conservation of Angular Momentum1. If no net external torque
acts on a system, its total angular momentum L remains constant.
τ= dL/dt. If τ =
0, dL/dt = 0 and L remains constant.
Examples:
- Person on rotating table
- Planetary motion
- Gyroscope
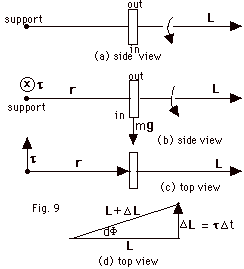
- Wheel spins clockwise as viewed from support (Fig.
9a below).
L is to the right.
- The torque due to the weight mg is τ
= r x mg points into the paper (Fig.
9b below).
- As seen from above L precesses slowly counter-clockwise
(Fig. 9 c and d below). L + ΔL =
L + τ Δt, where τ
= dL/dt.
- dΦ = τ dt/L or Ω = dΦ/dt = τ
/L = mgr/Iω.
Wheel spins at rate ω and precesses at rate Ω.
- d(L2)/dt = d(L . L)/dt
= L . dL/dt + L .
dL/dt = 2L . dL/dt
= 2L . τ
= 2Lτ cos L
L
τ =2Lτ cos 90o = 0.
Since τ is perpendicular to L, there is
no change in the magnitude of L, only change is in its direction.
- Sample Problems in 104
Problem Set for Angular Motion: 16, 18-20.
- Example. A piece of playground apparatus consists of two carts,
each of mass 50 kg, that are joined by very light (compared to
the mass of the carts) rigid rods, 2 m each in length, as shown
in Fig. 10 below.
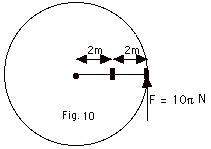
To make this device rotate, a child applies a constant force of
10 π N to the outer cart, directed perpendicular to the rods.
The apparatus is initially at rest. Find:
- the moment of inertia of the apparatus
- the angular acceleration produced by the child
- how long it will take for the apparatus to make one complete
revolution
- at the time for (c), the angular velocity and the kinetic
energy of the apparatus, and
- the work done by the child.
- Find the direction and magnitude of ΔL/ Δt and
the torque
- Solutions:
- Treating the two carts as point particles,
I = 50 kg(2 m)2 + (50 kg)(4 m)2 =
1000 kg-m2.
- τ = r x F.
τ = (4 m)(10 π N) sin 90o = 40 π
N-m = Iα = 1000 kg-m2α.
α = 0.04 π s-1
- Angle turned through in one complete revolution =
2 π = 1/2 αt2T = [(4 π)/α]1/2
= [(4 π)/4 π x 10-2 s-2]1/2
= 10 s
- angular velocity:
ω = ωo + αt
= 0 + (4 π x 10-2 s-2)(10 s)
= 0.4 π s-1
kinetic energy:
K = 1/2 Iω2 = 1/2 (1000
kg-m2)(0.4 π s-1)2
= 80 π2 J
- W = τΘ = (40 π N-m)( 2 π) = 80 π2
J = Kf – KI = 80 π2
J – 0
- Since ωo = 0, Lo = 0. Final
L = Iω. Since the apparatus rotates counterclockwise,
ω is out of the page. After one revolution,
L = (1000 kg-m2)(0.4 π s-1) =
4 π x 102 m-kg/s ΔL/ Δt
= (4 π x 102 m-kg/s)/(10 s) = 40 π
m-kg/s2 = τ out of page
- Combination of Translational and Rotational Motion (Fig. 11
below)
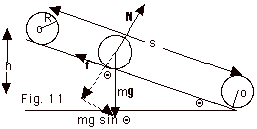
For a sphere to roll without slipping down the incline plane there
must be a frictional force f. We need two equations of
motion, one for translation and one for rotation.
For translation:
Fnet = ma
mg sin Θ - f = ma
For rotation about the center of mass, neither N nor mg
produces a torque about the center of mass because their line
of actions pass through the center of mass. Thus:
τCM = ICMα
fR sin 900 = (2/5 mR2)ω or since α
= a/R, f = 2/5 ma
Substituting the second equation into the first:
mg sin Θ - 2/5 ma = ma or a = 5g sinΘ/7v2
= v02 + 2as = 0 + (10/7)g(s sinΘ) =
(10/7)gh, v = (10gh/h)1/2
as we found before using conservation of energy.
- Conditions for Equilibrium
- The sum of the external forces must be zero, or
Σ F = 0
- The sum of the external torques must be zero, or
Στ = 0
- Example (Fig. 12a below):
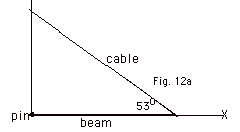
A uniform horizontal beam of length 8.00 m and weight 200
N is attached to a wall by a pin connection. Its far end is
supported by a cable that makes an angle of 53.0o
with the horizontal. If a 600-N person stands 2.00 m
from the wall, find the tension in the cable and the force
exerted by the wall on the beam.
- Solution to Example (Fig. 12b below):
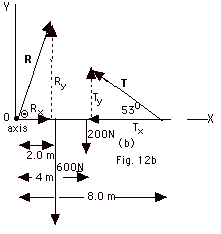
- The forces acting on the beam are:
- The gravitational force of the earth on the beam,
its weight = 200 N acts at the center of the uniform
beam.
- The force of the man on the beam = 600 N
- The tension T in the rope
- The force R exerted by the wall at the pivot
- The torques acting on the beam about the axis at the
pivot point are:
- Torque due to R is zero because it acts at the
pivot point. Any force that passes through the axis
produces no torque (r = 0).
Note:
I chose the axis at the pivot point to eliminate one
of the unknowns in the torque equation, leaving only
T as an unknown.
- The torque due to the tension in the rope = 8.0
m(T) sin 53o
out of the page.
- The torque due to the force of the man = 2.0 m(600
N)
into the page
- Since it is a uniform beam, the weight of the beam
acts at the center.
r = 4 m for the beam weight.
Torque = 4.0 m(200 N) into the page.
- Σ τ = 0
Taking out of the page as positive:
+8.0 m(T) sin 53o - 2.0 m(600
N) - 4.0 m(200 N) = 0
8.0 m(T)(0.80) = 2000 N-m. T
= 313 N
- The vector sum of the forces must = 0.
Change this two-dimensional problem into two one-dimensional
problems, by taking the components of the tension T
and the force of the wall at the pivot R into X
and Y components.
As shown in Fig. 12b,
Tx = T cos 53o
Ty = T sin 53o,
Rx = R cos Θ, and
Ry = R sin Θ
| ΣFx
= 0 |
ΣFy
= 0 |
| R cos Θ -
T cos 53o = 0 |
R sin Θ +
T sin 53o – 600N – 200N =
0 |
| R cos Θ =
T cos 53o |
R sin Θ =
- T sin 53o + 600 N + 200 N |
| R cos Θ =
313(0.6) |
R sin Θ=
-313 N(0.8) + 800 N |
| R cos Θ =
188 N (Equation
1) |
R sin Θ=
550 N (Equation
2) |
Dividing Eq.2 by Eq. 1:
tan Θ= 550
N/188 N = 2.92. Θ = 71.10
R.
R sin Θ= 550 N.
R = 550 N/sin Θ.
R = 550 N/sin 71.1o = 581 N.
- Sample Problems in 104
Problem Set for Angular Motion: 22-24.
- Using Cross Product with Unit Vectors
- Definitions
- Magnitude of C = A
x B is C = |A||B|cos
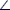 A,
B. A,
B.
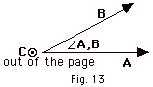
- Point the fingers of your
right hand in the direction of A with your palm
toward B. Rotate your palm into B.
Your thumb points in the direction of C. In
Fig. 13 below, C is out of the page.
- Application to unit vectors
- i x i = |i||i|sin
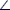 i,
i = |1||1|sin 0o
= 0 i,
i = |1||1|sin 0o
= 0
j x j = |j||j|sin 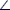 j,
j = |1||1|sin 0o
= 0 j,
j = |1||1|sin 0o
= 0
k x k = |k||k|sin 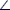 k,
k = |1|1|sin 0o = 0 k,
k = |1|1|sin 0o = 0
- Magnitudes and Directions
- Magnitude: |i
x j| = |i||j|sin
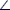 i,
j = |1||1|sin 90o
= 1 = |j x i| i,
j = |1||1|sin 90o
= 1 = |j x i|
Direction: i x j = k
j x i = - k
- Magnitude: |i
x k| = |i||k|sin
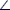 i,
k = |1||1|sin 90o
= 1 = |k x i| i,
k = |1||1|sin 90o
= 1 = |k x i|
Direction: i x k =- j k
x i =j
- Magnitude: |j
x k| = |j||k|sin
 j,
k = |1||1|sin 90o
= 1 = |k • j| Direction: j
x k = i k x
j = - I j,
k = |1||1|sin 90o
= 1 = |k • j| Direction: j
x k = i k x
j = - I
|
|