Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 106

Outline - Electric Fields
  1. Difference between Action-at-a-Distance and Field Approach

    1. Action-at-a-Distance (Fig. 1a)



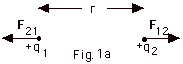
      1. Assume one charge acts through a distance to exert a force on another charge.

      2. The force F21 of q2 on q1 is equal in magnitude to
        the force F12 of q1 on q2,  but is opposite in direction.

        Fe = F21 = F12 = q1q2/4πεor2 = kq1q2/r2,
        where 1/4πεo = k = 9.0 x 109 N-m2/C2.

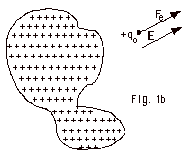
    2. In the electric field approach (Fig. 1b below), the electric field associated with a charged object permeates all of space. It is then the electric field that exerts a force on another charge placed in this field. The electric field at a point P equals the electric force Fe on a positive point charge qo divided by qo. The direction of the electric field is that in which a positive test charge is urged.




  2. Finding Electric Fields

    1. In general the electric field E = Electric force Fe on qo divided by qo.

      For the special case of an electric field due to a point charge +Q
      at a distance r from +Q =
      E = (Fe on qo)/qo = (kQqo/r2)/qo = kQ/r2.
      Notice the electric field at P depends on the charge Q that sets up the field and the distance of P from Q, but it does not depend on the test charge.
      See Fig. 2a below.



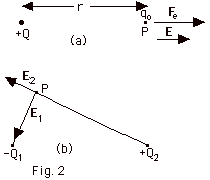
      If the electric field is due to more than one charge (Fig. 2b above), find the electric field at P due to each charge. The resultant field equals the vector sum of the fields due to each individual charge (Fig. 2b above).

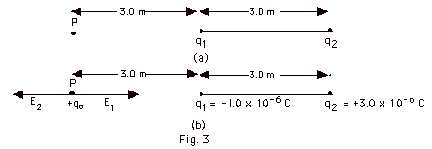
      Sample Problem:  In Fig. 3,  q1 = -1.0 x 10-6 C and q2= +3.0 x 10-6 C.
      Find the electric field at point P in Fig. 3a below.



      Solution to Sample Problem: The electric field due to a point charge q = kq/r2, where q is the charge setting up the field and r is the distance of the point P at which you wish to find the field from q. The direction of the electric field is that in which a positive test charge +qo is urged. Think of the charges setting up the field as set in concrete. You are not interested in a force between the charges and what happens to these charges when you are finding the field due to them.

      The electric field due to q1=

      E1 = (9.0 x 109 N-m2/C2)(1.0 x 10-6 C)/(3.0 m)2 = 1.0 x 103 N/C.

      Do not put in the minus sign for the charge. Look at the figure and imagine a positive test charge qo at P.  q1 would attract the positive test charge, so E1 is to the right.

      The electric field due to q2 =

      E2 = (9.0 x 109 N-m2/C2)(3.0 x 10-6 C)/(6.0 m)2 = 0.75 x 103 N/C.

      q2 would repel the positive test charge, so E2 is to the left. The field due to both charges E = (1.0 - 0.75)103 N/C = 0.25 x 103 N/C to the right.

    2. When you have a "continuous" distribution of charge, you may think of the total charge as made up of elements of charge dq.  For a line of charge, it is useful to define  λ = charge/length. Then the charge element  dq = λ(element of length). For a line of charge, take the element of length = dx.  Then dq = λdx.  If the distribution of charge is along an arc,  the element of length is  ds  and  ds = R dΘ with dq = λRdΘ.

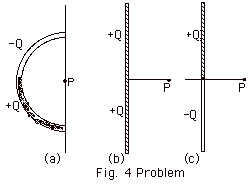
      Sample Problem: In Fig. 4 below, there are three nonconducting rods, one circular and two straight. Each has a uniform charge of magnitude Q along its top half and along its bottom half. Find the direction of the resultant electric field at point P for each of the rods.



      Solution of Sample Problem: For each case I took distributions of charge that were symmetrically distributed about the center of the rod. I also took equal quantities of charge dq.  At point P in Fig. 4a, the electric fields due to a negative and positive element of charge dq are as shown in the Solution Figure below:



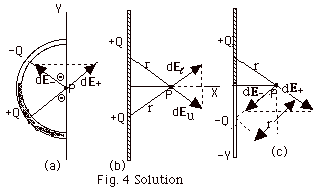
      Remember that the direction of an electric field is the direction in which a positive test charge is urged.  At P, the -dq on the upper arc of the rod would urge the test charge toward it, while the +dq on the lower arc would urge the test charge away from it. Notice that the components of  dE+  and  dE-  in the X-direction cancel. Since this is true for all of the symmetrically disposed elements, the resultant field is in the +Y-direction. In (b) the  +dq symmetrically disposed elements (the distance r from each element is the same) urge a positive test charge away from them. Since this is true for all of the symmetrically disposed elements, the components in the Y-direction cancel and the resultant electric field is in the +X-direction. By similar reasoning you can see that the resultant electric field in (c) is in the - Y-direction.

    3. Additional sample problems are found in 106 Problem Set for Electric Fields: 1 - 5, 7, and 8.



  3. Electric Flux ΦE

     Definition: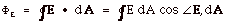
    where E, dA equals the angle between E and dA.  dA is an element of area.
    The direction of dA is that of the outward normal to the surface.




  4. Gauss's Theorem



    2. ΦE is the total flux crossing a three dimensional surface

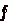    3. is the integral around a closed three dimensional surface

    4. Application

      Choose Gaussian surface that gives maximum symmetry properties such that:

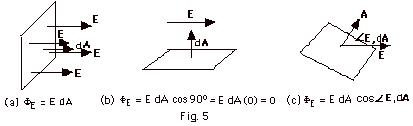
      1. E is normal to the surface, that is, the angle between E and dA
        is zero, and E . dA = E dA cos 0o = E dA

      2. E is constant everywhere on the surface, that is,

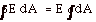
    5. Examples

      Spherically symmetrical distribution of charge (Fig. 6 below):



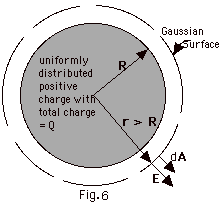
      1. For hypothetical Gaussian surfaces (shown by dashed cross-section of spheres in Fig. 6) choose sphere.

      2. E must be normal to surface and constant at any point on a Gaussian surface or the symmetry of a sphere would be unraveled by rotating it.

        1. For  r > R  or  r < R,   E, dA must be zero and E is constant everywhere on the Gaussian surface.





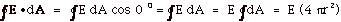
        2. For r ≥ R,  E(4 πr2) = Q/ εo or E = Q/4πεor2

        3. For r ≥ R,  all the charge acts as though it were a point charge at the center of the sphere.


  5. Electric fields due to other special cases

    1. Electric field due to an infinite plane = 2 πkq/A = σ/2 εo,  where q is the charge on the plate,  A the area of the plate,  σ the charge per unit area = q/A,   k = 9.0 x 109 N-m2/C2,  and 1/ ε0 = 4 πk.

    2. Electric field between two oppositely charged plates = 4 πkq/A = σ/ ε0.

    3. Electric field due to long line of charge or outside a cylinder of charge is λ/2πεor = 2k λ/r  where  λ= charge per unit length = q/L.

    4. Electric field due to a conducting sphere with radius R and charge Q outside of the sphere is Q/4πεor2 = kQ/r2.


  6. Electric Field inside a Conductor

    1. A conductor is defined as a material in which electrons are free to move. They move until there is no electric field inside the conductor.



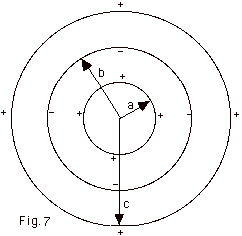
    2. Figure 7 above represents a conducting sphere of radius a coaxial with a conducting spherical shell of inner radius b and outer radius c.

      1. If positive charge q is placed inside the sphere, electrons move in such a way to make the electric field inside the sphere equal to zero and the positive charge +q on the outside of the conducting sphere.
         
      2. Electrons from the spherical conducting shell are drawn towards the positive charge on the sphere, leaving the inner surface of the shell with a negative charge -q, the outer surface of the conducting spherical shell positively charge +q and no electric field inside the conducting shell.

    3. Sample problems in 106 Problem Set for Electric Fields: 9, and 11-15.


  7. Electric Field of a Dipole



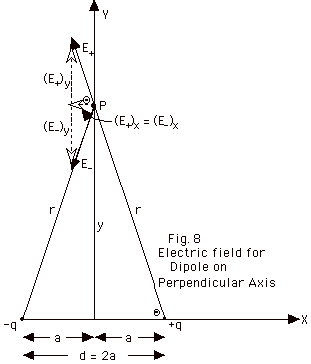
    1. Description

      1. Dipole consists of two point charges of opposite sign, but equivalent quantity of charge.

      2. The charges are separated by a distance d = 2a in Fig. 8 above.

      3. We are often interested in cases for which the distance from the center of the dipole to the point P where we wish to find the electric field is much greater than d the distance of separation of the charges.

    2. Calculation of E for point on perpendicular bisector (Fig. 8 above)

      1. At P, the electric field due to the positive charge is
        E+ = kq/r2 = kq/(a2 + y2)
        upward along the line connecting P with
        +q.

      2. At P, the electric field due to the negative charge is
        E- = kq/r2 = kq/(a2 + y2)
        downward along the line connecting P with
        - q.

      3. Notice that the magnitudes of the field due to +q and - q are equal.
        In Fig. 8, we see the Y-components of the electric field due to +q and the electric field due to - q,  (E+)y and (E-)y , respectively, cancel.

      4. The components of the electric field in the X-direction,
        (E+)x = E+ cos Θ  and  (E-)x = E- cos Θ are equal because E+ = E-. These components are in the same direction so they add. The total electric field at P due to both charges E = 2[kq/(a2 + y2)] cos Θ.

        From the figure, we see that cos Θ = a/(a2 + y2)1/2,
        so E = k(2qa)/(a2 + y2)3/2.

      5. For y >> a,  E = k(2qa)/y3 = k(qd)/y3 = kp/y3, where p is called the dipole moment. We can make p a vector quantity by taking its direction from the minus charge to the positive charge. The direction of the electric field in Fig. 8 is in the negative X-direction, so we may write for y >> a,  E = - kpi/y3.

    3. Calculation for electric field on axis of dipole (Fig. 9 below)



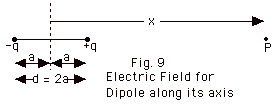
      1. Electric field at P due to - q is kq/(x + a)2 to the left.

      2. Electric field at P due to +q is kq/(x - a)2 to the right.

      3. Taking to the right to be positive, the total electric field at P due to both charges is
        E = kq[1/(x - a)2 - 1/(x + a)2]
           = kq{(x + a)2 - (x - a)2}/(x2 - a2)2
           = kq{x2 +2ax + a2 - x2 +2ax - a2}}/(x2 - a2)2
            = k4aqx/(x2 - a2)2
            = 2kpx/(x2 - a2)2.
        For x >> a,  E = 2kp/x3  and  E = 2kpi/x3.

        Again for great distances, E is inversely proportional to the cube of the distance from the center of the dipole.

    4. Sample problem in 106 Problem Set for Electric Fields: 23


  8. Force on a charged particle in a known electric field E.

    1. Once you know the electric field at a point you can find the force on a charged particle  q  placed at that point. The electric force equals the charge times the electric field. If the charge is positive, the force is in the direction of the electric field and we may write  F = qE.  If the charge is negative, the force is in the opposite direction to the field.

    2. Sample problems in 106 Problem Set for Electric Fields, 17-22.


  9. Torque on a dipole in an Electric Field

    1. Dipole moment p = qd. The direction of p is from the minus charge to the plus charge.

    2. In a constant electric field, the force on the positive charge F+ = qE to the right and the force on the negative charge F- = qE to the left.
      (See Fig. 10 below).



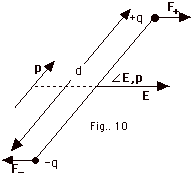
    3. The torque due to  F+  about an axis through a point half way between the charges is (qEd/2) sin E, p into the page. The torque due to  F-  is also (qEd/2) sin E, p into the page.

      The total torque = (qd)E sin E, p into the page.  A convenient way of writing the torque is τ = p x E.

    4. Sample problem in 106 Problem Set for Electric Fields: 24.

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
August 8, 2002
April 22, 2003